机器学习之牛顿法

泰勒公式

首先看泰勒公式，对于函数，如果函数平滑且某点存在各阶导数，则可以用一个多项式来描述该点邻域的近似值。公式如下：

牛顿法

牛顿法一般用来求解方程的根和求解极值。

数值优化算法除了梯度下降法外还有比较常用的一种方法是牛顿法。对于非线性方程，可以用牛顿迭代法进行求解，它收敛速度快。

基本思想是：对于非线性函数f(x)，根据泰勒公式得到x附近某个点$x_{k}$展开的多项式可用来近似函数f(x)的值，该多项式对应的函数为F(x)，求得F(x)的极小值作为新的迭代点，然后继续在新的迭代点泰勒公式展开，直到求得的极小值满足一定的精度。

原理

假设函数f(x)二次可微，则二次泰勒展开，

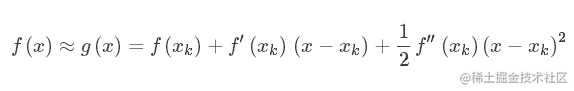
g(x)多项式则为f(x)的近似，求函数f(x)极值则可以转化为求导函数为0，对g(x)求导并令其为0，

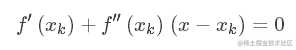
得到，

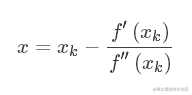
即得到迭代公式，

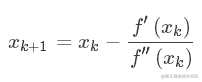
新的点$x_{k+1}$不断逼近极值，直到一次导数小于某误差。

迭代步骤

实现代码

def h(x):
    return x*x*x + 2*x*x +3*x + 4

def h1(x):
    return 3*x*x + 4*x + 3

def h2(x):
    return 6*x + 4

xk = 0
k = 1
y = 0
e = 0.0001
times = 10000

while k < times:
    y = h(xk)
    a = h1(xk)
    if abs(a) <= e:
        break
    b = h2(xk)
    xk -= a/b
    k += +1
print("k = ", k) print("x = ", xk) print("y = ", y)

以下是广告

========广告时间========

鄙人的新书《Tomcat内核设计剖析》已经在京东销售了，有需要的朋友可以到 item.jd.com/12185360.ht… 进行预定。感谢各位朋友。

为什么写《Tomcat内核设计剖析》

=========================

欢迎关注：