前端算法实战-利用贪心递归切蛋糕的小栗子

前言

本篇文章重点分享解决问题的思想，描述业务是真实项目遇到问题，为了简单明了侧重算法思想，会抛去一些业务介绍，重注思想。下面我们一起看一看这个小栗子吧！

背景

在项目中遇到了这样的问题，在电子表格中存在隐藏行和合并单元格这两个概念，当和合并单元格包含在隐藏行的单元格时，就会出问题。例如，因为做隐藏行，会把隐藏行的单元格display: none,如果合并单元格被隐藏，会导致这个合并单元格消失，致使占位空间出问题，最终表格展示不正确。

场景分析

经过沟通思考，决定在数据层处理这个问题，思路如下：

• 如果合并单元格冲突，就对这个单元格重新规划
• 隐藏行就像一把刀，对合并单元格进行切割
• 一个包含隐藏行的单元格最终被切割N个不包含隐藏行的单元格

图一：

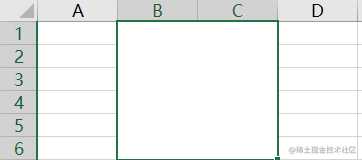
图二：

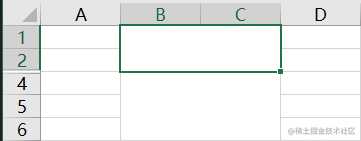
图三：

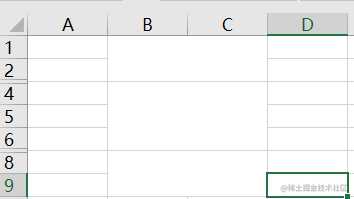
算法思路

代码含义：

• hiddenRows: 隐藏行索引号
• mergeCells: 原始合并的单元格
• row: 行索引
• rowspan: 行合并跨度

    // 隐藏行
    let hiddenRows = [0, 1];
    // 合并单元格
    let mergeCells = [{
        col: 3,
        colspan: 3,
        row: 2,
        rowspan: 1
    },{
        col: 1,
        colspan: 2 
        row: 0,
        rowspan: 4
    }]

逻辑思考

做一个最简单的假设

• 假设合并只包含一个隐藏行
• 根据隐藏行号把合并单元格一份为二

可能存在多个隐藏行，数目不确定

• 循环、遍历，递归

先贪心一下

• 保证能先得到一个不包含隐藏的合并单元格(单元格)
• 把一个大蛋糕不断的缩小

经过上述的思考，最终得到下面的代码（操作数据）

代码

// 隐藏行
let hiddenRows = [3, 6];
// 合并单元格
let mergeCells = [{
    col: 1,
    colspan: 2,
    row: 0,
    rowspan: 8
}]
let newMergeCells = [];
// 处理合并单元格，判断是否合理，不合理进行切割处理
function handleMergeCell(mergeCell) {
    let canMerge = true;
    let hiddenIndex = 0;
    let { row, rowspan } = mergeCell;
    for (let i = row; i < row + rowspan; i++) {
        if (hiddenRows.includes(i)) {
            if (canMerge) hiddenIndex = i;
            canMerge = false;
        }
    }
    canMerge && newMergeCells.push(mergeCell);
    canMerge || cuttingMergeCell(mergeCell, hiddenIndex);
}
// 切割合并单元格，保证mergeCellsTop没有问题，mergeCellsBottom再进行判断处理
// mergeCellsTop.rowspan > 0 和 mergeCellsBottom.rowspan为边界
function cuttingMergeCell(mergeCell, hiddenIndex) {
    let { row, col, rowspan, colspan } = mergeCell;
    let mergeCellsTop = {
        col,
        colspan,
        row,
        rowspan: hiddenIndex - row - 1
    };
    mergeCellsTop.rowspan > 0 && newMergeCells.push(mergeCellsTop);
    let mergeCellsBottom = {
        col,
        colspan,
        row: hiddenIndex + 1,
        rowspan: row + rowspan - hiddenIndex - 1,
    }
    mergeCellsBottom.rowspan > 0 && handleMergeCell(mergeCellsBottom);
}
mergeCells.forEach((item) => {
    handleMergeCell(item)
});
console.log(newMergeCells);

执行结果

执行代码，预期应该是2🔪切出3份

// 隐藏行
let hiddenRows = [3, 6];
// 合并单元格
let mergeCells = [{
    col: 1,
    colspan: 2,
    row: 0,
    rowspan: 8
}]

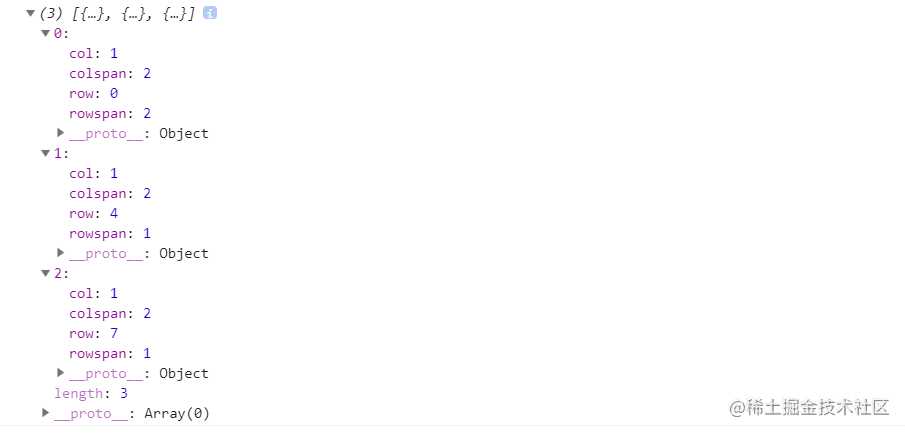
测试

jest

我们可以使用jest框架，做一些多场景的测试，来保证代码质量

测试代码

modify.js

export default {
    modifyMerageCells(hiddenRows, mergeCells) {
        let newMergeCells = [];
        // 处理合并单元格，判断是否合理，不合理进行切割处理
        function handleMergeCell(mergeCell) {
            let canMerge = true;
            let hiddenIndex = 0;
            let { row, rowspan } = mergeCell;
            for (let i = row; i < row + rowspan; i++) {
                if (hiddenRows.includes(i)) {
                    if (canMerge) hiddenIndex = i;
                    canMerge = false;
                }
            }
            canMerge && newMergeCells.push(mergeCell);
            canMerge || cuttingMergeCell(mergeCell, hiddenIndex);
        }
        // 切割合并单元格，保证mergeCellsTop没有问题，mergeCellsBottom再进行判断处理
        // mergeCellsTop.rowspan > 0 和 mergeCellsBottom.rowspan为边界
        function cuttingMergeCell(mergeCell, hiddenIndex) {
            let { row, col, rowspan, colspan } = mergeCell;
            let mergeCellsTop = {
                col,
                colspan,
                row,
                rowspan: hiddenIndex - row
            };
            mergeCellsTop.rowspan > 0 && newMergeCells.push(mergeCellsTop);
            let mergeCellsBottom = {
                col,
                colspan,
                row: hiddenIndex + 1,
                rowspan:row + rowspan - hiddenIndex - 1
            }
            mergeCellsBottom.rowspan > 0 && handleMergeCell(mergeCellsBottom);
        }
        mergeCells.forEach((item) => {
            handleMergeCell(item)
        });
        return newMergeCells
    }
}

modify.test

import modify  from '../src/modify';


test('modifyMerageCells测试1', () => {
  expect(modify.modifyMerageCells([0], [{
    col: 1,
    colspan: 2,
    row: 0,
    rowspan: 8
  }])).toEqual([{
    col: 1,
    colspan: 2,
    row: 1,
    rowspan: 7
  }]);
})

test('modifyMerageCells测试2', () => {
  expect(modify.modifyMerageCells([0, 1], [{
    col: 1,
    colspan: 2,
    row: 0,
    rowspan: 8
  }])).toEqual([{
    col: 1,
    colspan: 2,
    row: 2,
    rowspan: 6
  }]);
})

test('modifyMerageCells测试3', () => {
  expect(modify.modifyMerageCells([0, 1, 2], [{
    col: 1,
    colspan: 2,
    row: 0,
    rowspan: 8
  }])).toEqual([{
    col: 1,
    colspan: 2,
    row: 3,
    rowspan: 5
  }]);
})


test('modifyMerageCells测试4', () => {
  expect(modify.modifyMerageCells([1], [{
    col: 1,
    colspan: 2,
    row: 0,
    rowspan: 8
  }])).toEqual([{
    col: 1,
    colspan: 2,
    row: 0,
    rowspan: 1
  },{
    col: 1,
    colspan: 2,
    row: 2,
    rowspan: 6
  }]);
})


test('modifyMerageCells测试5', () => {
  expect(modify.modifyMerageCells([3], [{
    col: 1,
    colspan: 2,
    row: 0,
    rowspan: 8
  }])).toEqual([{
    col: 1,
    colspan: 2,
    row: 0,
    rowspan: 3
  }, {
    col: 1,
    colspan: 2,
    row: 4,
    rowspan: 4
  }]);
})

test('modifyMerageCells测试6', () => {
  expect(modify.modifyMerageCells([3, 5], [{
    col: 1,
    colspan: 2,
    row: 0,
    rowspan: 8
  }])).toEqual([{
    col: 1,
    colspan: 2,
    row: 0,
    rowspan: 3
  }, {
    col: 1,
    colspan: 2,
    row: 4,
    rowspan: 1
  }, {
    col: 1,
    colspan: 2,
    row: 6,
    rowspan: 2
  }]);
})

测试结果

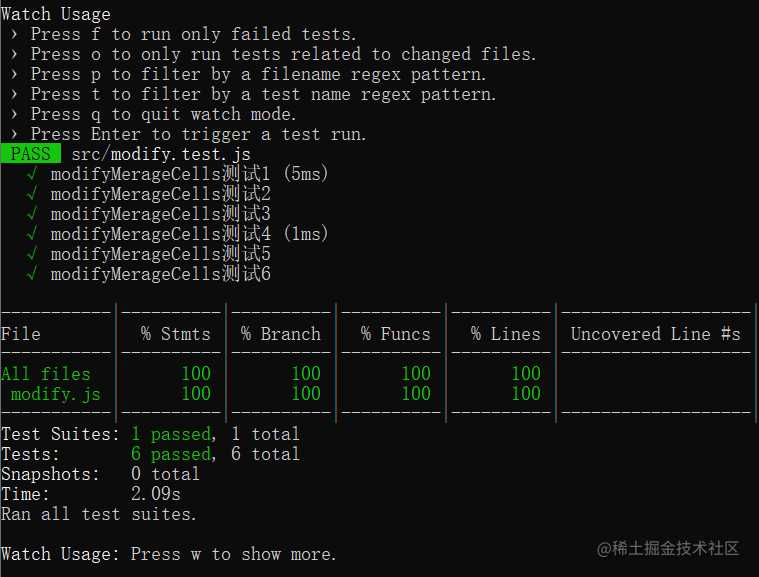
优化

这小算法写道这里还不算完事，我们可以进一步进行思考，通过空间复杂度和时间复杂度的角度进行一些优化，还可以通过缓存的角度来思考，这里就不进行进一步分析和优化啦。

如果你有什么好的建议点可以写在评论区里面，期待你的评论o！

总结

仔细想想，解决这个问题，我们做了哪些事

• 分析问题
• 设计解决方案
• 利用算法知识，生成有效代码逻辑
• 测试
• 优化

github地址