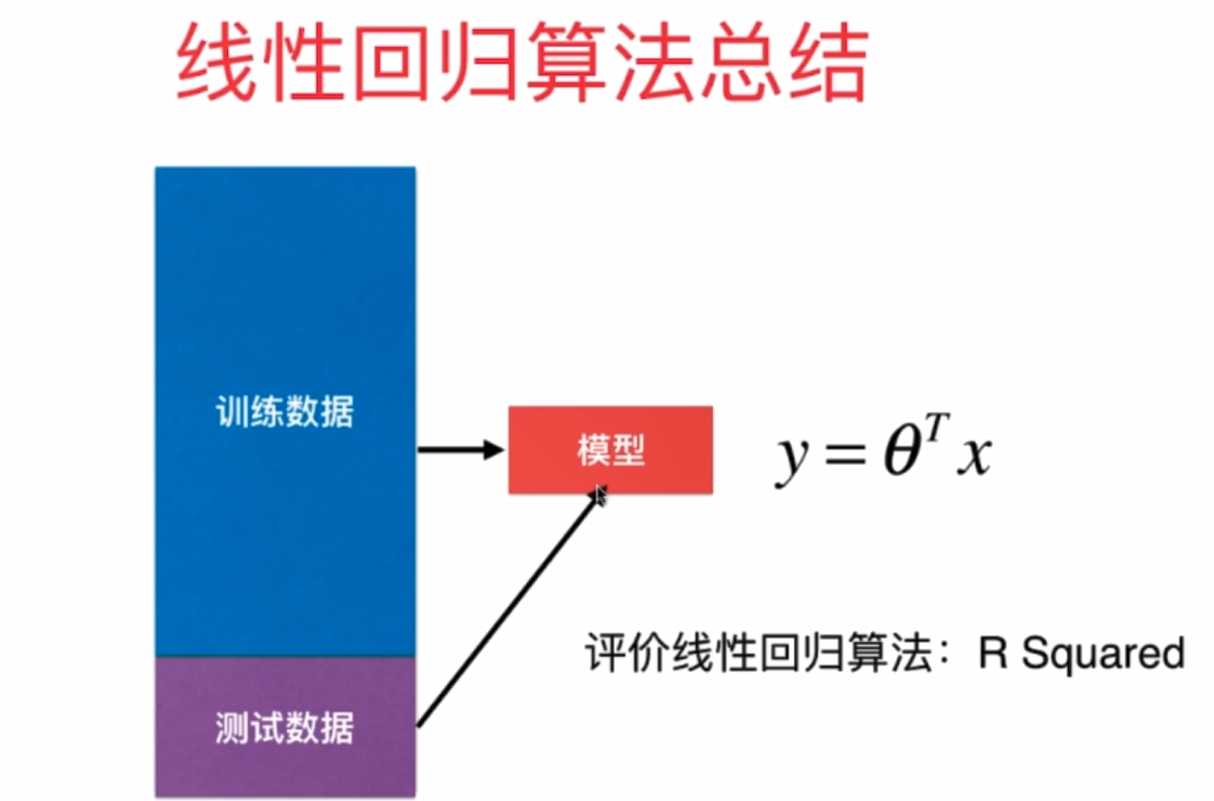
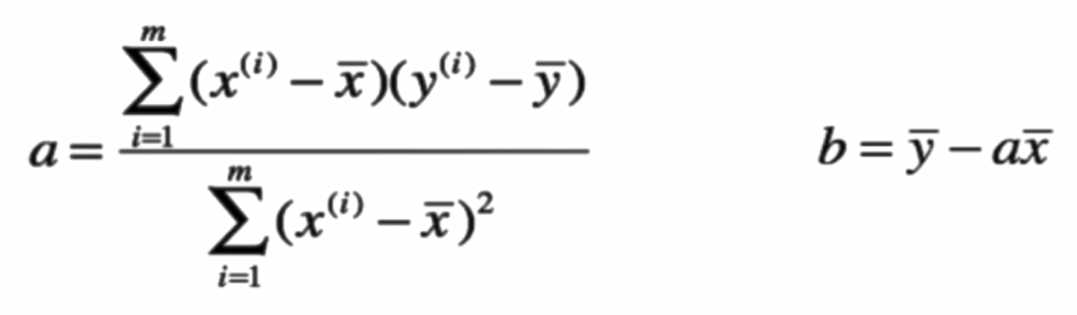1.基本概念

• **线性回归（Linear Regression）**是一种通过属性的线性组合来进行预测的线性模型，其目的是找到一条直线或者一个平面或者更高维的超平面，使得预测值与真实值之间的误差最小化。

2.特点

• 优点：结果具有很好的可解释性（w直观表达了各属性在预测中的重要性），计算熵不复杂。
• 缺点：对非线性数据拟合不好
• 适用数据类型：数值型和标称型数据
  
  
  

3.自己实现的线性回归

3.1 简单线性回归

1.利用最小二乘法得到的系数

2.用简答随机数模拟的方法来搭建简单线性回归

import numpy as np
import matplotlib.pyplot as plt
x = np.array([1., 2., 3., 4., 5.])
y = np.array([1., 3., 2., 3., 5.])

x_mean = np.mean(x)
y_mean = np.mean(y)
num = 0.0
d = 0.0
for x_i, y_i in zip(x, y):
    num += (x_i - x_mean) * (y_i - y_mean)
    d += (x_i - x_mean) ** 2
a = num/d
b = y_mean - a * x_mean
y_hat = a * x + b
x_predict = 6
y_predict = a * x_predict + b

自己封装好的类

import numpy as np


class SimpleLinearRegression1:

    def __init__(self):
        """初始化Simple Linear Regression 模型"""
        self.a_ = None
        self.b_ = None

    def fit(self, x_train, y_train):
        """根据训练数据集x_train,y_train训练Simple Linear Regression模型"""
        assert x_train.ndim == 1, \
            "Simple Linear Regressor can only solve single feature training data."
        assert len(x_train) == len(y_train), \
            "the size of x_train must be equal to the size of y_train"

        x_mean = np.mean(x_train)
        y_mean = np.mean(y_train)

        num = 0.0
        d = 0.0
        for x, y in zip(x_train, y_train):
            num += (x - x_mean) * (y - y_mean)
            d += (x - x_mean) ** 2

        self.a_ = num / d
        self.b_ = y_mean - self.a_ * x_mean

        return self

    def predict(self, x_predict):
        """给定待预测数据集x_predict，返回表示x_predict的结果向量"""
        assert x_predict.ndim == 1, \
            "Simple Linear Regressor can only solve single feature training data."
        assert self.a_ is not None and self.b_ is not None, \
            "must fit before predict!"

        return np.array([self._predict(x) for x in x_predict])

    def _predict(self, x_single):
        """给定单个待预测数据x，返回x的预测结果值"""
        return self.a_ * x_single + self.b_

    def __repr__(self):
        return "SimpleLinearRegression1()"


class SimpleLinearRegression2:

    def __init__(self):
        """初始化Simple Linear Regression模型"""
        self.a_ = None
        self.b_ = None

    def fit(self, x_train, y_train):
        """根据训练数据集x_train,y_train训练Simple Linear Regression模型"""
        assert x_train.ndim == 1, \
            "Simple Linear Regressor can only solve single feature training data."
        assert len(x_train) == len(y_train), \
            "the size of x_train must be equal to the size of y_train"

        x_mean = np.mean(x_train)
        y_mean = np.mean(y_train)

        self.a_ = (x_train - x_mean).dot(y_train - y_mean) / (x_train - x_mean).dot(x_train - x_mean)
        self.b_ = y_mean - self.a_ * x_mean

        return self

    def predict(self, x_predict):
        """给定待预测数据集x_predict，返回表示x_predict的结果向量"""
        assert x_predict.ndim == 1, \
            "Simple Linear Regressor can only solve single feature training data."
        assert self.a_ is not None and self.b_ is not None, \
            "must fit before predict!"

        return np.array([self._predict(x) for x in x_predict])

    def _predict(self, x_single):
        """给定单个待预测数据x_single，返回x_single的预测结果值"""
        return self.a_ * x_single + self.b_

    def __repr__(self):
        return "SimpleLinearRegression2()"

<注> SimpleLinearRegression2（）相比 SimpleLinearRegression1（）是采用向量化的方法实现。采用向量化的方法可以很大程度减少计算机运行时间，提高效率。

3.衡量回归算法的标准
1）相应的公式



2）实现的函数：

import numpy as np
from math import sqrt


def accuracy_score(y_true, y_predict):
    """计算y_true和y_predict之间的准确率"""
    assert len(y_true) == len(y_predict), \
        "the size of y_true must be equal to the size of y_predict"

    return np.sum(y_true == y_predict) / len(y_true)


def mean_squared_error(y_true, y_predict):
    """计算y_true和y_predict之间的MSE"""
    assert len(y_true) == len(y_predict), \
        "the size of y_true must be equal to the size of y_predict"

    return np.sum((y_true - y_predict)**2) / len(y_true)


def root_mean_squared_error(y_true, y_predict):
    """计算y_true和y_predict之间的RMSE"""

    return sqrt(mean_squared_error(y_true, y_predict))


def mean_absolute_error(y_true, y_predict):
    """计算y_true和y_predict之间的MAE"""

    return np.sum(np.absolute(y_true - y_predict)) / len(y_true)

4. R square大小衡量算法的好坏 （也是衡量不同算法的重要标准，使其值在0-1之间，值越大，算法准确度越高）
   1）具体公式
   
   

def r2_score(y_true, y_predict):
    """计算y_true和y_predict之间的R Square"""

    return 1 - mean_squared_error(y_true, y_predict)/np.var(y_true)

5.多元线性回归实现
1）多元线性回归的正规方程解

其中Xb是在X或X_train上添加一列值为一的向量构成的矩阵。目的是个theta匹配。包含θ0这一项。
2）手写封装该算法的类

import numpy as np
from .metrics import r2_score


class LinearRegression:

    def __init__(self):
        """初始化Linear Regression模型"""
        self.coef_ = None
        self.intercept_ = None
        self._theta = None

    def fit_normal(self, X_train, y_train):
        """根据训练数据集X_train, y_train训练Linear Regression模型"""
        assert X_train.shape[0] == y_train.shape[0], \
            "the size of X_train must be equal to the size of y_train"

        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
        self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)

        self.intercept_ = self._theta[0]
        self.coef_ = self._theta[1:]

        return self

    def predict(self, X_predict):
        """给定待预测数据集X_predict，返回表示X_predict的结果向量"""
        assert self.intercept_ is not None and self.coef_ is not None, \
            "must fit before predict!"
        assert X_predict.shape[1] == len(self.coef_), \
            "the feature number of X_predict must be equal to X_train"

        X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
        return X_b.dot(self._theta)

    def score(self, X_test, y_test):
        """根据测试数据集 X_test 和 y_test 确定当前模型的准确度"""

        y_predict = self.predict(X_test)
        return r2_score(y_test, y_predict)

    def __repr__(self):
        return "LinearRegression()"

coef_项是对应θ的系数，intercept_是对应θ0截距项。

4.scikit-learn中的线性回归

from sklearn.linear_model import LinearRegression

lin_reg = LinearRegression()
lin_reg.fit(X_train, y_train)
lin_reg.coef_
lin_reg.intercept_
lin_reg.score(X_test, y_test)

<注》此算法不用提前对数据进行归一化

5.补充利用KNN以及网格搜索法实现回归算法

from sklearn.preprocessing import StandardScaler

standardScaler = StandardScaler()
standardScaler.fit(X_train, y_train)
X_train_standard = standardScaler.transform(X_train)
X_test_standard = standardScaler.transform(X_test)
from sklearn.neighbors import KNeighborsRegressor

knn_reg = KNeighborsRegressor()
knn_reg.fit(X_train_standard, y_train)
knn_reg.score(X_test_standard, y_test)
from sklearn.model_selection import GridSearchCV

param_grid = [
    { 
   
        "weights": ["uniform"],
        "n_neighbors": [i for i in range(1, 11)]
    },
    { 
   
        "weights": ["distance"],
        "n_neighbors": [i for i in range(1, 11)],
        "p": [i for i in range(1,6)]
    }
]

knn_reg = KNeighborsRegressor()
grid_search = GridSearchCV(knn_reg, param_grid, n_jobs=-1, verbose=1)
grid_search.fit(X_train_standard, y_train)
grid_search.best_params_
grid_search.best_score_
grid_search.best_estimator_.score(X_test_standard, y_test)
grid_search.best_estimator_.score(X_test_standard, y_test)

6.思考

在绝大多数情况，在未知数据分布的时，对数据进行分类，预测。首先做的应该数据的预处理。之后，对于模型的搭建，不知其满足的分布时，首先用线性回归方法进行预测，应该是第一步。因为其简单，直观，然后再用其他算法更正。

今天的文章机器学习之线性回归算法分享到此就结束了，感谢您的阅读。