1. 编程号首页

NOIP 2010 普及组初赛试题——答案及解析、错题分析

编程小号 • • 未分类

NOIP 2010 普及组初赛试题——答案及解析、错题分析NOIP2010普及组初赛试题-洛谷有题第1题浮点数2E+03表示（）。A.2.03B.5C.8D.2000第2题一个字节（byte）由（）个二进制位组成。A.8B.16C.32D.以上都有可能第3题以下逻辑表达式的值恒为真的是（）。A.P∨(¬P∧Q)∨(¬P∧¬Q)B.Q∨(¬P∧Q)∨(P∧¬Q)C.P∨Q∨(P∧¬Q)∨(¬P∧Q)D.P∨¬Q∨(P∧¬Q)∨(¬P∧¬Q)第4题Linux下可执行文件的默认扩展

NOIP 2010 普及组初赛试题-洛谷有题

第 1 题
浮点数2E+03表示（ ）。
A. 2.03
B. 5
C. 8
D. 2000
第 2 题
一个字节（byte）由（ ）个二进制位组成。
A. 8
B. 16
C. 32
D. 以上都有可能
第 3 题
以下逻辑表达式的值恒为真的是（ ）。
A. P∨(¬P∧Q)∨(¬P∧¬Q)
B. Q∨(¬P∧Q)∨(P∧¬Q)
C. P∨Q∨(P∧¬Q)∨(¬P∧Q)
D. P∨¬Q∨(P∧¬Q)∨(¬P∧¬Q)
第 4 题
Linux下可执行文件的默认扩展名为（ ）。
A. exe
B. com
C. dll
D. 以上都不是

第 5 题
如果树根算第1层，那么一棵n层的二叉树最多有（ ）个结点。
A. 2n-1
B. 2n
C. 2n+1
D. 2n+1

第 6 题
提出“存储程序”的计算机工作原理的是（ ）。
A. 克劳德·香农
B. 戈登·摩尔
C. 查尔斯·巴比奇
D. 冯·诺依曼

第 7 题
设X、Y、Z分别代表三进制下的一位数字，若等式XY + ZX = XYX在三进制下成立，那么同样在三进制下，等式XY * ZX = （ ）也成立。
A. YXZ
B. ZXY
C. XYZ
D. XZY

第 8 题
Pascal语言、C语言和C++语言都属于（ ）。
A. 面向对象语言
B. 脚本语言
C. 解释性语言
D. 编译性语言

第 9 题
前缀表达式·+ 3 * 2 + 5 12·的值是（ ）。
A. 23
B. 25
C. 37
D. 65

第 10 题
主存储器的存取速度比中央处理器（CPU）的工作速度慢得多，从而使得后者的效率受到影响。而根据局部性原理，CPU所访问的存储单元通常都趋于聚集在一个较小的连续区域中。于是，为了提高系统整体的执行效率，在CPU中引入了（ ）。
A. 寄存器
B. 高速缓存
C. 闪存
D. 外存

第 11 题
一个字长为8位的整数的补码是11111001，则它的原码是（ ）。
A. 00000111
B. 01111001
C. 11111001
D. 10000111

第 12 题
基于比较的排序时间复杂度的下限是（ ），其中n表示待排序的元素个数。
A. Θ(n)
B. Θ(n log n)
C. Θ(log n)
D. Θ(n^2)

第 13 题
一个自然数在十进制下有n位，则它在二进制下的位数与（ ）最接近。
在这里插入图片描述

第 14 题
在下列HTML语句中，可以正确产生一个指向NOI官方网站的超链接的是（ ）。
A. <a url="http://www.noi.cn">欢迎访问NOI网站</a>
B. <a href="http://www.noi.cn">欢迎访问NOI网站</a>
C. <a>http://www.noi.cn</a>
D. <a name="http://www.noi.cn">欢迎访问NOI网站</a>

第 15 题
元素R1、R2、R3、R4、R5入栈的顺序为R1、R2、R3、R4、R5。如果第1个出栈的是R3，那么第5个出栈的不可能是（ ）。
A. R1
B. R2
C. R4
D. R5

第 16 题
双向链表中有两个指针域llink和rlink，分别指向该结点的前驱及后继。设p指向链表中的一个结点，它的左右结点均非空。现要求删除结点p，则下面语句序列中错误的是（ ）。
在这里插入图片描述

第 17 题
一棵二叉树的前序遍历序列是ABCDEFG，后序遍历序列是CBFEGDA，则根结点的左子树的结点个数可能是（ ）。
A. 2
B. 3
C. 4
D. 5

第 18 题
关于拓扑排序，下面说法正确的是（ ）。
A. 所有连通的有向图都可以实现拓扑排序
B. 对同一个图而言，拓扑排序的结果是唯一的
C. 拓扑排序中入度为0的结点总会排在入度大于0的结点的前面
D. 拓扑排序结果序列中的第一个结点一定是入度为0的点

第 19 题
完全二叉树的顺序存储方案，是指将完全二叉树的结点从上至下、从左至右依次存放到一个顺序结构的数组中。假定根结点存放在数组的1号位置，则第k号结点的父结点如果存在的话，应当存放在数组的（ ）号位置。
A. 2k
B. 2k+1
C. k/2下取整
D. (k+1)/2下取整

第 20 题
全国青少年信息学奥林匹克系列活动的主办单位是（ ）。
A. 教育部
B. 科技部
C. 共青团中央
D. 中国计算机学会

问题求解

第 21 题
LZW编码是一种自适应词典编码。在编码的过程中，开始时只有一部基础构造元素的编码词典，如果在编码的过程中遇到一个新的词条，则该词条及一个新的编码会被追加到词典中，并用于后继信息的编码。
举例说明，考虑一个待编码的信息串：“xyx yy yy xyx”。初始词典只有3个条目，第一个为x，编码为1；第二个为y，编码为2；第三个为空格，编码为3；于是串”xyx”的编码为1-2-1（其中-为编码分隔符），加上后面的一个空格就是1-2-1-3。但由于有了一个空格，我们就知道前面的”xyx”是一个单词，而由于该单词没有在词典中，我们就可以自适应的把这个词条添加到词典里，编码为4，然后按照新的词典对后继信息进行编码，以此类推。于是，最后得到编码：1-2-1-3-2-2-3-5-3-4。
现在已知初始词典的3个条目如上述，则信息串”yyxy xx yyxy xyx xx xyx”的编码是_________。
第 22 题
队列快照是指在某一时刻队列中的元素组成的有序序列。例如，当元素1、2、3入队，元素1出队后，此刻的队列快照是”2 3″。当元素2、3也出队后，队列快照是””，即为空。现有3个正整数元素依次入队、出队。已知它们的和为8，则共有_________种可能的不同的队列快照（不同队列的相同快照只计一次）。例如，“5 1”、“4 2 2”、””都是可能的队列快照；而”7″不是可能的队列快照，因为剩下的2个正整数的和不可能是1。

阅读程序写结果

第 23 题

#include <iostream>
using namespace std;

void swap(int & a, int & b)
{ 
   
    int t;
    t = a;
    a = b;
    b = t;
}

int main()
{ 
   
    int a1, a2, a3, x;
        
    cin>>a1>>a2>>a3;
    if (a1 > a2)
        swap(a1, a2);
    if (a2 > a3)
        swap(a2, a3);
    if (a1 > a2)
        swap(a1, a2);
    
    cin>>x;
    if (x < a2)
        if (x < a1)
            cout<<x<<' '<<a1<<' '<<a2<<' '<<a3<<endl;
        else
            cout<<a1<<' '<<x<<' '<<a2<<' '<<a3<<endl;
    else
        if (x < a3)
            cout<<a1<<' '<<a2<<' '<<x<<' '<<a3<<endl;
        else
            cout<<a1<<' '<<a2<<' '<<a3<<' '<<x<<endl;    
    return 0;
}

输入：
91 2 20
77

输出：_____________________________________________

第 24 题

阅读程序写结果：

#include <iostream>
using namespace std;

int rSum(int j)
{ 
   
    int sum = 0;
    while (j != 0) { 
   
        sum = sum * 10 + (j % 10);
        j = j / 10;
    }
    return sum;
}

int main()
{ 
   
    int n, m, i;
        
    cin>>n>>m;
    for (i = n; i < m; i++)
        if (i == rSum(i))
            cout<<i<<' ';
    return 0;
}

输入：
90 120

输出：__________________________

第 25 题

#include <iostream>
#include <string>
using namespace std;

int main()
{ 
   
    string s;
    char m1, m2;
    int i;
    
    getline(cin, s);
    m1 = ' ';
    m2 = ' ';
    for (i = 0; i < s.length(); i++)
        if (s[i] > m1) { 
   
            m2 = m1;
            m1 = s[i];
        }
        else if (s[i] > m2)
            m2 = s[i];
    cout<<int(m1)<<' '<<int(m2)<<endl;
    return 0;
}

输入：Expo 2010 Shanghai China 输出：_________

提示：

字符 空格 ‘0’ ‘A’ ‘a’
ASCII码 32 48 65 97

第 26 题

#include <iostream>
using namespace std;

const int NUM = 5;

int r(int n)
{ 
   
    int i;
    if (n <= NUM)
        return n;
    for (i = 1; i <= NUM; i++)
        if (r(n - i) < 0)
            return i;
    return -1;
}

int main()
{ 
   
    int n;
        
    cin>>n;
    cout<<r(n)<<endl;
    return 0;
}

（1）
输入：7
输出：_________（4分）

（2）
输入：16
输出：_________（4分）

完善程序

第 27 题

完善程序：
（哥德巴赫猜想）哥德巴赫猜想是指，任一大于2的偶数都可写成两个质数之和。迄今为止，这仍然是一个著名的世界难题，被誉为数学王冠上的明珠。试编写程序，验证任一大于2且不超过n的偶数都能写成两个质数之和。

#include <iostream>
using namespace std;

int main()
{ 
   
    const int SIZE = 1000;
        
    int n, r, p[SIZE], i, j, k, ans;
    bool tmp;
    
    cin>>n;
    r = 1;
    p[1] = 2;
    for (i = 3; i <= n; i++) { 
   
        [    ①    ];
        for (j = 1; j <= r; j++)
            if (i % [     ②   ]  == 0) { 
   
                tmp = false;
                break;
            }
        if (tmp) { 
   
            r++;
            [    ③   ] ;
        }
    }
    
    ans = 0;
    for (i = 2; i <= n / 2; i++) { 
   
        tmp = false;
        for (j = 1; j <= r; j++)
            for (k = j; k <= r; k++)
                if (i + i == [     ④   ] ) { 
   
                    tmp = true;
                    break;
                }
        if (tmp)
            ans++;
    }
    cout<<ans<<endl;
    return 0;
}

若输入n为2010，则输出[ ⑤ ]时表示验证成功，即大于2且不超过2010的偶数都满足哥德巴赫猜想。

  1. _________________________________________________

  2. _________________________________________________

  3. _________________________________________________

  4. _________________________________________________

  5. _________________________________________________

第 28 题
**(过河问题）**在一个月黑风高的夜晚，有一群人在河的右岸，想通过唯一的一根独木桥走到河的左岸。在这伸手不见五指的黑夜里，过桥时必须借助灯光来照明，很不幸的是，他们只有一盏灯。另外，独木桥上最多承受两个人同时经过，否则将会坍塌。每个人单独过桥都需要一定的时间，不同的人需要的时间可能不同。两个人一起过桥时，由于只有一盏灯，所以需要的时间是较慢的那个人单独过桥时所花的时间。现输入n（2≤n<100）和这n个人单独过桥时需要的时间，请计算总共最少需要多少时间，他们才能全部到达河的左岸。 例如，有3个人甲、乙、丙，他们单独过桥的时间分别为1、2、4，则总共最少需要的时间为7。具体方法是：甲、乙一起过桥到河的左岸，甲单独回到河的右岸将灯带回，然后甲、丙再一起过桥到河的左岸，总时间为2+1+4=7。

#include <iostream>
using namespace std;

const int SIZE = 100;
const int INFINITY = 10000;
const bool LEFT = true;
const bool RIGHT = false;
const bool LEFT_TO_RIGHT = true;
const bool RIGHT_TO_LEFT = false;

int n, hour[SIZE];
bool pos[SIZE];

int max(int a, int b)
{ 
   
    if (a > b)
        return a;
    else
        return b;
}

int go(bool stage)
{ 
   
    int i, j, num, tmp, ans;
    if (stage == RIGHT_TO_LEFT) { 
   
        num = 0;
        ans = 0;
        for (i = 1; i <= n; i++)
            if (pos[i] == RIGHT) { 
   
                num++;
                if (hour[i] > ans)
                    ans = hour[i];
            }
        if ([    ①    ])
            return ans;
        ans = INFINITY;
        for (i = 1; i <= n - 1; i++)
            if (pos[i] == RIGHT)
                for (j = i + 1; j <= n; j++)
                    if (pos[j] == RIGHT) { 
   
                        pos[i] = LEFT;
                        pos[j] = LEFT;
                        tmp = max(hour[i], hour[j]) +[     ②    ];
                        if (tmp < ans)
                           ans = tmp;
                        pos[i] = RIGHT;
                        pos[j] = RIGHT;
                    }
        return ans;
    }
    if (stage == LEFT_TO_RIGHT) { 
   
        ans = INFINITY;
        for (i = 1; i <= n; i++)
            if ([    ③    ]) { 
   
                pos[i] = RIGHT;
                tmp =[    ④    ];
                if (tmp < ans)
                    ans = tmp;
            [        ⑤    ];
            }
        return ans;
    }
    return 0;
}

int main()
{ 
   
    int i;
        
    cin>>n;
    for (i = 1; i <=n; i++) { 
   
        cin>>hour[i];
        pos[i] = RIGHT;
    }
    cout<<go(RIGHT_TO_LEFT)<<endl;
    return 0;
}

  1. _________________________________________________

  2. _________________________________________________

  3. _________________________________________________

  4. _________________________________________________

  5. _________________________________________________

答案以及解析

在这里插入图片描述

可以来这里查看解析https://www.longkui.site/noip/noip2010pans/535/

选择题错题记录

我得了82.5分，是通过了，心情还不错。

2021年4月5日总结

选择题4：注意linux的可执行文件是没有扩展名的

选择题16：{

A中将p的后继的前驱改为指向p的后继，p的前驱的后继改为指向p的前驱，这样链表就断了
}

选择题18：{

A：当图中有环时必然无法实现拓扑排序；

B：同一时刻，入度为0的点不唯一，拓扑排序也就不唯一；

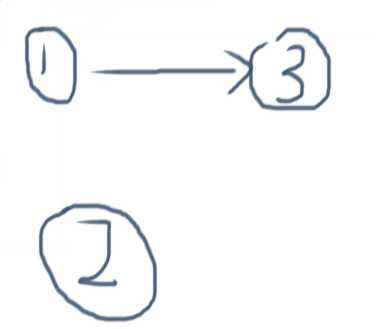
C：如下也是正确的拓扑排序，但是3却在2之前

在这里插入图片描述

}

今天的文章NOIP 2010 普及组初赛试题——答案及解析、错题分析分享到此就结束了，感谢您的阅读。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请发送邮件至 举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/24032.html

赞 (0)
编程小号编程小号
0

相关推荐

发表回复

您的电子邮箱地址不会被公开。 必填项已用*标注