概念
互信息,Mutual Information,缩写为MI,表示两个变量X与Y是否有关系,以及关系的强弱。
公式
我们定义互信息的公式为:
I(X,Y)=∫X∫YP(X,Y)logP(X,Y)P(X)P(Y)
可以看出,如果X与Y独立,则P(X,Y)=P(X)P(Y),I(X,Y)就为0,即代表X与Y不相关
解析公式
其中,H(Y)是Y的熵,定义为
H(Y)=−∫YP(Y)logP(Y)
Y的熵指的是衡量的是Y的不确定度,Y分布得越离散,H(Y)的值越高
H(Y|X)则表示在已知X的情况下,Y的不确定度
所以,根据互信息公式的变形:
I(X,Y)=H(Y)−H(Y|X)
可以看出,I(X,Y)可以解释为由X引入而使Y的不确定度减小的量,这个减小的量为H(Y|X)
所以,如果X,Y关系越密切,I(X,Y)就越大
I(X,Y)最大的取值是H(Y)H(Y),此时H(Y|X)为0,意义为X和Y完全相关,在X确定的情况下Y是个定值,没有出现其他不确定情况的概率,所以为H(Y|X)为0
I(X,Y)取0时,代表X与Y独立,此时H(Y)=H(Y|X),意义为X的出现不影响Y。。
性质
I(X;Y)I(X;Y)的性质:
1)I(X;Y)⩾0 ,I(X;Y)⩾0
2)H(X)−H(X|Y)=I(X;Y)=I(Y;X)=H(Y)−H(Y|X)H(X)−H(X|Y)=I(X;Y)=I(Y;X)=H(Y)−H(Y|X)
3)当X,Y独立时,I(X;Y)=0,I(X;Y)=0
4)当X,Y知道一个就能推断另一个时,I(X;Y)=H(X)=H(Y)
缺点
在做文本分类时,我们可能会判断一个词和某类的相关程度,但是计算时,未考虑词频的影响
(可以让互信息的结果再乘上tf-idf因子,从而将特征频率与特征分布考虑进去)
应用
1、文本自动摘要
2、两个词语同时出现的概率
PMI(点互信息),通过判断一个词分别与poor和excellent的互信息来判断这个词的情感倾向
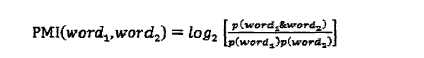
3、特征提取时特征项与类别的关联程度
更多
http://www.docin.com/p-1061736680.html 一个互信息的文本摘要应用
http://www.cnblogs.com/ywl925/p/3736277.html
参考文献:
http://www.fuzihao.org/blog/2015/01/17/%E4%BA%92%E4%BF%A1%E6%81%AF%E7%9A%84%E7%90%86%E8%A7%A3/
后续遇到应用再补充MI的更多用途
今天的文章互信息(Mutual Information)的介绍分享到此就结束了,感谢您的阅读,如果确实帮到您,您可以动动手指转发给其他人。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/24520.html

