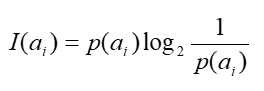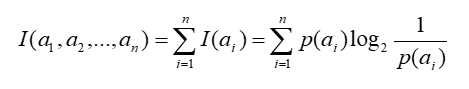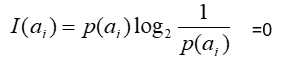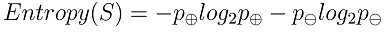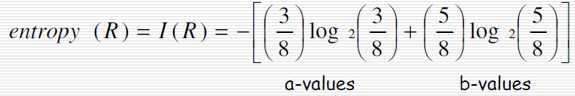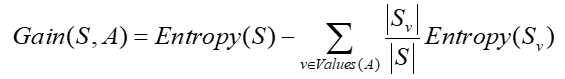R语言学习(三)——决策树分类

分类

分类（Classification）任务就是通过学习获得一个目标函数（Target Function）f, 将每个属性集x映射到一个预先定义好的类标号y。

分类任务的输入数据是记录的集合，每条记录也称为实例或者样例。用元组(X,y)表示，其中，X 是属性集合，y是一个特殊的属性，指出样例的类标号（也称为分类属性或者目标属性）。

解决分类问题的一般方法

分类技术是一种根据输入数据集建立分类模型的系统方法。

分类技术一般是用一种学习算法确定分类模型，该模型可以很好地拟合输入数据中类标号和属性集之间的联系。学习算法得到的模型不仅要很好拟合输入数据，还要能够正确地预测未知样本的类标号。因此，训练算法的主要目标就是要建立具有很好的泛化能力模型，即建立能够准确地预测未知样本类标号的模型。

分类方法的实例包括：决策树分类法、基于规则的分类法、神经网络、支持向量机、朴素贝叶斯分类方法等。

通过以上对分类问题一般方法的描述，可以看出分类问题一般包括两个步骤：

1. 模型构建（归纳）
   通过对训练集合的归纳，建立分类模型。

2. 预测应用（推论）
   根据建立的分类模型，对测试集合进行测试。

决策树

决策树是一种典型的分类方法，首先对数据进行处理，利用归纳算法生成可读的规则和决策树，然后使用决策对新数据进行分析。本质上决策树是通过一系列规则对数据进行分类的过程。

决策树的优点

1. 推理过程容易理解，决策推理过程可以表示成If Then形式；
2. 推理过程完全依赖于属性变量的取值特点；
3. 可自动忽略目标变量没有贡献的属性变量，也为判断属性变量的重要性，减少变量的数目提供参考。

决策树算法

与决策树相关的重要算法：CLS, ID3，C4.5，CART

1. Hunt,Marin和Stone 于1966年研制的CLS学习系统，用于学习单个概念。
2. 1979年, J.R. Quinlan 给出ID3算法，并在1983年和1986年对ID3
   进行了总结和简化，使其成为决策树学习算法的典型。
3. Schlimmer和Fisher于1986年对ID3进行改造，在每个可能的决策树节点创建缓冲区，使决策树可以递增式生成，得到ID4算法。
4. 1988年，Utgoff 在ID4基础上提出了ID5学习算法，进一步提高了效率。 1993年，Quinlan
   进一步发展了ID3算法，改进成C4.5算法。
5. 另一类决策树算法为CART，与C4.5不同的是，CART的决策树由二元逻辑问题生成，每个树节点只有两个分枝，分别包括学习实例的正例与反例。

决策树的表示

决策树的基本组成部分：决策结点、分支和叶子。

决策树中最上面的结点称为根结点，是整个决策树的开始。每个分支是一个新的决策结点，或者是树的叶子。每个决策结点代表一个问题或者决策.通常对应待分类对象的属性。每个叶结点代表一种可能的分类结果。

在沿着决策树从上到下的遍历过程中，在每个结点都有一个测试。对每个结点上问题的不同测试输出导致不同的分枝，最后会达到一个叶子结点。这一过程就是利用决策树进行分类的过程，利用若干个变量来判断属性的类别。

ID3

ID3算法主要针对属性选择问题。是决策树学习方法中最具影响和最为典型的算法。

该方法使用信息增益度选择测试属性。

• 信息量大小的度量

Shannon1948年提出的信息论理论。事件ai的信息量I(ai )可如下度量：

其中p(ai)表示事件ai发生的概率。

假设有n个互不相容的事件a1,a2,a3,….,an,它们中有且仅有一个发生，则其平均的信息量可如下度量：

由上式，对数底数可以为任何数，不同的取值对应了熵的不同单位。

通常取2，并规定当p(ai)=0时：

• 熵

用熵度量样例的均一性

熵刻画了任意样例集合 S 的纯度

给定包含关于某个目标概念的正反样例的样例集S，那么 S 相对这个布尔型分类（函数）的熵为：

信息论中对熵的一种解释：熵确定了要编码集合S中任意成员的分类所需要的最少二进制位数；熵值越大，需要的位数越多。

更一般地，如果目标属性具有c个不同的值，那么 S 相对于c个状态的分类的熵定义为：

例如：求集合R = {a,a,a,b,b,b,b,b}的信息熵

理解信息熵：

1. 信息熵是用来衡量一个随机变量出现的期望值，一个变量的信息熵越大，那么它出现的各种情况也就越多，也就是包含的内容多，我们要描述它就需要付出更多的表达才可以，也就是需要更多的信息才能确定这个变量。
2. 信息熵是随机变量的期望。度量信息的不确定程度。信息的熵越大，信息就越不容易搞清楚（杂乱）。
3. 一个系统越是有序，信息熵就越低；反之，一个系统越是混乱，信息熵就越高。信息熵也可以说是系统有序化程度的一个度量。
4. 信息熵用以表示一个事物的非确定性，如果该事物的非确定性越高，你的好奇心越重，该事物的信息熵就越高。
5. 熵是整个系统的平均消息量。 信息熵是信息论中用于度量信息量的一个概念。一个系统越是有序，信息熵就越低；反之，一个系统越是混乱，信息熵就越高。
6. 处理信息就是为了把信息搞清楚，实质上就是要想办法让信息熵变小。

• 信息增益

用来衡量给定的属性区分训练样例的能力

ID3算法在生成 树的每一步使用信息增益从候选属性中选择属性

用信息增益度量熵的降低程度

属性A 的信息增益，使用属性A分割样例集合S 而导致的熵的降低程度

Gain (S, A)是在知道属性A的值后可以节省的二进制位数

信息增益代表了在一个条件下，信息复杂度（不确定性）减少的程度。

理解信息增益：

熵：表示随机变量的不确定性。
条件熵：在一个条件下，随机变量的不确定性。
信息增益：熵 – 条件熵。表示在一个条件下，信息不确定性减少的程度。
例如：
假设X(明天下雨)的信息熵为2（不确定明天是否下雨），Y(如果是阴天则下雨）的条件熵为0.01（因为如果是阴天就下雨的概率很大，信息就少了） 信息增益=2-0.01=1.99。信息增益很大。说明在获得阴天这个信息后，明天是否下雨的信息不确定性减少了1.99，所以信息增益大。也就是说阴天这个信息对下雨来说是很重要的。

ID3 决策树建立算法

1. 决定分类属性
2. 对目前的数据表，建立一个节点N
3. 如果数据库中的数据都属于同一个类，N就是树叶，在树叶上标出所属的类
4. 如果数据表中没有其他属性可以考虑，则N也是树叶，按照少数服从多数的原则在树叶上标出所属类别
5. 否则，根据平均信息期望值E或GAIN值选出一个最佳属性作为节点N的测试属性
6. 节点属性选定后，对于该属性中的每个值：
   从N生成一个分支，并将数据表中与该分支有关的数据收集形成分支节点的数据表，在表中删除节点属性那一栏如果分支数据表非空，则运用以上算法从该节点建立子树。

小结
ID3算法是一种经典的决策树学习算法，由Quinlan于1979年提出。ID3算法的基本思想是，以信息熵为度量，用于决策树节点的属性选择，每次优先选取信息量最多的属性，亦即能使熵值变为最小的属性，以构造一颗熵值下降最快的决策树，到叶子节点处的熵值为0。此时，每个叶子节点对应的实例集中的实例属于同一类。

R语言中的决策树实现

• 安装数据包

安装rpart、rpart.plot、rattle三个数据包
rpart:用于分类与回归分析
rpart.plot：用于绘制数据模型
rattle:提供R语言数据挖掘图形界面
安装语句：

rpart:install.packages("rpart")
rpart:install.packages("rpart.plot")
install.packages("rattle")

• 步骤1：生成训练集和测试集

以iris数据集为例：
训练集：

iris.train=iris[2*(1:75)-1,] 
返回原数据集1、3、5、7、8、......、149奇数行行所有列的数据

测试集：

iris.test= iris[2*(1:75),] 
返回原数据集2、4、6、8、10、......、150偶数行所有列的数据

• 步骤2：生成决策树模型

加载rpart包：

> library("rpart")

> model <- rpart(Species ~ Sepal.Length + Sepal.Width + Petal.Length + Petal.Width, data = iris.train,  method="class")

rpart参数解释：

rpart(formula, data, method, parms, ...)

1. formula是回归方程的形式，y~x1+x2+…，
   iris一共有5个变量，因变量是Species,自变量是其余四个变量，所以formula可以省略为Species~.
2. data是所要学习的数据集
3. method根据因变量的数据类型有如下几种选择：anova（连续型），poisson（计数型），class（离散型），exp（生存型），因为我们的因变量是花的种类，属于离散型，所以method选择class
4. parms可以设置纯度的度量方法，有gini（默认）和information（信息增益）两种。

• 步骤3：绘制决策树

rpart.plot(model)

或

fancyRpartPlot(model)

• 步骤4：对测试集进行预测

iris.rp3=predict(model, iris.test[,-5], type="class") 

iris.test[,-5]的意思是去掉原测试集第5列后的数据

• 步骤5：查看预测结果并对结果进行分析，计算出该决策树的accuracy（分类正确的样本数除以总样本数）

table(iris.test[,5],iris.rp3) 

可得accuracy=（25+24+22）/75=94.67%

• 步骤6：生成规则

asRules(model)

今天的文章R语言学习(三)——决策树分类分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。