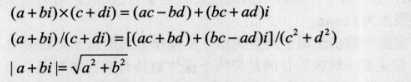目录
一、复数的四则运算
(1)计算方法
-
加法:(a+bi)+(c+di)=(a+c)+(c+d)i【实部与实部相加,虚部与虚步相加】
-
减法:(a+bi)-(c+di)=(a-c)+(c-d)i【实部与实部相减,虚部与虚步相减】
-
乘法:(a+bi)(c+di)=ac+adi+cdi+bdi*i=(ac-bd)+(bc+ad)i【普通的多项式相乘;i^2=-1】
-
除法:(a+bi)/(c+di)=(a+bi)(c-di)/((c+di)(c+di))=((ac+bd)+(bc-ad)i)/(c^2+d^2)【分子分母同时乘以分母的共轭复数,然后上边是乘法,下边也是乘法】
(2)例题:本题要求编写程序,计算2个复数的和、差、积、商。
输入格式:
输入在一行中按照a1 b1 a2 b2的格式给出2个复数C1=a1+b1i和C2=a2+b2i的实部和虚部。题目保证C2不为0。
输出格式:
分别在4行中按照(a1+b1i) 运算符 (a2+b2i) = 结果的格式顺序输出2个复数的和、差、积、商,数字精确到小数点后1位。如果结果的实部或者虚部为0,则不输出。如果结果为0,则输出0.0。
输入样例1:
2 3.08 -2.04 5.06
输出样例1:
(2.0+3.1i) + (-2.0+5.1i) = 8.1i (2.0+3.1i) - (-2.0+5.1i) = 4.0-2.0i (2.0+3.1i) * (-2.0+5.1i) = -19.7+3.8i (2.0+3.1i) / (-2.0+5.1i) = 0.4-0.6i
输入样例2:
1 1 -1 -1.01
输出样例2:
(1.0+1.0i) + (-1.0-1.0i) = 0.0 (1.0+1.0i) - (-1.0-1.0i) = 2.0+2.0i (1.0+1.0i) * (-1.0-1.0i) = -2.0i (1.0+1.0i) / (-1.0-1.0i) = -1.0
#include<stdio.h>
float a, b, c, d;
void sign(char op);
void operation(float e,float f,char op);
int main(void)
{
scanf("%f%f%f%f", &a, &b, &c, &d);
operation(a+c, b+d, '+');
operation(a-c, b-d, '-');
operation(a*c - b*d, a*d + b*c, '*');
operation((a*c + b*d) / (c*c + d*d), (b*c - a*d) / (c*c + d*d), '/');
return 0;
}
void sign(char op)
{
printf("(%.1f", a);
if(b>=0)
printf("+");
printf("%.1fi) %c (%.1f", b, op, c);
if(d>=0)
printf("+");
printf("%.1fi) = ", d);
}
void operation(float e,float f,char op)
{
sign(op);
if((int)(e*10))
printf("%.1f", e);
if((int)(f*10))
{
if ((f > 0) && (int)(e*10))
printf("+");
printf("%.1fi", f);
}
else if (!(int)(e*10))
printf("0.0");
printf("\n");
}
二、复数的头文件#include <complex.h>
(1)C语言中有三个类型可以存储复数
float_Complex:实部和虚部都为float类型
double_Complex:实部和虚部都为double类型
long double_Complex:实部和虚部都为long类型
例如:double_Complex x;
注:C99对复数的支持,用这种定义方法不需要任何头文件。
(2)加入头文件#include <complex.h>,就可以用complex代替_Complex,这个头文件把虚部定义为'I',所以定义定义这样一个复数可以这样float complex z=a+bI;
(3)宏
| 宏名称 | 值 |
|---|---|
| complex | _Complex |
| _Complex_I | 虚数单位,类型为const float_Complex |
| I | _Complex_I |
这里的I代替Complex_I可以类比bool(#include <stdbool>中的)和Bool一样
复数的赋值方法如:doubel complex dc=2.0+3.5*I;
(4)几个函数
1.double real_part=creal(z);//得到Z的实部
2.double imag_part=cimag(z)//得到Z的虚部
在处理float和long double类型时,用crealf()和creall(),cimagf()和cimagl()。【理解:以double complex为基准】
3.延展:允许复数有乘除绝对值操作,但是必须有CX_LIMITED_RANGE的编译提示
4.复数函数拓展

复数有关函数分类:三角函数、双曲函数、指数函数和对数函数、幂函数和操作函数。
操作函数就比如这样的
(2)例题:求一元二次方程的根
特别注意:一元二次方程的虚根求解办法:把负数变成正数,但是需要在他后边加上一个i
所以,实部=-b/(2a),虚部=sqrt(-dert)/(2a)。
描述
从键盘输入a, b, c的值,编程计算并输出一元二次方程ax2 + bx + c = 0的根,当a = 0时,输出“Not quadratic equation”,当a ≠ 0时,根据△ = b2 – 4ac的三种情况计算并输出方程的根。
输入描述:
多组输入,一行,包含三个浮点数a, b, c,以一个空格分隔,表示一元二次方程ax2 + bx + c = 0的系数。
输出描述:
针对每组输入,输出一行,输出一元二次方程ax2 + bx +c = 0的根的情况。
如果a = 0,输出“Not quadratic equation”;
如果a ≠ 0,分三种情况:
△ = 0,则两个实根相等,输出形式为:x1=x2=…。
△ > 0,则两个实根不等,输出形式为:x1=…;x2=…,其中x1 <= x2。
△ < 0,则有两个虚根,则输出:x1=*实部-虚部i;x2=实部+虚部i**,即x1的虚部系数小于等于x2的虚部系数,实部为0时不可省略。实部= -b / (2a),虚部= sqrt(-△ ) / (2*a)
所有实数部分要求精确到小数点后2位,数字、符号之间没有空格。
示例1
输入:
2.0 7.0 1.0
输出:
x1=-3.35;x2=-0.15
#include <stdio.h>
#include <math.h>
double zhengen(double m, double n, double d);//实现一元二次方程求根公式函数+
double fugen(double m, double n, double d);//实现一元二次方程求根公式函数-
double shibu(double m, double n);
double xubu(double m, double d);
int main()
{
double a = 0, b = 0, c = 0,x1=0,x2=0;
while(scanf("%lf %lf %lf", &a, &b, &c)!=EOF)
{
double derta = pow(b, 2) - 4 * a * c;
if (a != 0)//第一个参数不为0
{
if (derta == 0)//①=0
{
if(b==0)//这个直接丢了也可以,只是会多算一点
printf("x1=x2=0.00\n");
else
{
x1 = x2 = zhengen(a,b,derta);
printf("x1=x2=%.2lf\n", x1);
}
}
else if (derta > 0)//②>0
{//这里是把较大的解赋给正根,较小的解赋给负根
x1 =( zhengen(a, b, derta)> fugen(a, b, derta)) ? fugen(a, b, derta) : zhengen(a, b, derta);
x2 =(zhengen(a, b, derta) > fugen(a, b, derta)) ? zhengen(a, b, derta) : fugen(a, b, derta);
printf("x1=%.2lf;x2=%.2lf\n",x1,x2);
}
else if (derta < 0)//③<0——虚根
{
if(xubu(a,derta)<0)//要注意正负号和加减号的区别
printf("x1=%.2lf%.2lfi;x2=%.2lf+%.2lfi\n",shibu(a, b),xubu(a, derta), shibu(a, b), -xubu(a, derta));
else
printf("x1=%.2lf-%.2lfi;x2=%.2lf+%.2lfi\n",shibu(a, b),xubu(a, derta), shibu(a, b), xubu(a, derta));
}
}
else
{
printf("Not quadratic equation");//不是二次方程
}
}
return 0;
}
double zhengen(double m, double n, double d)//实现一元二次方程求根公式函数+
{
double x = 0;
x = (-n + sqrt(d)) / (2 * m);
return x;
}
double fugen(double m, double n, double d)//实现一元二次方程求根公式函数-
{
double x = 0;
x = (-n - sqrt(d)) / (2 * m);
return x;
}
double shibu(double m, double n)
{
double s = 0;
s = (-n) / (2 * m);
return s;
}
double xubu(double m, double d)
{
double xu = 0;
xu = sqrt(-d) / (2 * m);
return xu;
}
三、一些碎碎念
这次总结是因为之前做到了一元二次方程的这个编程题,对于虚根就不是特别理解,只不过回头一看,原来题目上说了他们的求法,只是自己没有认真看。然后今天在课上做实验题时,发现有那个复数的四则运算,自己本身复数运算就学的不是太好,在加上编程,双层buff,我天,当时就一个头,两个大,但是又联想到之前做的那个虚根的问题,就想着这次自己一定要把它给攻破。不能再像之前一样,总是发现问题,而不去解决问题,只等着别人把东西喂给自己,自己还可能不吃这个知识点。最后一点点看着自己下滑,别人一点点上升,心有不甘,却又无能为力,四处碰壁。
这次自己主动联想,主动总结有关复数的内容就是一个好的开端。加油~好了,废话到此结束,再回顾一下这次主要弄了什么
1.复数的算术运算/四则运算【计算规则以及计算机表示——这里采用的是4个operation函数,参数都是两个数和一个运算符,两个参数分别是自己根据负数的运算规则计算出的实部和虚部;然后一个主要打印等式的函数sign(这里需要特别注意里边符号的打印就比如说实部/虚部的正负==>+/-)】
2.一元二次方程【整体分为2种情况a>0与a<0,其中a>0分为3种情况,一种是dert>0,dert<0,dert=0.然后dert<0的情况需要计算实部(-b/2a)和虚部(sqrt(-dert)/2a);这里的计算很多,我们把它给封装成函数会更加方便——zhengen+fugen+shibu+xubu】
3.对头文件#include <complex.h>有了了解,比如定义3种类型的变量,得到有了一个复数的实部,得到一个复数的虚部。至于其他的都只是拓展阅读吧,没有实例和应用场景,理解会不到位。比如说I、complex等是宏定义来的,还有一些复数的函数(一般都是以c开头的,比如csin)一些了解。
今天的文章【C语言】复数的四则运算与复数运算的头文件分享到此就结束了,感谢您的阅读,如果确实帮到您,您可以动动手指转发给其他人。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/26801.html