Continuous function – FT & Conv
有两个时域函数 g ( t ) g(t) g(t) 和 h ( t ) h(t) h(t), 则有时域卷积等价于频域相乘 (反之亦然, 仅多一个系数), 即
结论:FT ( g ∗ h ) (g\ast h) (g∗h)=FT ( g ) × (g)\times (g)×FT ( h ) (h) (h)
证明:两者卷积后的函数 p ( t ) p(t) p(t) 可写作
p ( t ) = g ( t ) ∗ h ( t ) = ∫ − ∞ ∞ g ( τ ) h ( t − τ ) d τ p(t)=g(t)\ast h(t)=\int_{-\infty}^\infty g(\tau)h(t-\tau)d\tau p(t)=g(t)∗h(t)=∫−∞∞g(τ)h(t−τ)dτ
进一步, p ( t ) p(t) p(t) 的傅里叶变换为
P ( f ) = ∫ − ∞ ∞ p ( t ) e j 2 π f t d t = ∫ − ∞ ∞ ∫ − ∞ ∞ g ( τ ) h ( t − τ ) d τ e − j 2 π f t d t = ∫ − ∞ ∞ h ( t − τ ) e − j 2 π f t d t ∫ − ∞ ∞ g ( τ ) d τ = ∫ − ∞ ∞ h ( t ′ ) e − j 2 π f t ′ d t ′ e − j 2 π f τ ∫ − ∞ ∞ g ( τ ) d τ = H ( f ) ∫ − ∞ ∞ g ( τ ) e − j 2 π f τ d τ = G ( f ) H ( f ) P(f)=\int_{-\infty}^\infty p(t)e^{j2\pi f t}dt=\int_{-\infty}^\infty \int_{-\infty}^\infty g(\tau)h(t-\tau)d\tau e^{-j2\pi f t}dt \\ =\int_{-\infty}^\infty h(t-\tau)e^{-j2\pi f t}dt \int_{-\infty}^\infty g(\tau)d\tau =\int_{-\infty}^\infty h(t')e^{-j2\pi f t'}dt' e^{-j2\pi f \tau}\int_{-\infty}^\infty g(\tau)d\tau\\ =H(f) \int_{-\infty}^\infty g(\tau)e^{-j2\pi f \tau} d\tau= G(f)H(f) P(f)=∫−∞∞p(t)ej2πftdt=∫−∞∞∫−∞∞g(τ)h(t−τ)dτe−j2πftdt=∫−∞∞h(t−τ)e−j2πftdt∫−∞∞g(τ)dτ=∫−∞∞h(t′)e−j2πft′dt′e−j2πfτ∫−∞∞g(τ)dτ=H(f)∫−∞∞g(τ)e−j2πfτdτ=G(f)H(f)
Discrete sequence – DFT & Conv
有两个定义在整数上的函数 g [ n ] g[n] g[n] 和 h [ n ] h[n] h[n], 它们的卷积可以写作
p [ n ] = ∑ i = 0 ∞ g [ i ] h [ n − i ] p[n]=\sum_{i=0}^{\infty}g[i]h[n-i] p[n]=i=0∑∞g[i]h[n−i]
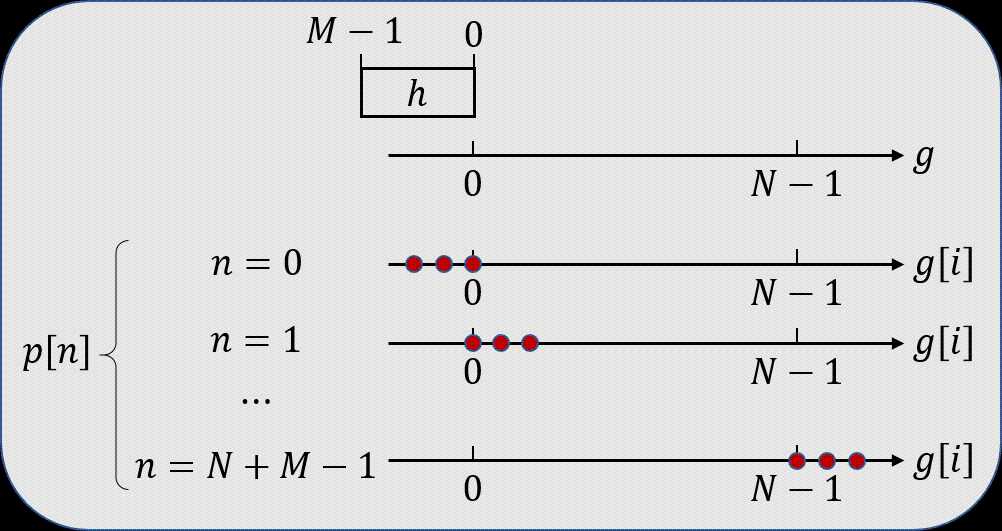
但是当 g [ n ] g[n] g[n] 和 h [ n ] h[n] h[n] 有限长 N N N, M M M时, 他们的卷积可以写作
p [ n ] = ∑ i = 0 N − 1 g [ i ] h [ n − i ] , n = 0 , 1 , 2 , . . . , N + M − 1 p[n]=\sum_{i=0}^{N-1}g[i]h[n-i], n=0,1,2,…,N+M-1 p[n]=i=0∑N−1g[i]h[n−i],n=0,1,2,...,N+M−1
结论:DFT ( g ∗ h ) (g\ast h) (g∗h) = DFT ( g ) × (g)\times (g)×DFT ( h ) (h) (h) 成立当且仅当K点DFT变换的长度 K > N + M − 1 K>N+M-1 K>N+M−1.
这个很显然,因为 g ∗ h g\ast h g∗h 卷积出来的有 N + M − 1 N+M-1 N+M−1 点,DFT点数不能小于这个值。
OFDM symbol – Cyclic Conv
在OFDM信号处理中, g [ n ] g[n] g[n] 一般是对IDFT后一个OFDM符号的 N N N 点采样. h [ n ] h[n] h[n] 一般是多径信道 (其长度 M M M 一般会小于 N N N)。 在接收端,我们的 DFT 只会做 N N N 点的,这就需要 CP 把信道的卷积变成循环卷积。
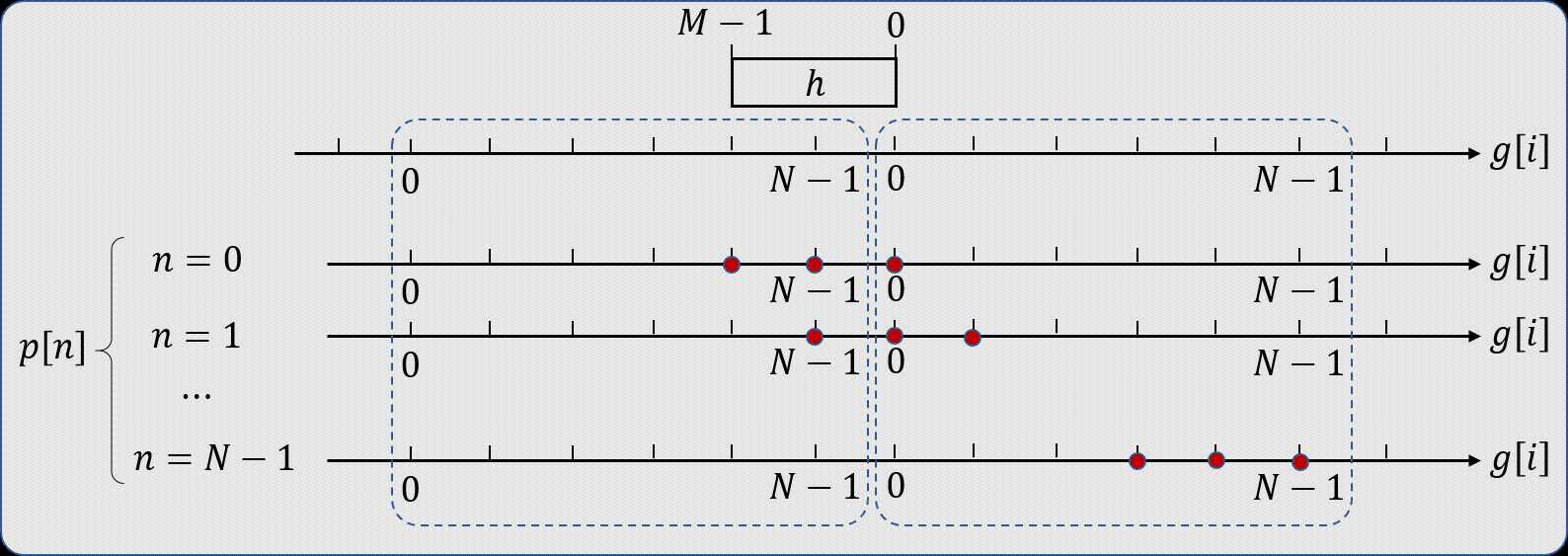
设 g [ n ] g[n] g[n] 和 h [ n ] h[n] h[n] 长度为 N N N, M M M, 且 M ≤ N M\leq N M≤N. 他们的循环卷积可以写作
p [ n ] = g [ n ] ⊗ h [ n ] = ∑ i = 1 − N N − 1 g [ i ] h [ n − i ] , n = 0 , 1 , 2 , . . . , N − 1 p[n]=g[n] \otimes h[n]=\sum_{i=1-N}^{N-1}g[i]h[n-i], n=0,1,2,…,N-1 p[n]=g[n]⊗h[n]=i=1−N∑N−1g[i]h[n−i],n=0,1,2,...,N−1
公式里面的 N N N 其实都应该是 max ( N , M ) \max(N,M) max(N,M),若 M > N M> N M>N 就把 g [ n ] g[n] g[n] 和 h [ n ] h[n] h[n] 倒反就行了。
循环卷积等价于把其中长的那个序列(图中是 g [ n ] g[n] g[n])无限循环延拓,在用另一个短序列滑动相关。这样得出的序列 p [ n ] p[n] p[n] 是一个周期序列,且周期为长序列的长度 (图中是 N N N)。每个 p [ n ] p[n] p[n]都是 min ( N , M ) \min(N,M) min(N,M) 个点相关的结果
今天的文章时域卷积,频域相乘分享到此就结束了,感谢您的阅读,如果确实帮到您,您可以动动手指转发给其他人。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/26863.html