Java的几种经典排序算法

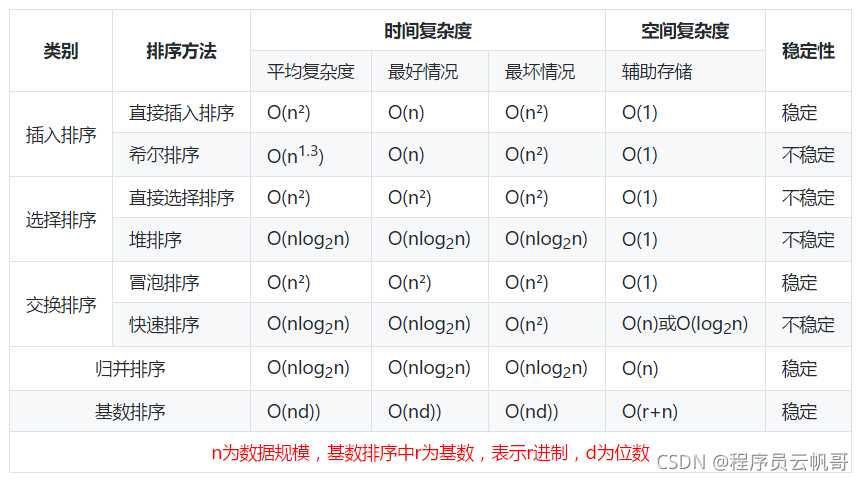
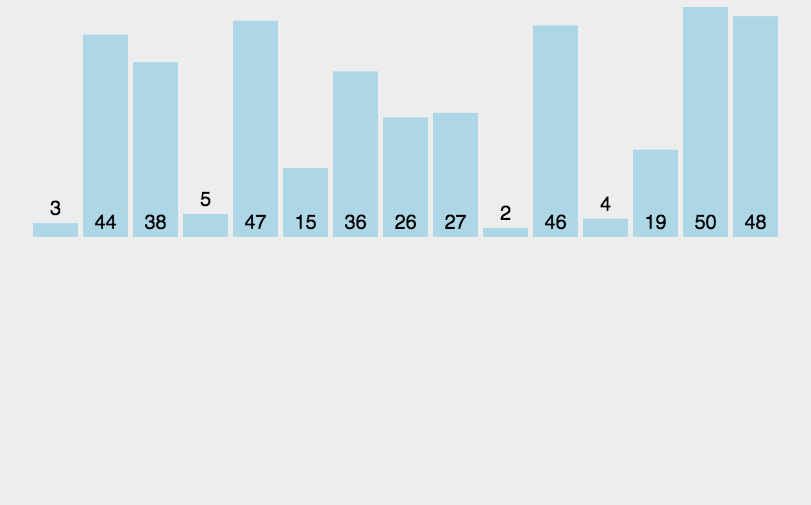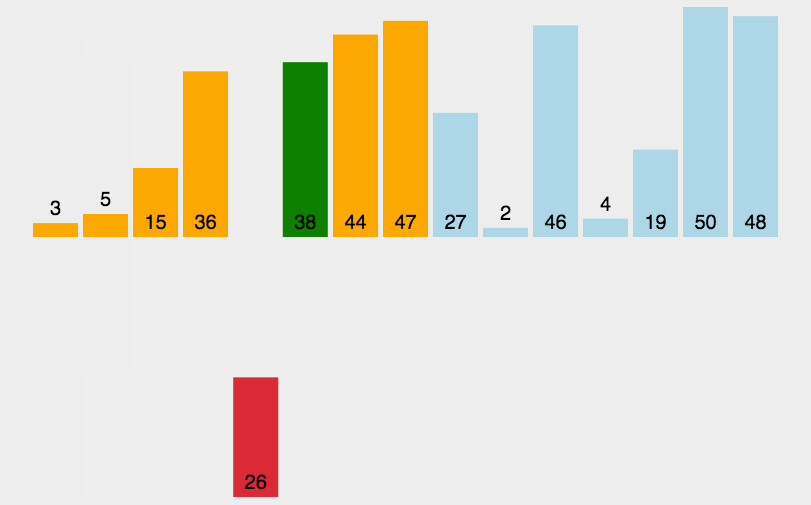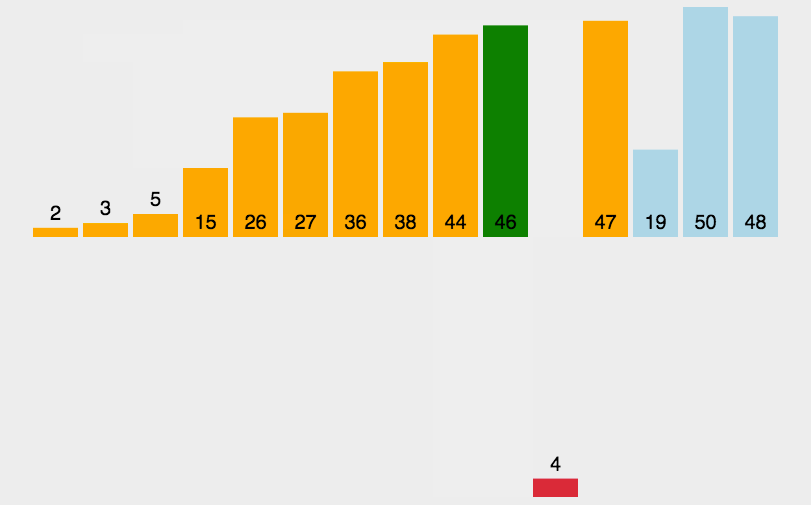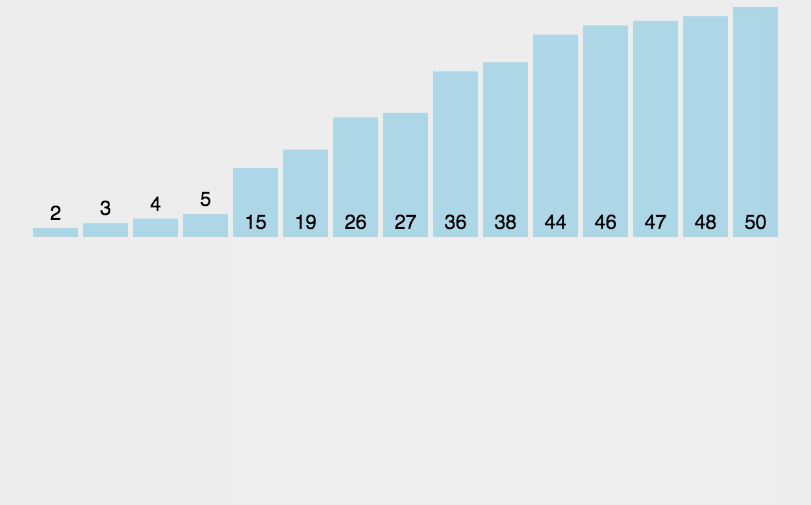
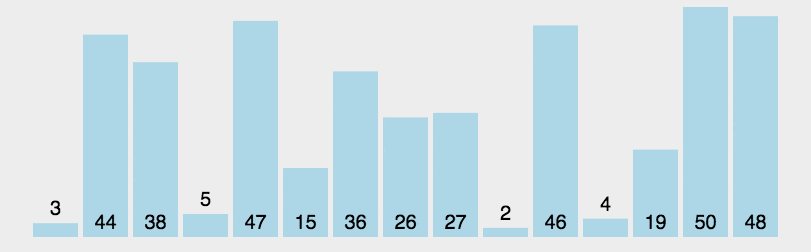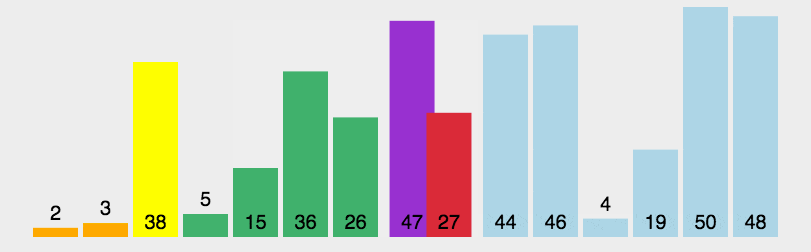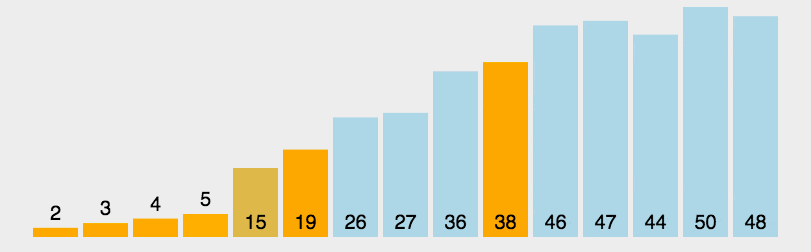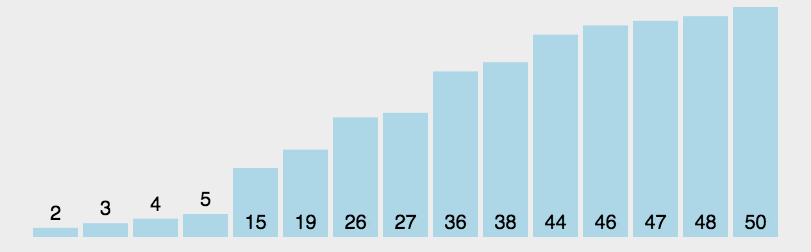
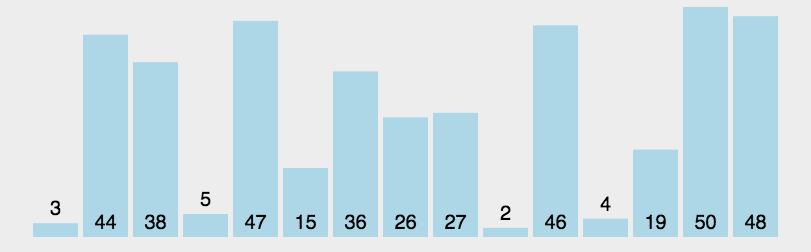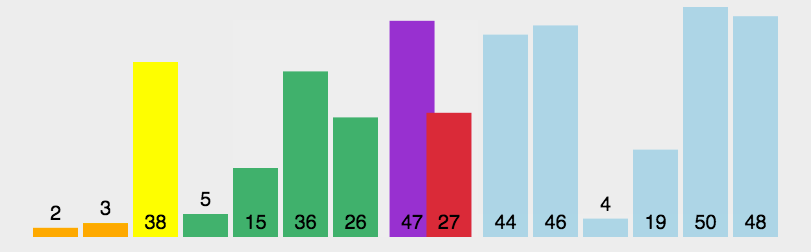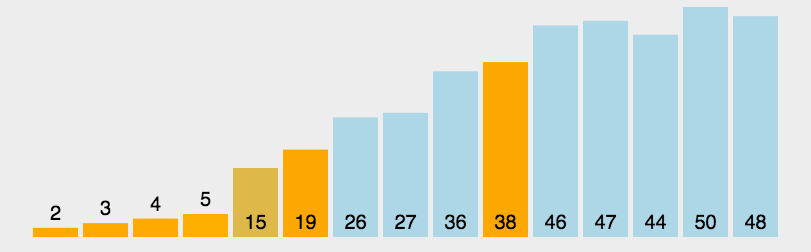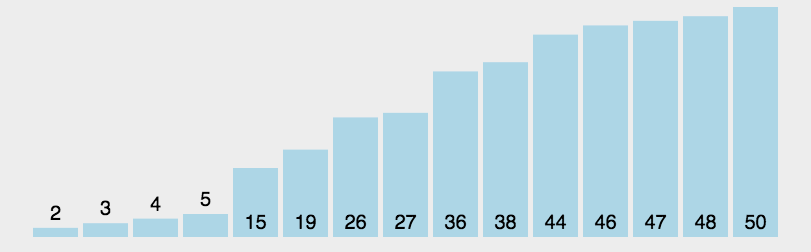
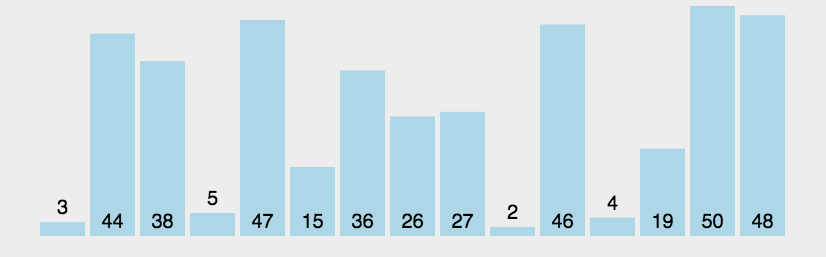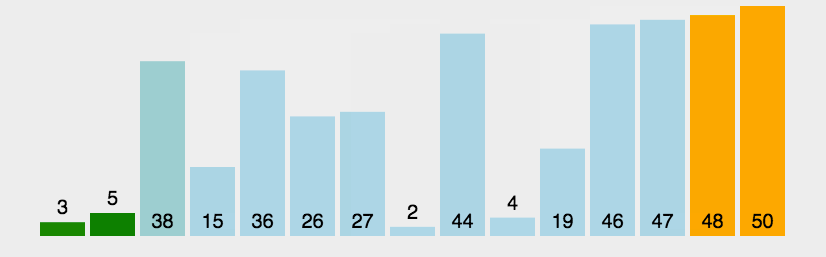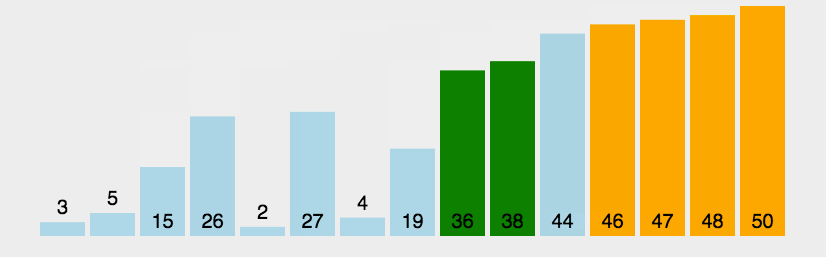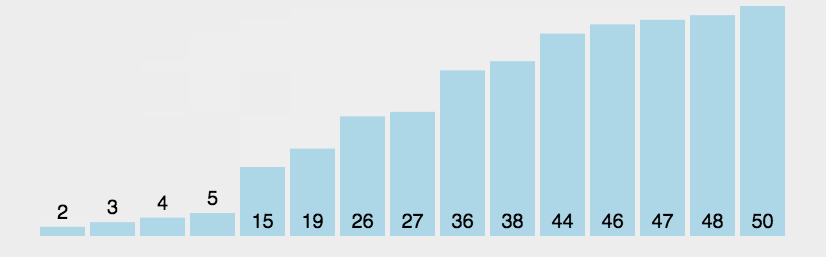对一个排序算法来说，一般从如下3个方面衡量算法的优劣：
时间复杂度：主要是分析关键字的比较次数和记录的移动次数。
空间复杂度：分析排序算法中需要多少辅助内存。
稳定性：若两个记录A和B的关键字值相等，但排序后A、B的先后次序保持不变，则称这种算法是稳定的；反之，就是不稳定的。

1、冒泡排序

  思想：它重复地走访过要排序的数列，一次比较两个元素，小的上“冒”，大的下沉。

for (int i = 0; i < a.length; i++) { 
   
    for (int j = 0; j < a.length - 1 - i; j++) { 
   
        if (a[j] > a[j + 1]) { 
   
            int temp = a[j];
            a[j] = a[j + 1];
            a[j + 1] = temp;
        }
    }
}

2、直接插入排序

   思想：每步将一个待排序的记录按其关键字的大小插到前面已经排序的序列中的适当位置，直到全部记录插入完毕为止。
  如果输入数组已经是排好序的话，插入排序出现最佳情况，其运行时间是输入规模的一个线性函数。如果输入数组是逆序排列的，将出现最坏情况。平均情况与最坏情况一样，其时间代价是(n2)。

for (int i = 1; i < a.length; i++) { 
   
    int j = i;
    while (j > 0) { 
   
        if (a[j] < a[j - 1]) { 
   
            int temp;
            temp = a[j];
            a[j] = a[j - 1];
            a[j - 1] = temp;
            j--;
        } else { 
   
            break;
        }
    }
}

3、简单选择排序

   思想：每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。

int i, j;
for (i = 0; i < a.length; i++) { 
   
    //temp为哨兵
    int temp = a[i];
    for (j = i - 1; j >= 0 && a[j] > temp; j--) { 
   
        //逐个向后移
        a[j + 1] = a[j];
    }
    //temp插入位置
    a[j + 1] = temp;
}

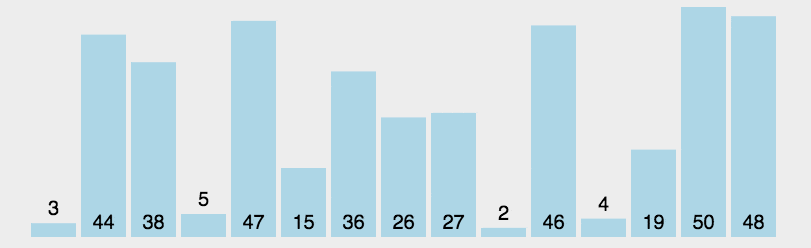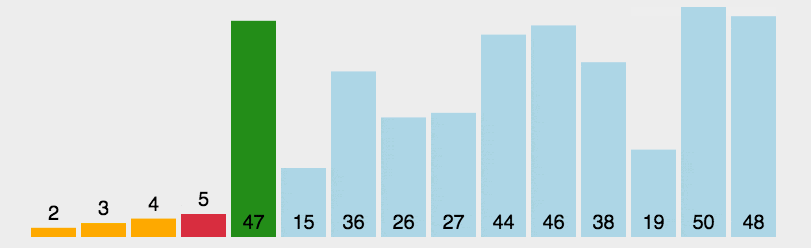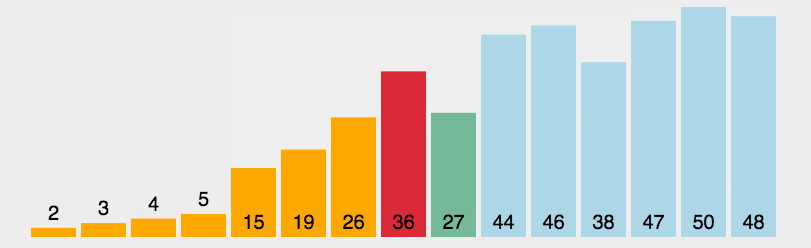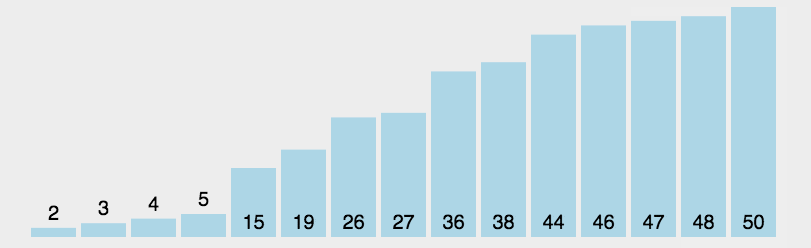
4、快速排序算法

   快速排序的原理：选择一个关键值作为基准值。比基准值小的都在左边序列（一般是无序的），比基准值大的都在右边（一般是无序的）。一般选择序列的第一个元素。
   一次循环：从后往前比较，用基准值和最后一个值比较，如果比基准值小的交换位置，如果没有继续比较下一个，直到找到第一个比基准值小的值才交换。找到这个值之后，又从前往后开始比较，如果有比基准值大的，交换位置，如果没有继续比较下一个，直到找到第一个比基准值大的值才交换。直到从前往后的比较索引>从后往前比较的索引，结束第一次循环，此时，对于基准值来说，左右两边就是有序的了。

/** * 快速排序，使得整数数组 arr 有序 */
public static void quickSort(int[] arr) { 
   
    if (arr == null || arr.length < 2) { 
   
        return;
    }
    quickSort(arr, 0, arr.length - 1);
}

/** * 快速排序，使得整数数组 arr 的 [L, R] 部分有序 */
public static void quickSort(int[] arr, int L, int R) { 
   
    if(L < R) { 
   
        // 把数组中随机的一个元素与最后一个元素交换，这样以最后一个元素作为基准值实际上就是以数组中随机的一个元素作为基准值
        swap(arr, new Random().nextInt(R - L + 1) + L, R);
        int[] p = partition(arr, L, R);
        quickSort(arr, L, p[0] - 1);
        quickSort(arr, p[1] + 1, R);
    }
}

/** * 分区的过程，整数数组 arr 的[L, R]部分上，使得： * 大于 arr[R] 的元素位于[L, R]部分的右边，但这部分数据不一定有序 * 小于 arr[R] 的元素位于[L, R]部分的左边，但这部分数据不一定有序 * 等于 arr[R] 的元素位于[L, R]部分的中间 * 返回等于部分的第一个元素的下标和最后一个下标组成的整数数组 */
public static int[] partition(int[] arr, int L, int R) { 
   

    int basic = arr[R];
    int less = L - 1;
    int more = R + 1;
    while(L < more) { 
   
        if(arr[L] < basic) { 
   
            swap(arr, ++less, L++);
        } else if (arr[L] > basic) { 
   
            swap(arr, --more, L);
        } else { 
   
            L++;
        }
    }

    return new int[] { 
    less + 1, more - 1 };

}

/* * 交换数组 arr 中下标为 i 和下标为 j 位置的元素 */
public static void swap(int[] arr, int i, int j) { 
   
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

5、希尔排序算法

   插入排序的升级版。希尔排序的中心思想是将数据进行分组，然后对每一组数据进行插入排序，在每一组数据都有序后，再对所有的分组利用插入排序进行最后一次排序。这样可以显著减少数据交换的次数，以达到加快排序速度的目的。
（1）操作方法： 选择一个增量序列t1，t2，…，tk，其中ti>tj，tk=1；
（2）按增量序列个数k，对序列进行k 趟排序；
（3）每趟排序，根据对应的增量ti，将待排序列分割成若干长度为m 的子序列，分别对各子表进行直接插入排序。仅增量因子为1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

int h = 1;
while(h <= nElem / 3) { 
   
    h = h * 3 + 1; //增量间隔
}

while(h > 0) { 
   
    for(int i = h; i < nElem; i++) { 
   
        //每个增量间隔内，实现插入排序，两个for循环和插入排序一样，只不过第二个for循环里参数略有调整而已，和h有关
        for(int j = i; j < nElem; j += h) { 
   
            for(int k = j; (k - h >= 0) && a[k] < a[k - h]; k -= h) { 
   
                swap(k, k-h);
            }
        }
    }
    h = (h-1) / 3;
}

今天的文章Java的几种经典排序算法分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。