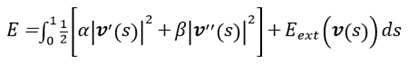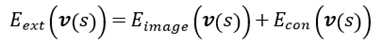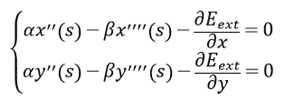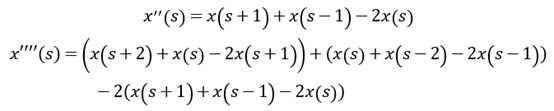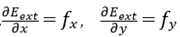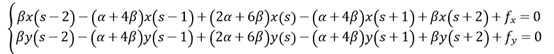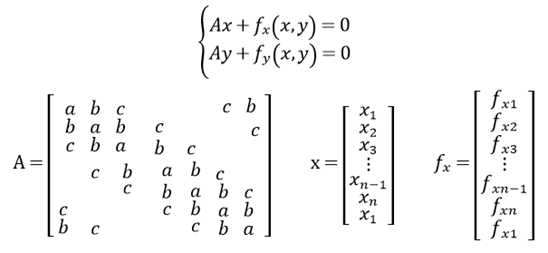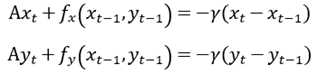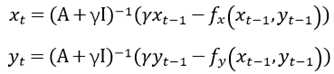Snake活动轮廓模型

1. Snake模型

        人为地在图像感兴趣的区域（ROI）上给出初始轮廓曲线，最小化一个能量函数，使轮廓曲线在图像中运动（变形），最终逼近该区域的边界。

        设v(s)=[x(s),y(s)]为活动轮廓线，s∈[0, 1]是弧长，其能量函数为：

曲线能量的第一项是曲线的一阶导和二阶导，为曲线的内部能量，其中一阶导为连续能量，控制连续；二阶导到为曲率能量，控制平滑。能量的第二项是外部能量，一般为下面的形式：

其中E_image为轮廓与图像特征之间的吻合程度，如E_image(v(s))=±[▽G_σ(x,y)*I(x, y)]²等；E_con：控制能量，来源于先验知识和用户本身。

2. Snake模型求解

由欧拉公式（变分法），使E_snake最小必须满足：

αv”(s)-βv””(s)-▽E_image(v(s))-▽E_con(v(s))=0

又v(s)=[x(s), y(s)]，上式可化为：

将导数用差分近似：

记

则

写成矩阵形式：

A为五对角循环矩阵，a=2α+6β，b=-(α+4β)，c=β 。

利用梯度下降法，可得

解得：

3. 代码

使用说明：

1.  matlab编写，需要在matlab下运行。
2. matlab文件路径下需要有一个名为 test.jpg 的 uint8 类型的二维灰度图，该图片即为需要分割的图片。
3. 运行时，在matlab命令行直接输入m文件名称，然后将会显示出  test.jpg  图片，需要在该图片上手动画出初始轮廓。画初始轮廓线时，鼠标点击图片中的几个位置，程序会以直线段的方式将这个几个点连接起来，作为初始轮廓线。画好后，关闭图片，然后在命令行按 enter 键，让程序继续运行。
4.  未设置迭代的终点，默认为400次迭代，若没有收敛自行更改迭代次数。

代码如下：

% 基本Snake活动轮廓模型

I=imread('test.jpg');   % 读入的图片应为uint8类型二维的灰度图
snake(I);			    % 对图像I求其中需要分割物体的snake边界

function snake(I)
% Snake主体部分

alpha=0.5; beta=0;      % 连续参数alpha=0.5；平滑参数beta=0；步长为1
[x,y]=DrawLine(I);	% 在图像I上手动画线，得到初始轮廓线

a=2*alpha+6*beta; b=-(alpha+4*beta); c=beta;
J=[c b a b c]; h=max(size(x));
A=diagCyclMat(h,J);     % 求取设定参数下的五对角循环矩阵

II=eye(h); [m,~]=size(I);        % 初始化
I=double(I);

I1=-ff(I);                       % 高斯势能I1
[I2x,I2y]=NGradient(I1);         % I1的负梯度I2
T=max(max(abs(I2x(:))),max(abs(I2y(:))));
I2x=I2x/T; I2y=I2y/T;            % 梯度归一化
fx=-1*I2x; fy=-1*I2y;            % f为图像I的高斯势能的梯度


for t=1:400                      % 迭代，未计算迭代终点   
    ffx=fx(m*(uint16(x)-1)+uint16(y));
    ffy=fy(m*(uint16(x)-1)+uint16(y));
    x=((II/(A+II))*(x'-ffx'))';
    y=((II/(A+II))*(y'-ffy'))';
end

I=uint8(I); imshow(I);  hold on
plot(x,y,'Color','White')         % 显示最终Snake轮廓线
end

function I1=ff(I)
%求取I的边缘函数（负高斯势能）

%5阶Standard Deviation=3的高斯滤波，sobel梯度
h=fspecial('gaussian',5,3); w1=fspecial('sobel'); w2=w1';

Is=imfilter(double(I),h,'conv','replicate');
I1=imfilter(Is,w1,'replicate').^2+imfilter(Is,w2,'replicate').^2;

end

function [I2x,I2y]=NGradient(I)
%求取I的负梯度
%sobel梯度
w1=fspecial('sobel'); w2=w1';
I=double(I);
I2y=imfilter(I,w1,'replicate');
I2x=imfilter(I,w2,'replicate');
end

function A=diagCyclMat(n,J)
% A = diagonal cycle(J) matrix.
%生成一个以向量J为循环体的对角循环矩阵
%2017.10.27 
l=length(J); h=(l+1)/2;
if n<l
    error('A is too small to hold J');
end
if mod(l,2)==0
    error('length.J is not odd');
end
A=zeros(n);
for i=1:n
    j=i;
    A(i,j)=J(h);
    k=1;
    while (h-k)~=0
        if (j-k)<1
            j=j+n;
        end
        A(i,j-k)=J(h-k);
        k=k+1;
    end
    k=1;
    while (h+k)~=l+1
        if (j+k)>n
            j=j-n;
        end
        A(i,j+k)=J(h+k);
        k=k+1;
    end
end
end

function [x,y]=DrawLine(I)

imshow(I)
hold on
tag=0; P=zeros(2); LX=[]; LY=[];
set(gcf,'WindowButtonDownFcn',@DoLine);
pause;
x=LX; y=LY;

function DoLine(~,~)
pt=get(gca,'CurrentPoint');
if tag==0
    P(1,1)=pt(1,1); P(1,2)=pt(1,2);
    tag=1;
else
    P(2,1)=pt(1,1); P(2,2)=pt(1,2);
    LinkLine(P);
    P(1,1)=P(2,1); P(1,2)=P(2,2);
end
end

function LinkLine(P)
xh=abs(P(2,1)-P(1,1));
yh=abs(P(2,2)-P(1,2));
if yh>xh
    n=int16(yh+1);
    k=double((P(2,1)-P(1,1))/(P(2,2)-P(1,2)));
    k1=(P(2,2)-P(1,2))/yh;
    X=zeros(1,n);Y=zeros(1,n);
    for i=1:n
        Y(i)=P(1,2)+(i-1)*k1;
        X(i)=P(1,1)+ceil((i-1)*k1*k);
    end
else
    n=int16(xh+1);
    k=double((P(2,2)-P(1,2))/(P(2,1)-P(1,1)));
    k1=(P(2,1)-P(1,1))/xh;
    X=zeros(1,n);Y=zeros(1,n);
    for i=1:n
        X(i)=P(1,1)+(i-1)*k1;
        Y(i)=P(1,2)+ceil(k*k1*(i-1));
    end
end
LX=[LX X]; LY=[LY Y];
plot(LX,LY,'Color','Red')
hold on
end

end

今天的文章Snake活动轮廓模型分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。