1、Snake算法原理

Kass等人¹最早于1988年提出了主动轮廓模型，该方法通过构造能量函数，从而将图像分割转化为求解能量泛函极值的问题，其核心思想在于，作者认为和之前的分割方法相比，在不同的图像解读(image interpretation)任务中，表观或者浅层次(low level)的图像判读任务应该需要一些深层次(high level)的图像信息，并论文[1]中进行了举例分析，有兴趣的同学可以自行翻阅论文查看，这也和主动轮廓模型的两大特点不谋而合：全局性和可拓展性。全局性也就是说在图像处理任务进行中，不仅要关注局部区域或者边缘信息，同样也要关注图像或曲线的整体信息如曲线整体的长度和曲率等。再者针对不同的图像特点，能够设计或者添加个性化的分割策略，接下来我将根据公式对此进一步分析。
对于图像$I(x,y),C(s)=C(x(s),y(s))$为演化曲线，定义snake模型的能量函数为：$$E_{snake}=E_{int}+E_{ext}$$ 这里我们区分内部能量和外部能量的依据就是看它是否和演化曲线本身的特性相关。比如说下式中，定义内部能量项的两部分内容分别代表的就是曲线的长度和曲率： $$E_{int}={\int }_0^1\frac{1}{2}\ast (\alpha (s)|c_s(s){|}^2+\beta (s)|c_{ss}(s){|}^2)\mathrm{d}s$$ 其中公式中的两项内容分别表示的就是曲线的长度项和曲线的光滑程度, $\alpha (s)$和$\beta (s)$可以根据曲线上某一点的特征进行个性化处理，但是大多数情况下我们一般定义它们为常数,用于调节曲线长度项和光滑程度占比。
而外部能量项通常由两部分组成构成：$$E_{ext}=E_{img}+E_{cons}$$ $E_{img}$通常表示和图像相关的外部能量项目，主要包含如下三种信息，
(1)

1. 图像的像素信息(Line functional): $$E_{line}={\int }_0^{1}I(x(s),y(s))\mathrm{d}s$$
2. 图像的梯度信息(edge functional)(注意负号):$$E_{edge}={\int }_0^1-|\nabla I(x(s),y(s))\mathrm{d}s$$，
3. 或者曲线周围小范围空间的梯度信息(scale space):$$E_{line}={\int }_0^1-g_{\delta }\ast {\nabla }^{2}I(x(s),y(s))\mathrm{d}s$$在实际使用中图像的梯度信息$E_{edge}$使用的较为广泛，以及后面的实现过程中，我们也会用$E_{edge}$作为图像力，负号的作用就在于,在边缘梯度较大的情况下,整体的能量泛函越小,曲线也就更加趋向于演化到图像的边缘位置。

最后还有一个限制项$E_{con}$，这一项就是对曲线演化添加一定的限制作用,比如限制整体曲线到某一点或者某一区域$R$的距离:$$E_{c}on={\int }_0^1||C(x(s),y(s))-R||\mathrm{d}s$$具体的情况大家可以根据图片特点或者需求灵活定义。

2、基于曲线演化的实现方法

好了，终于到了激动人心的实现环节了，大家是不是跟我一样激动的直搓手，哈哈哈哈哈哈哈
开始之前我先说明两点内容：1)本次实现过程基于较为简单基础的能量泛函，大家可以先实现体验一边，然后再触类旁通，举一反三；2)以方面需要对一些数学知识进行回顾分析，另一方面希望大家仔细品一品从连续到离散的变化过程。

2.1演化方程推导

首先我们定义能量函数:$$E_{snake}={\int }_0^1\frac{1}{2}\ast (\alpha |c_s(s){|}^2+\beta |c_{ss}(s){|}^2-|\nabla I(x(s),y(s)){|}^2)\mathrm{d}s$$,当能量函数最小时，就可以获得$C(x(s),y(s))$的曲线方程，本质上这也是一个求能量泛函极值的问题，直接根据欧拉-拉格朗日方程(变分原理)，当能量泛函取极值时，应满足：$$-\alpha c^{{}^{\prime \prime }}(s)+\beta c^{{}^{\prime \prime \prime \prime }}(ss)+\nabla E_{ext}=0$$ 可是就算推到这种程度我们以然没办法直接求出曲线$c(x(s),y(s))$,尤其是我们希望公式能够以偏微分方程的形式出现，这样我们就可以利用计算机进行编程序迭代计算了，于是我们在曲线中引入了一个辅组变量$t$，则解可以表示为$c(t,s)$,随时间变化的解$c(t,s)$应该使得能量函数逐渐变小(推导过程后续会补充),从而可以得出:$$\frac{\partial c(s)}{\partial t}=\alpha c^{{}^{\prime \prime }}(s)-\beta c^{{}^{\prime \prime \prime \prime }}(ss)-\nabla E_{ext}$$

2.2离散化过程

接下来就是整个离散化过程了,首先,我们先明确一下概念，上式中的$s$表示什么意思，因为我们看到的图片都是离散的点，所以我们刚开定义初始化的snake曲线时，实际上定义的也就是一系列离散的点的集合，而曲线的演化过程实际上也就是这些固定数目的点的演化过程，离散化后，我们用$i$表示$s$,那假设初始化的snake曲线有$N$个点，那$i\in [0,N-1]$,且$x[N]=x[0],x[N+1]=x[2]....$,那么对于曲线上任一点$c(x(i),y(i))$：$$x^{{}^{\prime \prime }}[i]=x[i-1]-2x[i]+x[i+1]$$ $$x^{{}^{\prime \prime \prime \prime }}[i]=x[i-2]-4x[i-1]+6x[i]-4x[i+1]+x[i+2]$$对y也是同理，假设图像$x$方向和$y$方向的梯度为$G(x,y)$(均为正值),那外部力则分别为$G_x[x,y],G_y[x,y]$,假定每次迭代后,曲线变化较小,我们用$G_{t-1}(x,y)$代替$G_t(x,y)$,那么对任一点$c(x(i),y(i))$就可以推导出离散后的公式为:
$$\frac{\partial x_t[i]}{\partial t}=\alpha (x_t[i-1]-2xt[i]+x_t[i+1])+\beta (-x_t[i-2]+4x_t[i-1]-6xt[i]+4x_t[i+1]-x_t[i+2])+G_x(x_t[i],y_t[i])$$用$\lambda$表示步长,则可以进一步表示为：$$\frac{x_t[i]-x_{t-1}[i]}{\lambda }=\alpha (x_t[i-1]-2xt[i]+x_t[i+1])+\beta (-x_t[i-2]+4x_t[i-1]-6xt[i]+4x_t[i+1]-x_t[i+2])+G_x(x_{t-1}[i],y_{t-1}[i])$$同理， $$\frac{y_t[i]-y_{t-1}[i]}{\lambda }=\alpha (y_t[i-1]-2yt[i]+y_t[i+1])+\beta (-y_t[i-2]+4y_t[i-1]-6yt[i]+4y_t[i+1]-y_t[i+2])+G_y(y_{t-1}[i],y_{t-1}[i])$$ ,如果一条曲线上有$N$个点，那就对$x$和$y$分别列出$N$个式子，如果用矩阵表示的话，那就是:$$\frac{X_t-X_{t-1}}{\lambda }=A{X}_t+G_x(x_{t-1},y_{t-1})$$矩阵A则为：$$\left(\begin{array}{cccccccccc}-2\alpha +6\beta & \alpha +4\beta & -\beta & 0& 0& 0& \cdots & -\beta & \alpha +4\beta & \\ \alpha +4\beta & -2\alpha +6\beta & \alpha +4\beta & -\beta & 0& 0& \cdots & 0& -\beta & \\ -\beta & \alpha +4\beta & -2\alpha +6\beta & \alpha +4\beta & -\beta & 0& \cdots & 0& 0& \\ 0& -\beta & \alpha +4\beta & -2\alpha +6\beta & \alpha +4\beta & -\beta & \cdots & 0& 0& \\ 0& 0& -\beta & \alpha +4\beta & -2\alpha +6\beta & \alpha +4\beta & \cdots & 0& 0& \\ ⋮& ⋮& ⋮& \ddots & ⋮& & & & & \\ -\beta & 0& 0& 0& 0& 0& \cdots & -2\alpha +6\beta & \alpha +4\beta & \\ \alpha +4\beta & -\beta & 0& 0& 0& 0& \cdots & \alpha +4\beta & -2\alpha +6\beta & \end{array}\right)$$，求解矩阵即可得出：$$X_t=(1-\lambda A{)}^{-1}{X}_{t-1}+\lambda G_x(X_{t-1},Y_{t-1})$$ $$Y_t=(1-\lambda A{)}^{-1}{Y}_{t-1}+\lambda G_y(X_{t-1},Y_{t-1})$$至此，需要的核心演化公式到手。

2.3 代码实现

看完上面的离散化过程，是不是大家现在都胸有成竹，跃跃欲试，蠢蠢欲动啦，哈哈，接下来就让我们一起开始愉快的coding吧。
声明使用的依赖库主要有：

import numpy as np
import cv2
import matplotlib.pyplot as plt
from pylab import*
import skimage.filters as filt

代码实现总共分为如下几个步骤：

1. 读入图片：
   随手用windows画图工具画了个圆(简约派)：
   
   然后读入图片，注意

Image = cv2.imread('xxx.bmp',1)
image = cv2.cvtColor(Image,cv2.COLOR_BGR2GRAY)
img = np.array(image,dtype = np.float)
plt.imshow(img,cmap = 'gray') # 读入灰度图
print(shape(img))

2. 定义初始化snake曲线,注意 注意 注意，此处我们需要首先明确x，y分别表示矩阵的列和行，同时也就意味着绘图的时候x，y分别表示x-y坐标系的横坐标轴和纵坐标轴呀，一定要品明白哈，不然会出大问题的哈(说多了都是泪)

t = np.linspace(0,2*np.pi,60,endpoint = True)
y = 100+30*np.cos(t)
x = 100+30*np.sin(t)

3. 然后定义关键参数，部分参数值参考原论文：

alpha = 0.001
beta  = 0.4
gamma = 100 # 迭代步长
sigma = 20  # 滤波用的高斯分布参数
iterations = 300 # 迭代次数

4. 计算矩阵，有没有发现整个矩阵只由参数控制，而和图片无关：

N = np.size(x)
a = gamma*(2*alpha+6*beta)+1
b = gamma*(-alpha-4*beta)
c = gamma*beta

p = np.zeros((N,N),dtype=np.float)
p[0] = np.c_[a,b,c,np.zeros((1,N-5)),c,b]
print(p[0].shape)
for i in range(N):
    p[i] = np.roll(p[0],i)
p = np.linalg.inv(p)

5. 计算外部力，因为手绘图像噪声较小，很难直接通过梯度产生外部力，因此先对图像进行高斯滤波处理，注意此处的卷积核和高斯分布参数都选择的较大，大家可以品一品为什么要这样做：

smoothed = cv2.GaussianBlur((img-img.min()) / (img.max()-img.min()),(89,89),sigma)
giy,gix  = np.gradient(smoothed)
gmi = (gix**2+giy**2)**0.5
gmi = (gmi - gmi.min()) / (gmi.max() - gmi.min())
Iy,Ix = np.gradient(gmi)

6. 定义函数，确保演化曲线不超出图像边界，并返回整数形位置信息：

def fmax(x,y):
    x[x < 0] = 0
    y[y < 0] = 0
    x[x > img.shape[1]-1] = img.shape[1]-1
    y[y > img.shape[0]-1] = img.shape[0]-1
    return y.round().astype(int),x.round().astype(int)

7. 迭代计算，并显示图像：

plt.plot(y,x,'.')
for i in range(iterations):
    fex = Ix[fmax(x,y)]
    fey = Iy[fmax(x,y)]
    x = np.dot(p,x+gamma*fex)
    y = np.dot(p,y+gamma*fey)
    if i%10 ==0:
        plt.plot(x,y,'.')
plt.show()

计算结果，撒花，撒花，撒花！

3、基于水平集的实现方法

本来这一段打算拖一拖的，但是看到评论区有哥们儿问到了，我就仔细找了找文献，看看怎么给处理下，结果发现自己给自己挖了个大坑，对于原始的snake算法来讲，使用level set并不是一个很可行的方案或者说需要对snake算法做一些改变，那么为什么将level set方法直接引用到snake模型上不合适呢？
1）首先，大家需要明白常见的主动轮廓模型的常见处理流程：1、构建能量泛函; 2、极小化能量泛函(欧拉-拉格朗日方程+梯度下降法)获得用于演化的偏微分方程; 3、离散化偏微分方程; 4、代码实现与调试，一般都是从步骤1或者步骤2中引入level set，可以参见我的另一篇博客(水平集方法引入主动轮廓模型算法中的两种方法)；2）但是，对于原始的snake算法来讲，只存在从步骤1即从能量函数中引入水平集函数的可能性，不过因为那样可能处理起来太麻烦，所以后来Caselles 等人就在1993年直接对原始snake算法就行了调整，提出了改进的几何活动轮廓模型，不仅引入了水平集方法还摆脱了原始snake模型对参数的依赖问题。
因此，总的来说，将level set方法引入snake是理论上的可行性的，只不过比较麻烦，这个博主最近时间比较紧张，等过一段时间闲了再想办法给实现下吧(又立flag…)。

4、讨论与分析

接下来就让我们愉快的讨(tu)论(cao)下snake算法吧！ 有一说一，不得不承认，Kass等人¹当初将图像分割问题转化为求解能量泛函极值的问题确实很有想象力，这个控制领域的李雅普诺夫函数简直有异曲同工之妙之妙，很好奇当时作者哪来的这么大的脑洞哈。

1. 先说优点，因为能量函数的构造方式，就决定了这种方法具有很好的扩展性，这也是主动轮廓模型能够针对具体应用问题不断改进的重要原因；
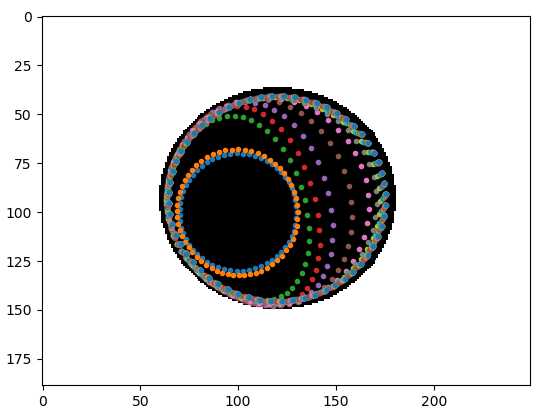
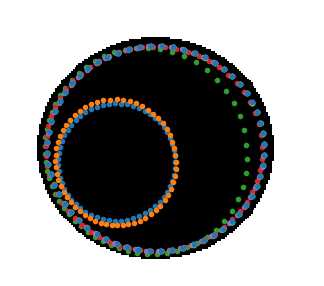
2. 但是缺点也很明显：1）snake模型太过于依赖参数，针对不同的图像图像都需要找出”合适的参数”才能完美的分割轮廓，大家可以尝试在代码中调试参数值就会有所体会，甚至减少初始演化点的个数都会导致演化失败，如下两图分别是相同参数，初始时设定60个演化点和30个演化点的演化结果区别，，在不改变图像及参数的情况下，仅仅因为演化点个数减少，演化结果就迥然不同，这就凸显了snake模型对参数的依赖性以及算法较差的鲁棒性，这显然不能符合实际应用需求。因此后来Caselles等人²提出了几何活动轮廓模型对snake进行了改进：1)曲线能够自动地根据图像特征如梯度而不是依赖人工设定参数演化到目标边缘；2)引入了水平集方法，用面的演化代替了点的演化，并且使得图像能够处理拓扑结构的变化。

源码地址snake

[1] (KASS,M. snake Active contour models[J]. Proc.first Intl Conf.computer Vision, 1988, 4.)

[2] (Caselles V . Geometric models for active contours[C]// International Conference on Image Processing. IEEE Computer Society, 1995.)今天的文章基于边缘的主动轮廓模型——从零到一用python实现snake分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。