模型:一条可变形的参数曲线及相应的能量函数,以最小化能量函数为目标,控制参数曲线变形,具有最小能量的闭合曲线即是目标轮廓。
snake模型调和了上层知识和底层图像特征矛盾。
上层知识指物体形状。表示内部力。
底层图像特征是局部的,如亮度、梯度等,即这些特征仅与像素所在领域有关,与物体形状无关。表示外部力或称图像力。
曲线的形变同时受作用在模型上许多不同力控制,每种力产生一部分能量,这部分能量表示为能量函数一个独立的能量项。
V(s) = [ x(s) , y(x) ] , s∈[0, 1]
s是以傅里叶变换形式描述边界的自变量。
能量函数:

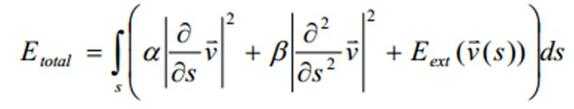
第一项为弹性能量,第二项为弯曲能量,组成内部力,第三项为外部能量,组成外部力(图像力)。
外部能量通常取控制点或连线所在位置的局部图像特征,如梯度。

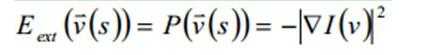
当轮廓靠近目标图像边缘,梯度增大,上式能量最小,则速度变为0,停止运动。
内部力用于控制轮廓线弹性形变,保持轮廓连续性和平滑性。
外部力用于使变形曲线与图像局部特征相吻合。
内部能量仅跟形状有关;外部能量仅跟图像数据有关。
α、β决定伸展弯曲的程度。
求解:
对图像的分割转化为能量函数极小化。
弹性能量把轮廓线压缩成一个圆,弯曲能量驱使轮廓线成为光滑曲线或直线,外部能量使轮廓线向图像高梯度靠拢。
由于图像上的点是离散的,能量函数的算法必须在离散域里定义,求解能量函数极小值即是
变分问题。
变分问题。
通过欧拉方程求解,欧拉方程是泛函极值的微分表达式,求解泛函的欧拉方程,即可得到使能量函数取极小值的驻函数,将变分问题转化为微分问题。
今天的文章snake主动轮廓模型分享到此就结束了,感谢您的阅读,如果确实帮到您,您可以动动手指转发给其他人。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/27773.html
