沙猫群优化算法(Sand Cat Swarm Optimization,SCSO)(附改进及Matlab源码,完整,免费)
一、算法灵感
沙猫群优化(Sand Cat Swarm Optimization, SCSO)算法是一种受自然界沙猫行为而设计的元启发式算法。沙猫的两个主要动作是觅食和攻击猎物。这个算法的灵感来源于沙猫对低频噪声的检测能力。沙猫无论是在地面上还是在地下,都能凭借其独特的特征找到猎物。
二、算法介绍
2.1 初始化
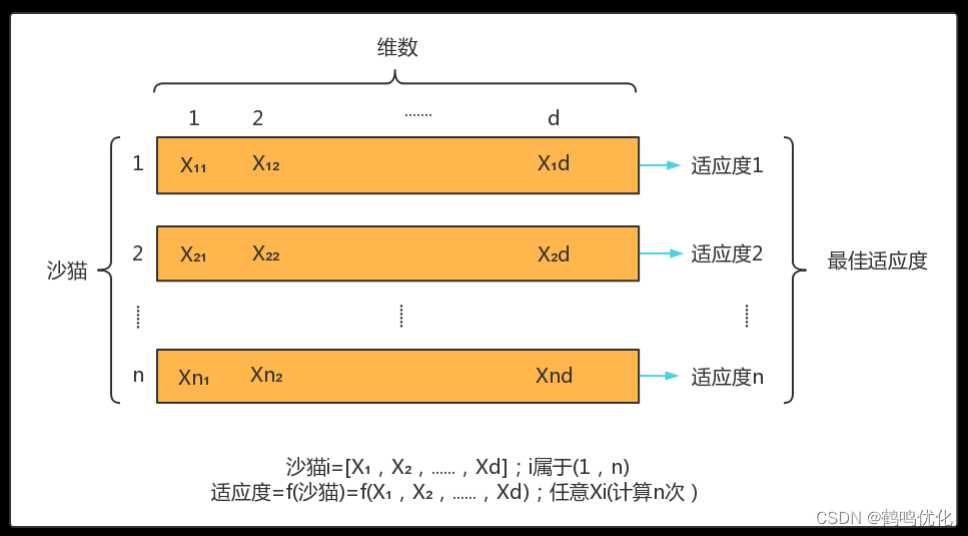
该算法是一种基于种群的方法,将相关结构定义为向量。在 d d d 维优化问题中,沙猫是表示问题解的 1 × d 1×d 1×d 数组,其定义如图1所示。每个变量值 ( x 1 , x 2 , … , x d ) (x_1, x_2, …, x_d) (x1,x2,…,xd)都是一个浮点数。在这里,每个 x x x 必须位于下界和上界之间。在初始化算法中,首先,根据问题的大小 ( N p o p × N d ) (N_{pop} × N_d) (Npop×Nd), ( p o p = 1 , … , n ) (pop = 1,…,n) (pop=1,…,n)用沙猫种群创建一个候选矩阵。每只沙猫的适应度通过待解决问题的适应度函数得到。
图1 沙猫初始化过程
2.2 搜索猎物(探索阶段)
控制探索与开发阶段过渡的最终参数和主要参数是 R R R,当 ∣ R ∣ > 1 \left| R \right| > 1 ∣R∣>1 时,沙猫对进行猎物搜索。沙猫对猎物的搜索依赖于低频噪声的释放,假设沙猫的灵敏度范围 r G {r_G} rG 从 0 0 0 到 2 2 2 kHz。 S M S_M SM 灵感来自沙猫的听觉特征,假设其值为 2 2 2。 i t e r c ite{r_c} iterc 为当前迭代, i t e r max ite{r_{\max }} itermax 为最大迭代, r a n d ( 0 , 1 ) rand(0,1) rand(0,1) 表示 0 0 0 到 1 1 1 的随机数。
r G = s M − s M × i t e r c i t e r m a x (1) {r_G} = {s_M} – {
{
{s_M} \times {iter_c}} \over {
{
{iter}_{
{
{max}}}}}} \tag{1} rG=sM−itermaxsM×iterc(1) R = 2 × r ⃗ G × r a n d ( 0 , 1 ) − r ⃗ G (2) R = 2 \times {\vec r_G} \times rand(0,1) – {\vec r_G} \tag{2} R=2×rG×rand(0,1)−rG(2) r = r G × r a n d ( 0 , 1 ) (3) r = {r_G} \times rand(0,1) \tag{3} r=rG×rand(0,1)(3)
每只沙猫根据最佳候选位置( P o s b c Po{s_{bc}} Posbc)和当前位置( P o s c Po{s_{c}} Posc)及其灵敏度范围( r r r)更新自己的位置。因此,沙猫能够找到其他可能的最佳猎物位置。
P o s ( t + 1 ) = r ⋅ ( P o s b c ( t ) − r a n d ( 0 , 1 ) ⋅ P o s c ( t ) ) (4) Pos\left( {t + 1} \right) = r \cdot \left( {Po{s_{bc}}\left( t \right) – rand\left( {0,1} \right) \cdot Po{s_c}\left( t \right)} \right) \tag{4} Pos(t+1)=r⋅(Posbc(t)−rand(0,1)⋅Posc(t))(4)
2.3 攻击猎物(开发阶段)
当 ∣ R ∣ ≤ 1 \left| R \right| \le 1 ∣R∣≤1 时,沙猫进行攻击猎物。首先,利用最佳位置 P o s b c Po{s_{bc}} Posbc 与当前位置 P o s c Po{s_{c}} Posc 来生成一个随机位置。假设沙猫的灵敏度范围是一个圆,利用轮盘赌法给每一只沙猫随机选择一个角度 θ \theta θ,最后通过公式(6)实现攻击猎物。其中,随机位置可以确保沙猫靠近猎物,随机角度可以避免算法陷入局部最优。
P o s r n d = ∣ r a n d ( 0 , 1 ) ⋅ P o s b ( t ) − P o s c ( t ) ∣ (5) Po{s_{rnd}} = \left| {rand(0,1) \cdot Po{s_b}(t) – Po{s_c}(t)} \right| \tag{5} Posrnd=∣rand(0,1)⋅Posb(t)−Posc(t)∣(5) P o s ( t + 1 ) = P o s b ( t ) − r ⃗ ⋅ P o s r n d ⋅ cos ( θ ) (6) Pos\left( {t + 1} \right) = Po{s_b}(t) – \vec r \cdot Po{s_{rnd}} \cdot \cos (\theta ) \tag{6} Pos(t+1)=Posb(t)−r⋅Posrnd⋅cos(θ)(6)
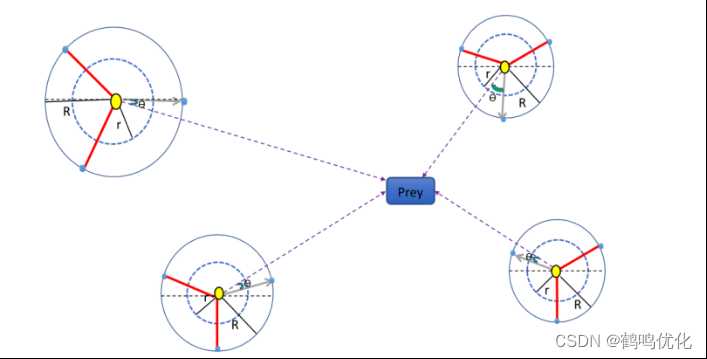
图2 沙猫群在 t 次迭代的位置
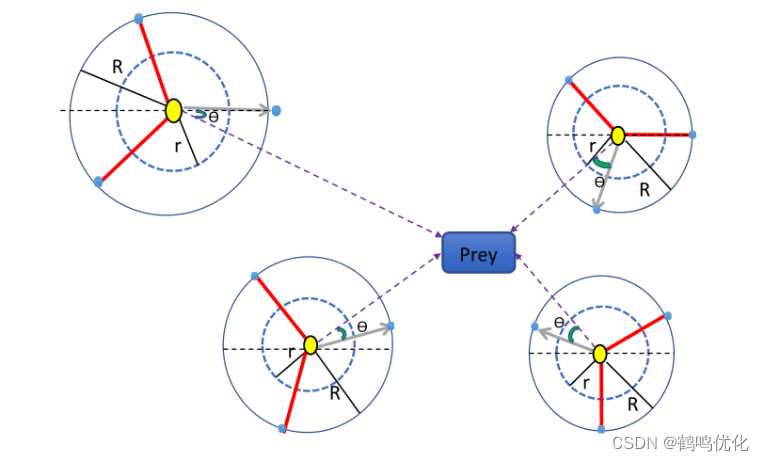
图3 沙猫群在 t +1次迭代的位置
2.4 算法伪代码
- 初始化沙丘猫数量 N N N 和最大迭代次数 T T T 等
- 初始化种群: P o s i ( i = 1 , 2 , . . . , N ) Pos_i(i=1,2,…,N) Posi(i=1,2,…,N)
- While t < = T t<=T t<=T do
- 更新 r r r、 r G r_G rG、 R R R
- 检查是否有沙丘猫超出了搜索空间并进行修改
- 计算每只沙丘猫的饥饿值(适应度值),并找到吃的最饱的沙丘猫 ( P o s b c ) (Pos_{bc}) (Posbc)
- For i = 1 i=1 i=1 to N N N do
- 利用轮盘选择算法获得随机角度 ( 0 º ≤ θ ≤ 360 º ) (0º≤\theta≤360º) (0º≤θ≤360º)
- If ∣ R ∣ < = 1 |R|<=1 ∣R∣<=1 then
- 根据等式(6)更新沙猫的搜索位置。
- Else
- 根据等式(4)更新沙猫的搜索位置。
- End If
- End For
- t = t + 1 t=t+1 t=t+1
- End While
- 返回吃的最饱的猫(最优解) P o s b c Pos_{bc} Posbc
三、实验结果
SCSO在23个经典测试函数(设置维度 d i m = 30 dim=30 dim=30)的F3、F6、F9中的收敛曲线,测试函数公式如下:
| 函数 | 公式 | 理论值 |
|---|---|---|
| F3 | F 3 ( x ) = ∑ i = 1 n ( ∑ j − 1 i x j ) 2 {F_3}(x) = \sum\nolimits_{i = 1}^n { { {(\sum\nolimits_{j – 1}^i { {x_j}} )}^2}} F3(x)=∑i=1n(∑j−1ixj)2 |
0.00 0.00 0.00 |
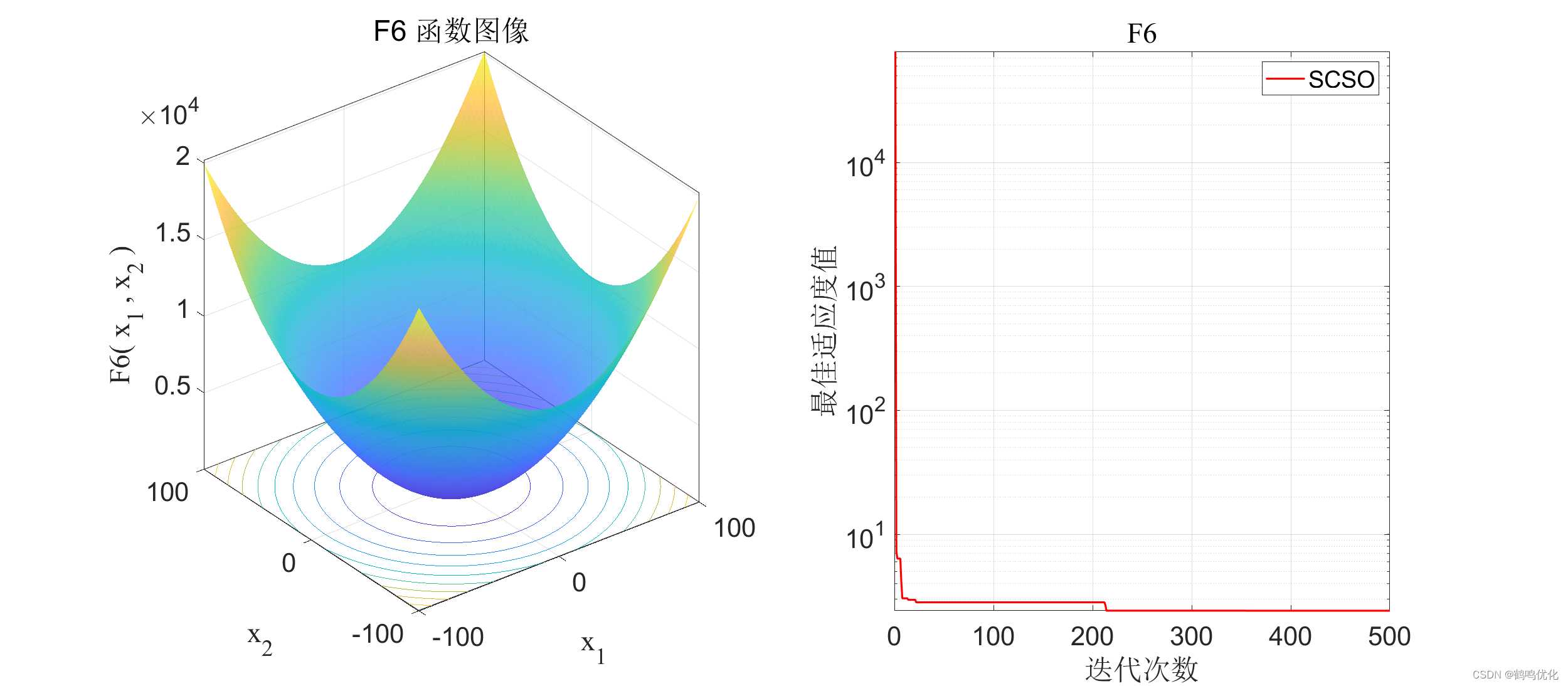
| F6 | F 6 ( x ) = ∑ i = 1 n ( x i + 5 ) 2 {F_6}(x) = {\sum\nolimits_{i = 1}^n {({x_i} + 5)} ^2} F6(x)=∑i=1n(xi+5)2 | 0.00 0.00 0.00 |
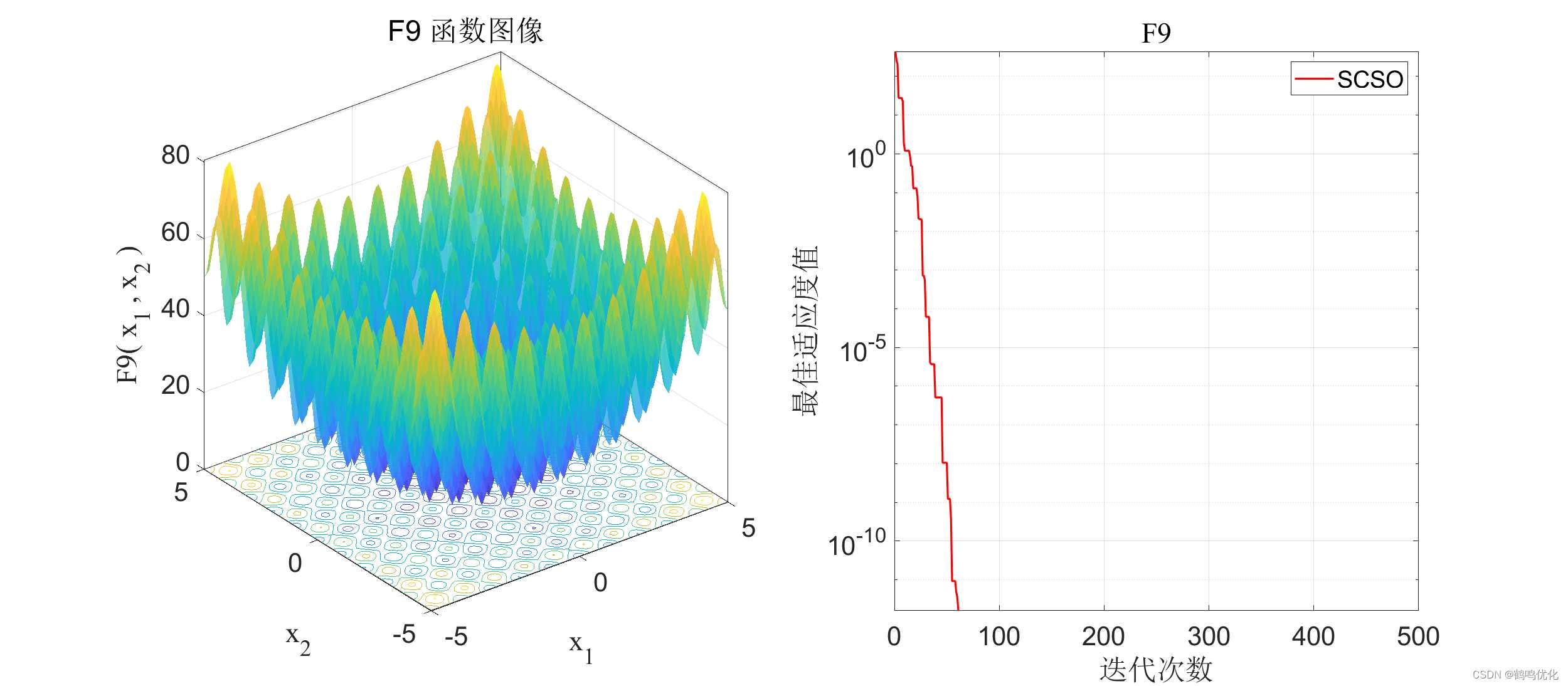
| F9 | F 9 ( x ) = ∑ i = 1 n [ x i 2 − 10 cos ( 2 π x i ) + 10 ] {F_9}(x) = \sum\nolimits_{i = 1}^n {[x_i^2 – 10\cos (2\pi {x_i}) + 10]} F9(x)=∑i=1n[xi2−10cos(2πxi)+10] | 0.00 0.00 0.00 |
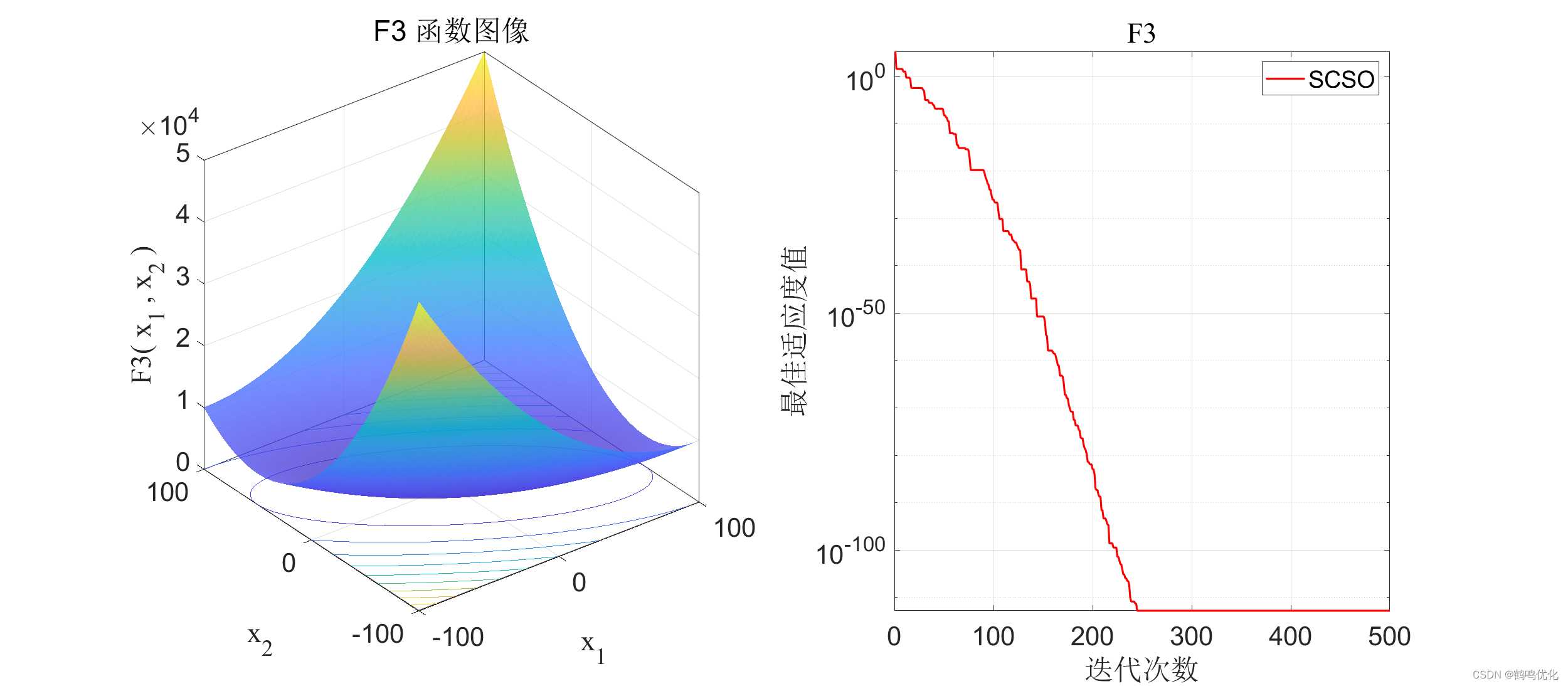
3.1 F3收敛曲线
3.2 F6收敛曲线
3.3 F9收敛曲线
四、改进沙猫群优化算法
点这里:改进的沙猫群优化算法(Modified Sand Cat Swarm Optimization,MSCSO)
五、Matlab代码
代码在资源中,可自行免费下载。
快速跳转:RSA源代码
SO源代码
SCSO源代码
六、参考文献
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/28993.html