多项式微分
- 多项式微分求解方法-ployder()
对于多项式:
其微分为：
在matlab中用行向量表示多项式，例如：
多项式
可表示为:
p 多项式微分：polyder()
其微分表达式为：
>> ployder()为求解多项式微分的函数
2. 多项式函数值求解-polyval()
对于多项式：
在区间[-2,5]上的函数图像为：
a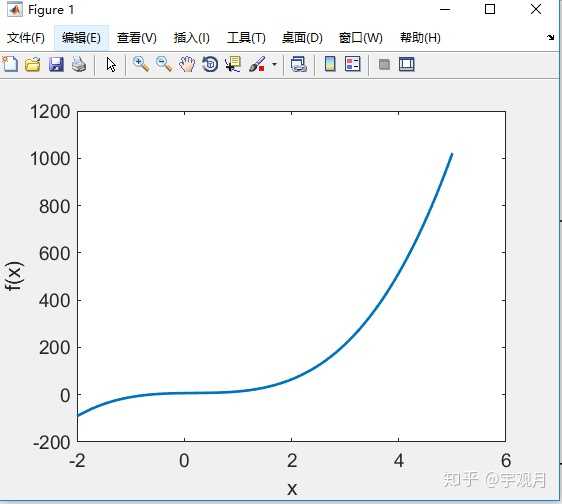 
3. 计算函数一阶导数的函数值
有函数：
求
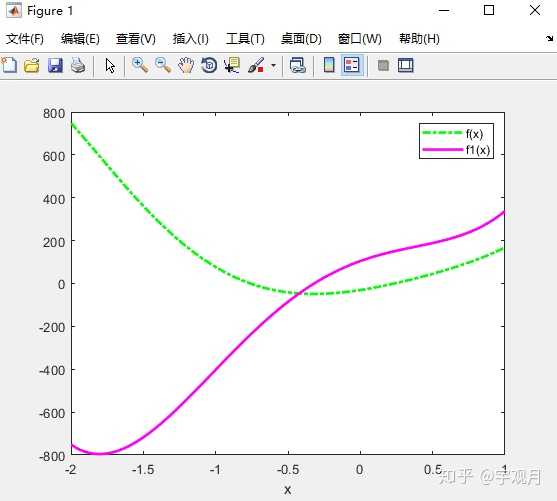
>> 4. 练习：绘制出函数
及其一阶导数的函数曲线。
x 其中，conv()用于计算多项式乘法
多项式积分
- 对于多项式：
其积分为：
2. matlab中多项式积分：polyint()
求函数
,常数项为3时的积分，以及x=7时积分函数的值。
>> 数值微分
1 函数在某一点处的斜率：
2 计算相邻元素之间的差分 :diff()
>> 3 计算两点(1, 5)和(2, 7)之间连线的斜率
>> 4 用diff()求数值微分
求函数f(x)在π/2处的一阶导数值。
>> 变化量h对一阶导数值误差的影响：
>> 5. 求函数sin(x)在区间[0,2π]上的导函数sin'(x)
hold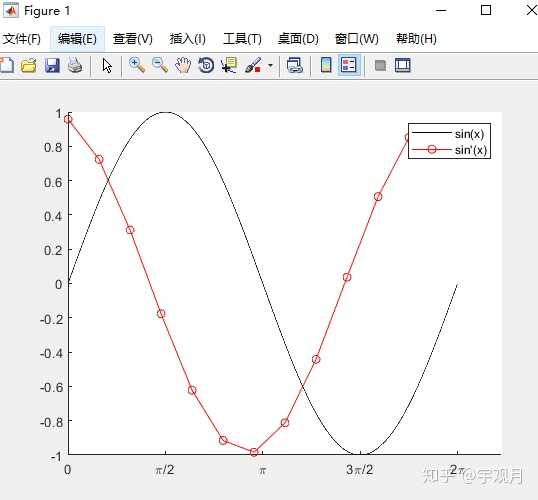 
%取不同的h值时，sin(x)的导函数
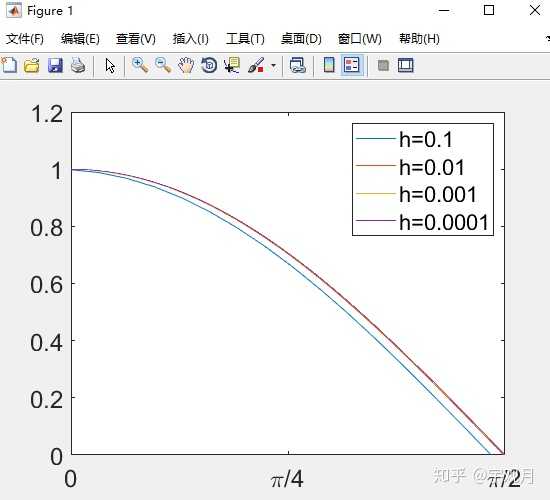
练习：h取不同值时，函数
的微分。
g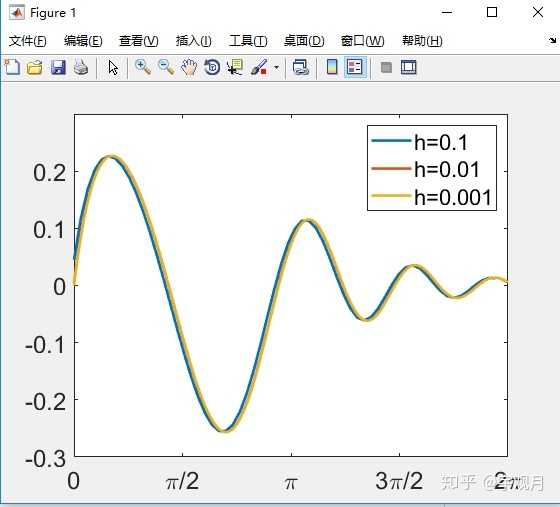 
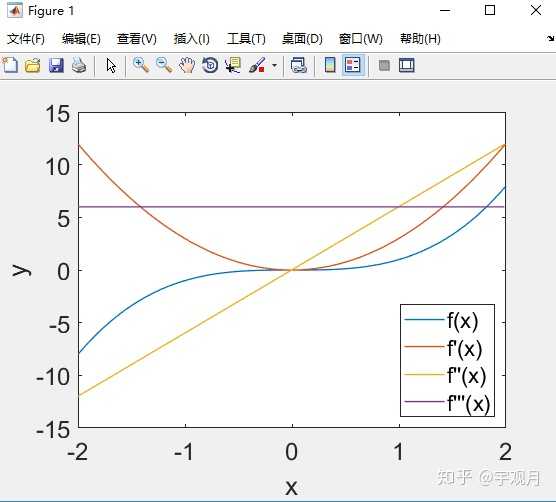
6. 二阶及三阶导数
%求函数x^3的二阶及三阶导数
数值积分
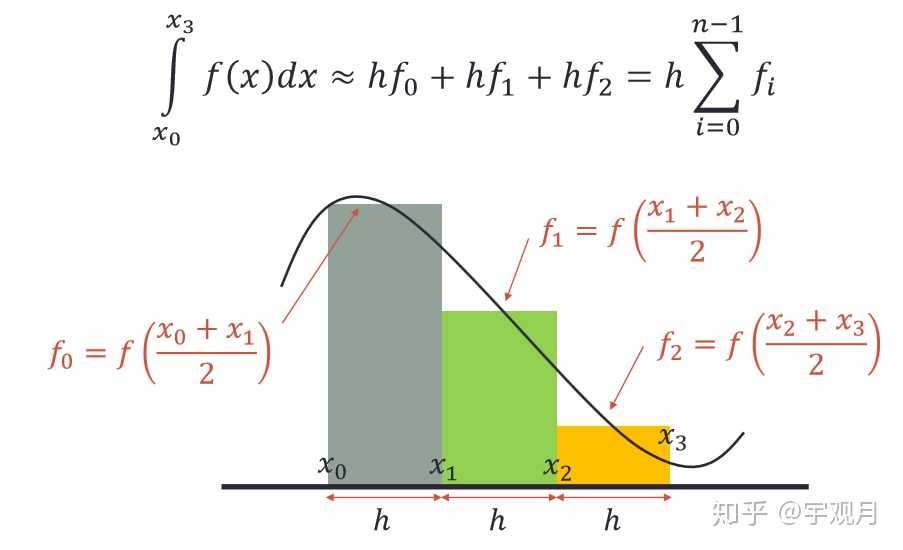
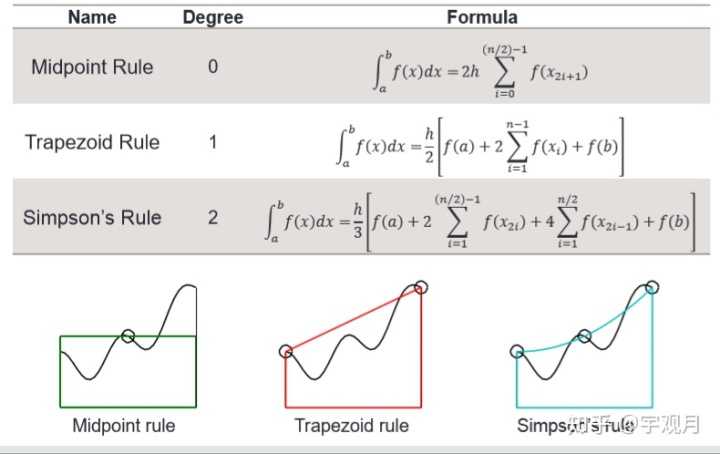
1.中点法则
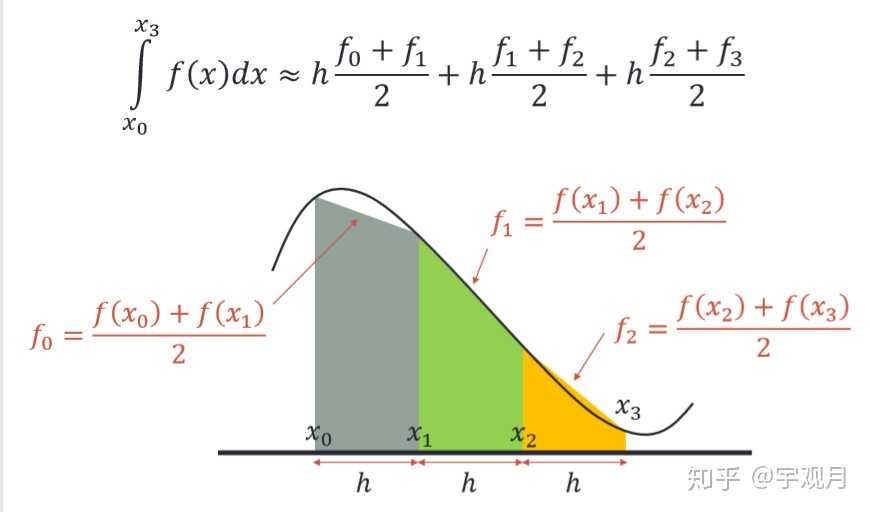
>> 2. 梯形法则
>> 3. 辛普森法则
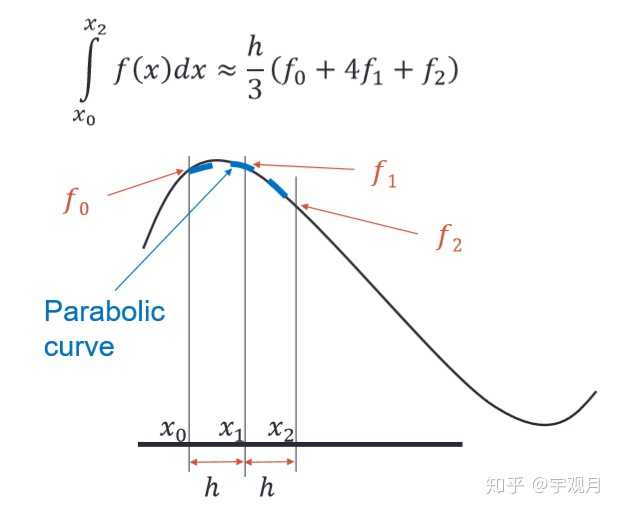
>> 三者之间的对比
4. 一重积分，二重积分及三重积分
>> 声明：
此笔记是通过观看台大郭彦甫老师的视频教程学习总结而来，想着边学习边记录，方便今后查阅。原视频教程见：
https://www.youtube.com/playlist?list=PLVHBjRDK0kALcQMwAFbR5q2driYZCHNIxwww.youtube.com
今天的文章贝塞尔函数积分用matlab_MATLAB 学习笔记-10微分与积分分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请发送邮件至 举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/29645.html
