经典排序算法（1）——冒泡排序算法详解

冒泡排序（Bubble Sort）是一种典型的交换排序算法，通过交换数据元素的位置进行排序。

一、算法基本思想

（1）基本思想

冒泡排序的基本思想就是：从无序序列头部开始，进行两两比较，根据大小交换位置，直到最后将最大（小）的数据元素交换到了无序队列的队尾，从而成为有序序列的一部分；下一次继续这个过程，直到所有数据元素都排好序。

算法的核心在于每次通过两两比较交换位置，选出剩余无序序列里最大（小）的数据元素放到队尾。

（2）运行过程

冒泡排序算法的运作如下：

1、比较相邻的元素。如果第一个比第二个大（小），就交换他们两个。

2、对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大（小）的数。

3、针对所有的元素重复以上的步骤，除了最后已经选出的元素（有序）。

4、持续每次对越来越少的元素（无序元素）重复上面的步骤，直到没有任何一对数字需要比较，则序列最终有序。

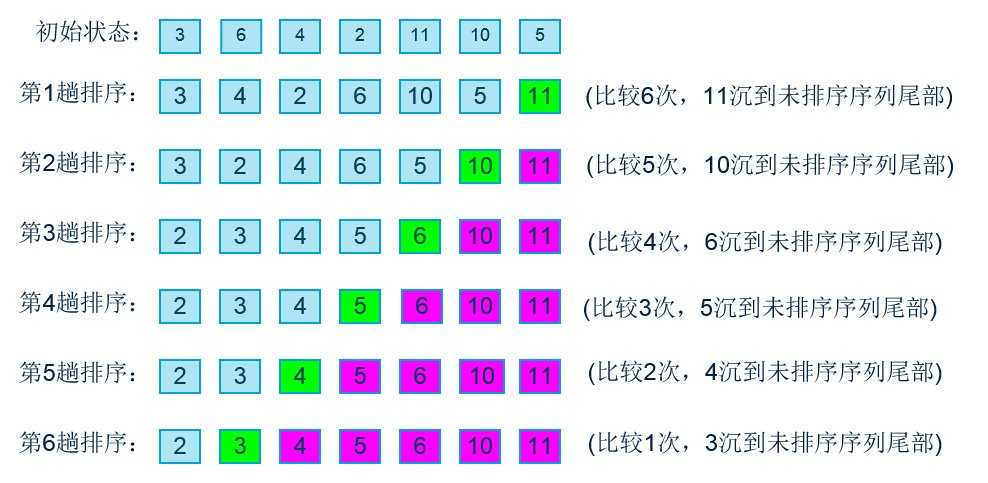
（3）示例

二、算法实现（核心代码）

C++实现：

void bubble_sort(int arr[], int len) {
	int i, j;
	for (i = 0; i < len - 1; i++)
		for (j = 0; j < len - 1 - i; j++)
			if (arr[j] > arr[j + 1])
				swap(arr[j], arr[j + 1]);
}

Java实现：

public static void bubble_sort(int[] arr) {
		int i, j, temp, len = arr.length;
		for (i = 0; i < len - 1; i++)
			for (j = 0; j < len - 1 - i; j++)
				if (arr[j] > arr[j + 1]) {
					temp = arr[j];
					arr[j] = arr[j + 1];
					arr[j + 1] = temp;
				}
}

三、算法改进和变种

（1）设置标志变量change

标志变量用于记录每趟冒泡排序是否发生数据元素位置交换。如果没有发生交换，说明序列已经有序了，不必继续进行下去了。

void bubble_sort(int arr[], int len) {
	int i, j, change=1;
        
	for (i = 0; i < len - 1 && change!=0; i++)
        {
                change=0;
		for (j = 0; j < len - 1 - i; j++)
			if (arr[j] > arr[j + 1])
                        {
				swap(arr[j], arr[j + 1]);
                                change = 1;
                         }
        }
}

（2）鸡尾酒排序

鸡尾酒排序又叫定向冒泡排序，搅拌排序、来回排序等，是冒泡排序的一种变形。此算法与冒泡排序的不同处在于排序时是以双向在序列中进行排序。

鸡尾酒排序在于排序过程是先从低到高，然后从高到低；而冒泡排序则仅从低到高去比较序列里的每个元素。它可以得到比冒泡排序稍微好一点的效能，原因是冒泡排序只从一个方向进行比对（由低到高），每次循环只移动一个项目。

以序列(2,3,4,5,1)为例，鸡尾酒排序只需要从低到高，然后从高到低就可以完成排序，但如果使用冒泡排序则需要四次。

但是在乱数序列的状态下，鸡尾酒排序与冒泡排序的效率都很差劲。

void cocktail_sort(int arr[], int len) {
	int j, left = 0, right = len - 1;
	while (left < right) {
		for (j = left; j < right; j++)
			if (arr[j] > arr[j + 1])
				swap(arr[j], arr[j + 1]);
		right--;
		for (j = right; j > left; j--)
			if (arr[j - 1] > arr[j])
				swap(arr[j - 1], arr[j]);
		left++;
	}
}

四、性能（算法时间、空间复杂度、稳定性）分析

（1）时间复杂度

在设置标志变量之后：

当原始序列“正序”排列时，冒泡排序总的比较次数为n-1，移动次数为0，也就是说冒泡排序在最好情况下的时间复杂度为O(n)；

当原始序列“逆序”排序时，冒泡排序总的比较次数为n(n-1)/2，移动次数为3n(n-1)/2次，所以冒泡排序在最坏情况下的时间复杂度为O(n^2)；

当原始序列杂乱无序时，冒泡排序的平均时间复杂度为O(n^2)。

（2）空间复杂度

冒泡排序排序过程中需要一个临时变量进行两两交换，所需要的额外空间为1，因此空间复杂度为O(1)。

（3）稳定性

冒泡排序在排序过程中，元素两两交换时，相同元素的前后顺序并没有改变，所以冒泡排序是一种稳定排序算法。