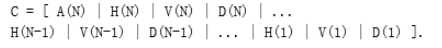小波指的是一种能量在时域非常集中的波，它的能量有限，都集中在某一点附近，而且积分的值为零，这说明它与傅里叶波一样是正交波。

图像的傅里叶变换是将图像信号分解为各种不同频率的正弦波。同样，小波变换是将图像信号分解为由原始小波位移和缩放之后的一组小波。小波在图像处理里被称为图像显微镜，原因在于它的多分辨率分解能力可以将图片信息一层一层分解剥离开来。剥离的手段就是通过低通和高通滤波器。

小波变换可以和傅里叶变换结合起来理解。傅里叶变换是用一系列不同频率的正余弦函数去分解原函数，变换后得到是原函数在正余弦不同频率下的系数。小波变换使用一系列的不同尺度的小波去分解原函数，变换后得到的是原函数在不同尺度小波下的系数。不同的小波通过平移与尺度变换分解，平移是为了得到原函数的时间特性，尺度变换是为了得到原函数的频率特性。

小波变换步骤：

1.把小波w(t)和原函数f(t)的开始部分进行比较，计算系数C。系数C表示该部分函数与小波的相似程度。

2.把小波向右移k单位，得到小波w(t-k)，重复1。重复该步骤直至函数f结束.

3.扩展小波w(t)，得到小波w(t/2)，重复步骤1,2.

4.不断扩展小波，重复1,2,3.

haar小波：

我这里使用的haar小波，缩放函数是[1 1]，小波函数是[1 -1]。是最简单的小波了。

图像二维离散小波变换：

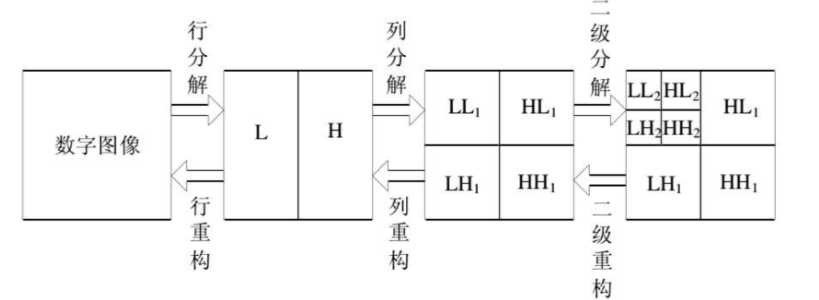
图像的二维离散小波分解和重构过程如下图所示，分解过程可描述为：首先对图像的每一行进行 1D-DWT，获得原始图像在水平方向上的低频分量 L 和高频分量 H，然后对变换所得数据的每一列进行 1D-DWT，获得原始图像在水平和垂直方向上的低频分量 LL、水平方向上的低频和垂直方向上的高频 LH、水平方向上的高频和垂直方向上的低频 HL 以及水平和垂直方向上的的高频分量 HH。

重构过程可描述为：首先对变换结果的每一列进行以为离散小波逆变换，再对变换所得数据的每一行进行一维离散小波逆变换，即可获得重构图像。由上述过程可以看出，图像的小波分解是一个将信号按照低频和有向高频进行分离的过程，分解过程中还可以根据需要对得到的 LL 分量进行进一步的小波分解，直至达到要求。

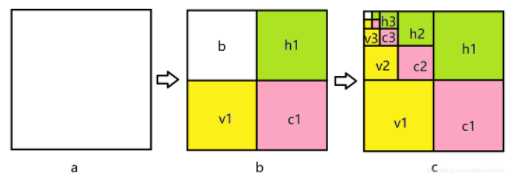
对于二维图像Haar变换不再从一个方向进行滤波，而是从水平和竖直两个方向进行低通和高通滤波（水平和竖直先后不影响），用图像表述如图所示：图中a表示原图，图b表示经过一级小波变换的结果，h1 表示水平反向的细节，v1 表示竖直方向的细节，c1表示对角线方向的细节，b表示下2采样的图像。图c中表示继续进行Haar小波变换。一级Haar小波变换实际效果如图3所示

matlab实例

小波去噪实现步骤：

（1）二维信号的小波分解。选择一个小波和小波分解的层次N，然后计算信号s到第N层的分解。
（2）对高频系数进行阈值量化。对于从1~N的每一层，选择一个阈值，并对这一层的高频系数进行软阈值量化处理。
（3）二维小波重构。根据小波分解的第N层的低频系数和经过修改的从第一层到第N的各层高频系数，计算二维信号的小波重构

Matlab函数介绍

1、dwt2是二维单尺度小波变换，其可以通过指定小波或者分解滤波器进行二维单尺度小波分解。DWT2的一种语法格式：[cA,cH,cV,cD]=dwt2(X,’wname’)；也就是说DWT2只能对某个输入矩阵X进行一次分解。

[cA1, cH1, cV1, cD1] = dwt2(I_noise, 'haar');
figure
subplot(221), imshow(cA1, []);
subplot(222), imshow(cH1, []);
subplot(223), imshow(cV1, []);
subplot(224), imshow(cD1, []);

可以看出，第一张图是图像的近似，相当于图像的低频部分，而其它三张图是图像的轮廓，也就是水平，垂直和对角三个方向的细节。是图像的高频部分。至此，各变量的维数如下所示。

2、wavedec2函数

该函数用于对多尺度二维小波进行分解，其常用调用格式：[C,S] = wavedec2(X,N,’wname’):

X：要进行小波分解的图像；
N ：指定分解的层数；
wname：指定用什么小波基进行分解。
输出：
c：为各层分解系数；
s: 各层分解系数长度，也就是大小。

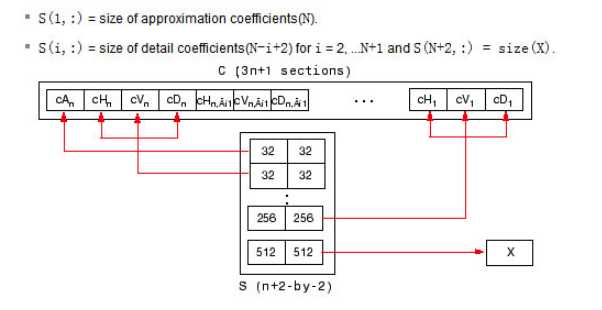
用小波函数wname对信号X在尺度N上的二维分解，其中N为大于1的正整数。可以对输入矩阵X进行N次分解。C代表分解系数的组合，是一个向量：

C的大小为 [1,img_height×img_width]；A(N)是图像第N层的近似表示，尺度最小，在金字塔中就是每层的下采样的图像，而H、V、D分别表示图像的水平高频分量，垂直高频分量，对角高频分量。正如我们在金字塔概念中所了解的，在第N-1层下采样到N层，N层的图像维度（尺度）是变小了，也就意味着在下采样过程中丢失了信息，而这些丢失的信息实质是高频信息，那么这些信息在小波分解中可以通过HVD这些高频分量来保存。
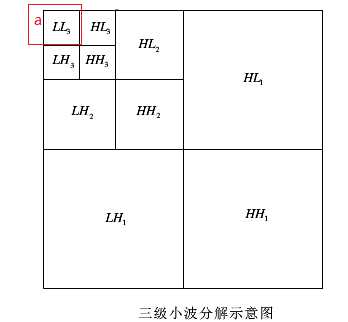
这里贴上小波分解之后的结果图，直观地感受一下。这里对原始图像进行三层小波分解。红框a表示的就是近似图像。

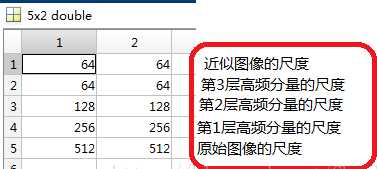
需要指出的是，每一次的小波分解都是在近似图像上进行分解。S 是储存各层分解系数长度的,即第一行是A(N)的长度,第二行是H(N)|V(N)|D(N)|的长度,第三行是 H(N-1)|V(N-1)|D(N-1)的长度,倒数第二行是H(1)|V(1)|D(1)长度,最后一行是原始图像img的长度(大小)。这里原始图像是512×512，并进行了3层的小波分解。对应的s内容如下图：

S表示每一层分解结果的维数，如果进行n层小波分解，S 的大小是(n+1)*2，最后一行表示的是原始图像的size。

3、wdcbm2函数

[thr,nkeep] = wdcbm2(c,s,alpha,m) 返回与level相关的阈值thr和要保持的系数数NKEEP，函数用于去噪或压缩。使用基于Birge-Massart策略的小波系数选择规则获得thr。通常，alpha= 1.5用于压缩，alpha= 3用于去噪。使用wdcbm2选择各层的独立阈值。

[C，S]是要由wavedec2函数得到的进行去噪或压缩的图像的小波分解结构，level j = size(S,1)-2.

THR是3*j的矩阵，THR（：，j）包含对于level j情况下，水平，对角线和垂直三个方向的阈值。 NKEEP是长度为j的向量，NKEEP（j）包含要保持在级别j情况下系数的数量。

j，M和ALPHA定义策略：

在j + 1级（和更粗略的级别），一切都保留。
对于从1到j的级别i，n_i最大系数保持为n_i = M /（j + 2-i）^ ALPHA。
M的默认值是M = prod（S（1，:)）最粗近似系数的数量。

4、wdencmp函数

[XC,CXC,LXC,PERF0,PERFL2] = wdencmp(‘lvd’,C,S,’wname’,N,THR,SORH)
函数wdencmp用于一维或二维信号的消噪或压缩。wname是所用的小波函数，gbl(global的缩写)表示每层都采用同一个阈值进行处理，lvd表示每层用不同的阈值进行处理，N表示小波分解的层数，THR为阈值3*N，SORH表示选择软阈值还是硬阈值(分别取为’s’和’h’)，XC是消噪或压缩后的信号，[CXC，LXC]是XC的小波分解结构，PERF0和PERFL2是恢复和压缩L^2的范数百分比, 是用百分制表明降噪或压缩所保留的能量成分。

5、wrcoef2函数

wrcoef2函数是用来重建一幅图像的系数，其实就是根据小波分解之后的系数c来重建其对应的图像。重建好的图像的尺度与原始图像一致。即无论你要重构哪个层的系数，最终它的维度都是和原始图像的尺度一致。其调用形式如下：
X = wrcoef2(‘type’,c,s,’wname’,N)

type ：指定要进行重构的小波系数，如a –近似图像 ;h – 水平高频分量;v – 垂直高频分量;d–对角高
频分量；
c: 是小波分解函数wavedec2分解的小波系数；
s: 是wavedec2分解形成的尺度；
wname ：指定小波基；
N ：指定重构的小波系数所在的层。默认重构最大层的系数，N = size(S,1)-2。N所指的层数是如何表示的？比如将图像小波分解成3层，那么N = 3是代表256×256那一层，还是64×64那一层？N=3 代表的是64×64那一层。

wrcoef2 的过程就相当于 appcoef2 或者 detcoef2 （抽取系数）后再进行 upcoef2（重构）。

clear;
close all;

file = 'lena_gray_512.tif';
img  = imread(file);
img = double(img);
% 对图像进行3层的小波分解
N = 3; % 设置分解层数
[c,s] = wavedec2(img,N,'db1');

% 对各层的近似图像a进行重构
a1 = wrcoef2('a',c,s,'db1',1);
a2 = wrcoef2('a',c,s,'db1',2);
a3 = wrcoef2('a',c,s,'db1',3);

6、appcoef2 函数

appcoef2适用于2维图像，其主要是为了提取小波分解中形成的近似图像，即低频分量。
A = appcoef2(c,s,’wname’,N)

c：小波分解的小波系数
s：小波分解的对应尺度
wname ：指定小波基
N ：指定小波系数所在的层数

7、detcoef2

函数detcoef2 用来对二维离散小波变换的高频部分系数进行提取。其调用形式为：
D = detcoef2(O,c,s,N)

O：指定提取哪个高频分量，取值分别为：’h’ –水平高频 or ‘v’ – 垂直高频 or ‘d’ – 对角高频；
c：小波系数矩阵；
s：尺度矩阵；

8、wthcoef2函数

该函数用于对二维信号的小波系数阈值进行处理，常用调用格式：
NC = wthcoef2(‘type’,C,S,N,T,SORH):返回经过小波分解结构[C,S]进行处理后的新的小波分解向量NC，[NC,S]即构成一个新的小波分解结构。N是一个包含高频尺度的向量，T是相应的阈值，且N和T长度须相等。返回’type’（水平、垂直、对角线）方向的小波分解向量NC。参数SORH用来对阈值方式进行选择，当SORH = ‘s’时，为软阈值，当SORH = ‘h’时，为硬阈值。

9、重构函数 waverec2

waverec2函数是wavedec2的反函数，返回的结果X就是原始图像。其基于小波分解结构[c,s]对矩阵X进行多级小波重构，其中[c,s]是wavedec2函数的返回值。其调用格式如下：
X = waverec2(c,s,’wname’) )