数据不平衡回归问题

问题提出

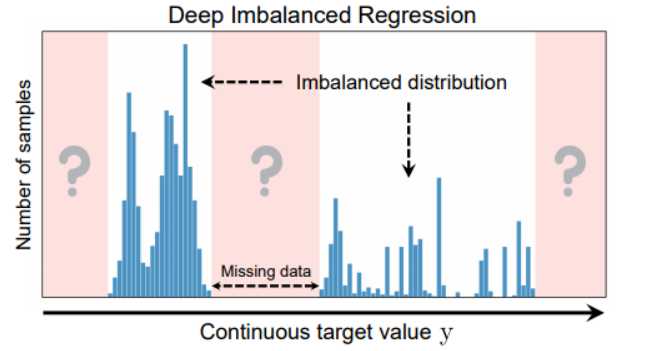
如上图，我们根据图像预测age，但age是一个连续值，并且中年时的样本多，老年和青年的样本少。如果将不同年龄划分为不同的类别来进行学习的话，是不太可能得到最佳的结果，因为这种方法没有利用到附近年龄人群之间特征的相似性。


数据不平衡回归问题基本状况如上图所示，1）样本分不均衡，2）目标值是连续的，3）甚至有的目标值范围内会缺失数据。

注意：如果训练阶段，部分目标值范围内数据缺失，而在测试时，该范围内又有数据，则模型推断（测试）时，会根据从训练数据学习到的知识进行推断，而模型从训练数据学习到的知识主体上是样本最多的目标范围内的数据知识。

标签分布平滑（LDS）

Label Distribution Smoothing

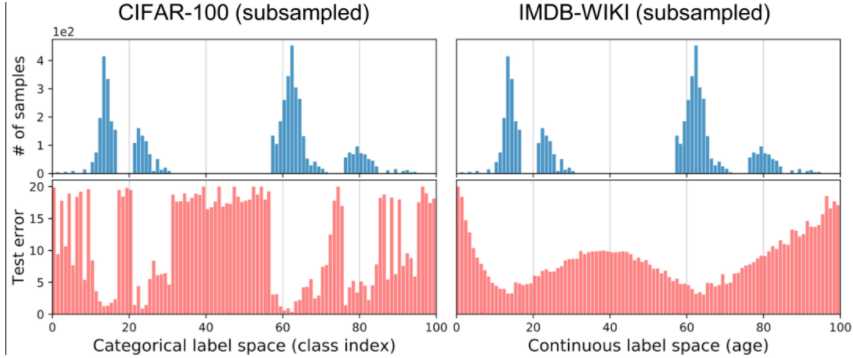
图上半部分是两个数据集采样构成的不平衡的标签分布，左部分的标签是离散的分类标签，右部分的标签值是连续的。图下半部分是训练相同模型进行预测的test error。可见数据多的error小，数据少的地方error大。另外：左边的标签密度分布与test error分布的皮尔森相关系数是 -0.76，右边为 -0.47。
可见，对于连续标签，标签数据分布与测试误差分布相关性小。所以我们要加入LDS：标签分布平滑来让它们的相关性大，进而使损失函数能更好的指导模型。

标签分布平滑：参考了在统计学习领域中的核密度估计，kernel density estimation的思路，来在这种情况下估计expected density。具体而言，给定连续的经验标签密度分布，LDS 使用了一个 symmetric kernel distribution 对称核函数，用经验密度分布与之进行卷积，来拿到一个 kernel-smoothed的版本，我们称之为 effective label density，也就是有效的标签密度，用来直观体现临近标签的数据样本具有的信息重叠的问题。那么我们也可以进一步验证，由LDS计算出的有效标签密度分布结果现已与误差分布良好相关，皮尔森相关系数为 −0.83。这表明了利用 LDS，我们能获得实际影响回归问题的不平衡的标签分布。

那么有了用LDS估计出的有效标签密度，之前用来解决类别不平衡问题的方法，便可以直接应用了。比如，对损失函数的重加权（re-weighting），或是直接修改损失函数，以及利用相关的特定学习技巧，例如 transfer learning，meta-learning，以及 two-stage training。

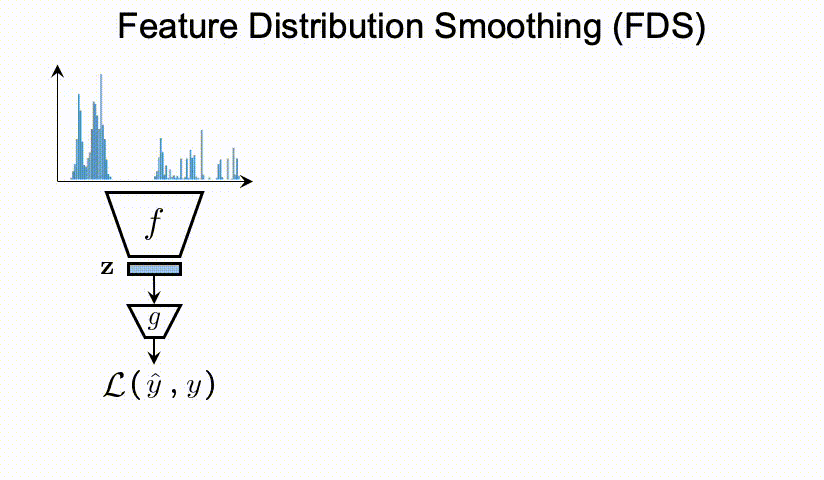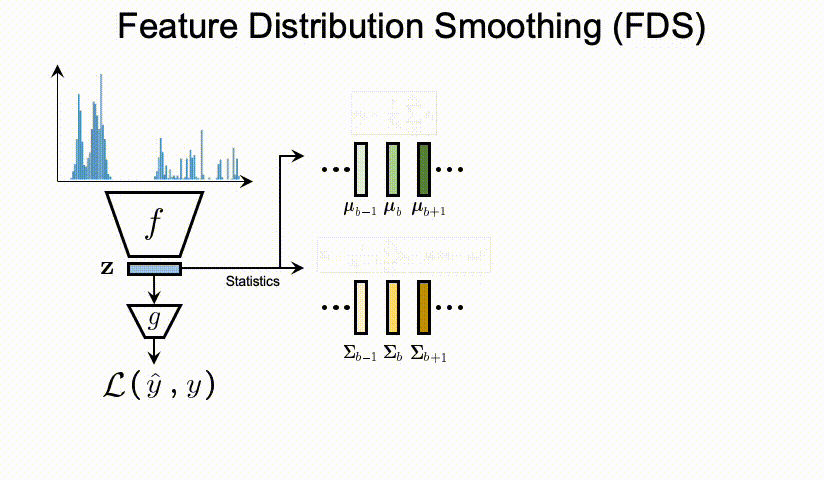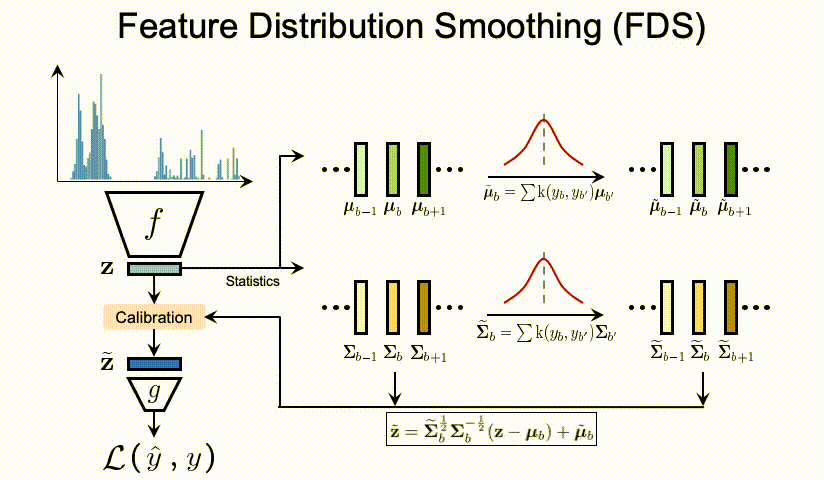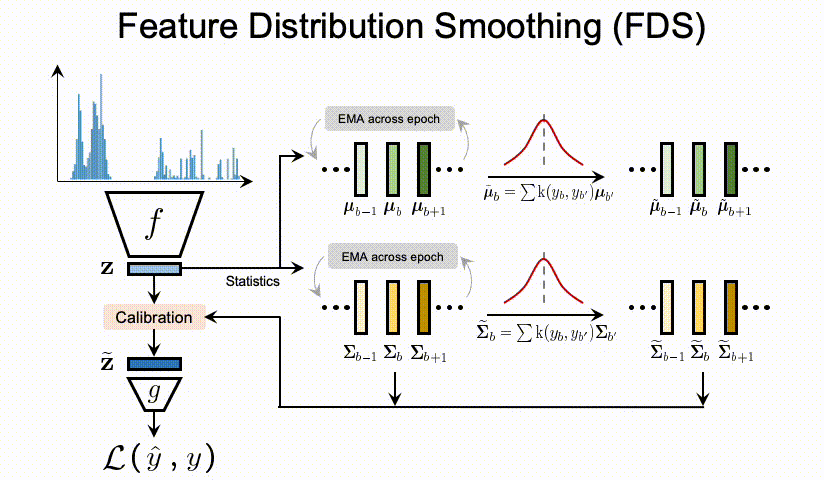
特征分布平滑（FDS）

该方法的主要思想是，相邻标签的数据特征应该是相似的，利用FDS可以把特征平滑到zero-shot的数据。这样会有提示并可以极大缓解《问题提出》中的注意。

过程：

利用估计的和平滑的统计量（$\mu 与\Sigma$），我们遵循标准的 whitening and re-coloring[10] 过程来校准每个输入样本的特征表示。那么整个FDS的过程可以通过在最终特征图之后插入一个特征的校准层(Calibration层)，来实现将FDS的集成到深度网络中。最后，我们在每个epoch 采用了对于 running statistics的 momentum update，也就是动量更新。这个是为了获得对训练过程中特征统计信息的一个更稳定和更准确的估计。
上图中计算${\mu }_{b-1}、{\mu }_b、{\mu }_{b+1}$与${\Sigma }_b...$用的是分箱操作。

那么就像之前提到的，FDS同样可以与任何神经网络模型以及之前类别不平衡的方法相集成。

引用

博客与论文：如何深入研究不平衡回归问题？

样本数量不均衡的损失函数

CB Loss：基于有效样本的类别不平衡损失

如图，和上一节问题一样，是针对多类别分类的问题。在图左，我们的样本较多，effective number的数目大，能更充实这个类别的语义空间。在图右，样本较少，effective number的数目小，在该类的语义空间中仍有大量的信息训练集中的样本不能覆盖到。另外，请注意上图中每个照片都有部分被覆盖，这代表每个照片发挥的作用不足1，很有可能只发挥了0.几。
图中的直线是做类别划分的超平面。黑色实线：直接在这些样本上训练的模型偏向于优势类。红色虚线：通过反向类频率来重新加权损失可能会在具有高类不平衡的真实数据上产生较差的性能。蓝虚线：设计了一个类平衡项，通过反向有效样本数来重新加权损失。

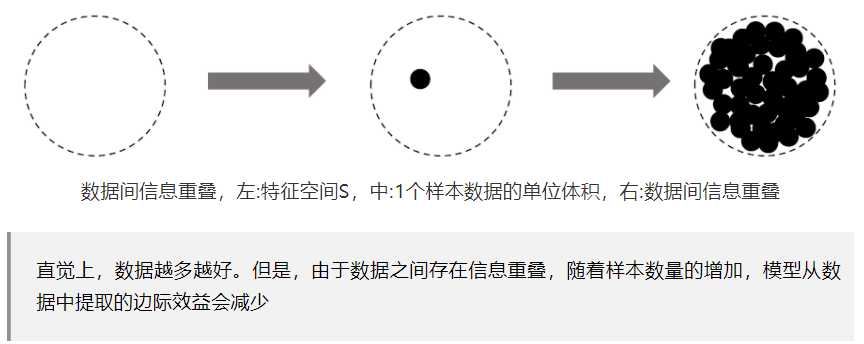
有效样本数量

左圆，设样本空间为N；中间圆，1个样本的期望样本体积为1；右圆，N个样本的期望体积比N小。

定义：将有效样本数定义为样本的期望体积。

结论：$期望体积E_n=\left(1-{\beta }^{\wedge }n\right)/(1-\beta )，其中\beta =(N-1)/N$。

归纳法证明：
设：一个新采样的数据点只能以两种方式与之前的采样数据交互：完全在之前的采样数据集中，概率为p，或完全在原来的数据集之外，的概率为1- p。

当采样第1个样本时，不存在重叠，$E_1=(1-{\beta }^1)/(1-\beta )=1$成立。
当采样第n个样本时，$$E_n=p{E}_{n-1}+(1-p)\left(E_{n-1}+1\right)=1+\frac{N-1}{N}{E}_{n-1}$$
此时，$$E_{n-1}=\left(1-{\beta }^{n-1}\right)/(1-\beta )$$
则，$$E_n=1+\beta \frac{1-{\beta }^{n-1}}{1-\beta }=\frac{1-\beta +\beta -{\beta }^n}{1-\beta }=\frac{1-{\beta }^n}{1-\beta }$$证毕。

损失函数的改写

模板：$$\mathrm{C}\mathrm{B}(\mathbf{p},y)=\frac{1}{E_{n_y}}\mathcal{L}(\mathbf{p},y)=\frac{1-\beta }{1-{\beta }^{n_y}}\mathcal{L}(\mathbf{p},y)$$其中，$\mathcal{L}(\mathbf{p},y)$为其他需要改写的损失函数。
$${\mathrm{C}\mathrm{B}}_{\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}}(\mathbf{z},y)=-\frac{1-\beta }{1-{\beta }^{n_y}}\log \left(\frac{\exp \left(z_y\right)}{{\sum }_{j=1}^C\exp \left(z_j\right)}\right)$$
$${\mathrm{C}\mathrm{B}}_{\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{m}\mathrm{o}\mathrm{i}\mathrm{d}}(\mathbf{z},y)=-\frac{1-\beta }{1-{\beta }^{n_y}}\sum _{i=1}^C\log \left(\frac{1}{1+\exp \left(-z_i^t\right)}\right)$$
$${\mathrm{C}\mathrm{B}}_{\text{focal }}(\mathbf{z},y)=-\frac{1-\beta }{1-{\beta }^{n_y}}\sum _{i=1}^C{\left(1-p_i^t\right)}^{\gamma }\log \left(p_i^t\right)$$

今天的文章深度学习里的长尾分布（类别样本不平衡）分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。