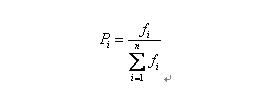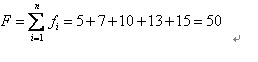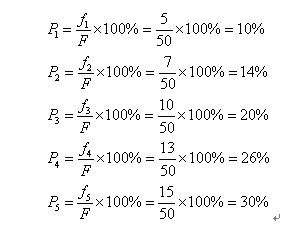一、遗传算法背景

    遗传算法的主要思想是借鉴于达尔文的自然选择下的进化论模型。通过借鉴生物进化论，遗传算法将要解决的问题模拟成一个生物进化的过程，通过复制、交叉、突变等操作产生下一代的解，并逐步淘汰掉适应度函数值低的解，增加适应度函数值高的解。这样进化N代后就很有可能会进化出适应度函数值很高的个体，也就是你的目标函数值的最优化结果。是时候展现真正的技术了：

    遗传算法中对目标的优化过程就好比生活中妹子在找男友时不断优化一样。假定影响妹子找男友的标准受两个变量的影响（也就是我们在优化时的自变量），此处假定为颜值和能力。最后对男生的综合评价（也就是适应度函数值）当然越高越好，于是乎在妹子一轮又一轮的筛选中（也就是遗传算法中的迭代过程）最后找到自己最满意的那位，但是记住，在这个过程中妹子可不会傻乎乎的减少自己的样本量，她会将评分低的个体淘汰后再引入新个体，这样才能保住自己最后找到的是最满意的！欲知妹子如何进行筛选，又如何引入新样本，请客官往下看：

二、遗传算法原理及其数学模型

    看了遗传算法的背景介绍发现好像也没多难，事实真的如此吗？对人而言，是乎很好理解，可问题是我们是在计算机上进行这个过程，该如何让计算机理解刚才的过程呢？
    假的在妹子心中对男友指标的方式为：
$$f(x,y)=sin(x)+cos(y)+0.1\ast x+0.1\ast y$$

2.1 编码方式

    首先，我们将计算机假定成生活里的妹子，现在她要开始找男朋友了！！！

    在该实例中，一个包含两条条染色体，分别为x，y。染色体上各自包含一组基因组。
    基因 ( Gene ) ：一个遗传因子。
    染色体 ( Chromosome ) ：一组的基因，有N个基因片段组成。
    个体 ( individual ) ：单个生物，由M条染色体构成。
    群体（population）：一群个体。
    在上述的例子中自变量有x，y。每个染色体由N个基因片段组成（由几个基因片段取决于你的编码精度），因此在本例子中：

    将染色体表达为基因的过程，称之为编码，常见的编码格式有二进制编码和浮点编码。

2.1.1 二进制编码

    二进制编码通俗的将就是将我们的自变量从十进制映射到N位的二进制，而N取决于我们要求的精度，例如求解精度为 e=0.02，那么我们需要将x的区间[-10 10]，切分成(10−(−10))/0.02=1000 份。
又因为采用二进制编码所以实际需要的编码位数为：
$$2^9=512<1000<2^{十}=1024$$
故当我们需要精度为0.02时，采用二进制编码最少需要10位数。那么实际的求解精度为：
$$e=20/1024\approx 0.01953$$
按照本文的例子，可以想到以下的映射,也就是对基因进行编码：

    同样，既然有编码，那一定就有解码：其实说白了就是把二进制数转换成十进制，然后在映射到自变量的取值范围内。我就知道你们特么绝对是一听就懂，一做就不会！

我知道，你们现在绝对流着口水等例子呢！

例子来了！！！
假如，现在某个染色体的基因为0101101011，那么它对应到自变量的取值空间（[-10 10]）的实数为
$$[0\ast 2^9+1\ast 2^8+0\ast 2^7+1\ast 2^6+1\ast 2^5+0\ast 2^4+1\ast 2^3+0\ast 2^2+1\ast 2^0]\ast (20/1024)-(-10)=17$$
懂了没！！！

至于如何生成10位的二进制数，当然是用matlab里面的rand命令了呀！！！生成一个1X10的矩阵就行了呀！！！

2.1.2 浮点数编码

    至于浮点型编码，其原理与二进制类似也是随机生成一个0到1之间的随机数，再映射到自变量取值空间，例如：0.3567对应的自变量实数为：
$$0.3567\ast [10-(-10)]-(10)=-2.866$$

2.2 种群初始化

    其实质就是生成一个初始化种群以供后面选择，就像一开始妹子随机选了100个男的当备胎，最后的最优个体从这里面不断优化得到！！！

2.3 计算初始种群的适应度函数值

    对生成的初始种群计算其个体的适应度值，这时种群中的个体就会因为适应度值大小不同而产生先后顺序，该过程可以理解为进化论物竞天择里的物竞过程，也就是自我竞争，至于天泽，卧槽，当然是妹子说了算啊，不一定你最牛皮人家就一定要你啊，这就好比有钱人不一定比穷人活的久啊，虽然大概率确实有钱人活的久，啊！万恶的金钱！！！可是我还是好想暴富！！！——真香！

2.4 对初始种群个体进行筛选—天泽（以轮盘赌方式进行选择）

    自然界中，越有钱的个体就越有可能活得久。但是也不能说钱越多的就肯定活的久，只能是从概率上来说更多。（毕竟有些人命是真的硬）。那么我们怎么来建立这种概率关系呢？下面我们介绍一种常用的选择方法――轮盘赌（Roulette Wheel Selection）选择法。假设种群数目,某个个体其适应度为,则其被选中的概率为：

比如我们有5条染色体，他们所对应的适应度评分分别为：5，7，10，13，15。
所以累计总适应度为：

所以各个个体被选中的概率分别为：

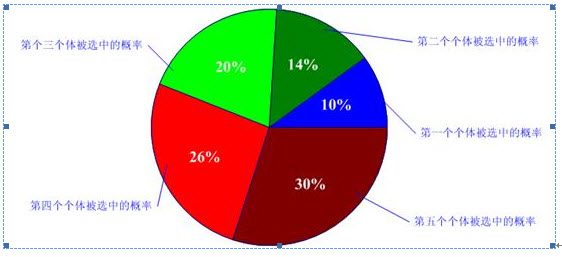
    呵呵，有人会问为什么我们把它叫成轮盘赌选择法啊？其实你只要看看下图的轮盘就会明白了。这个轮盘是按照各个个体的适应度比例进行分块的。你可以想象一下，我们转动轮盘，轮盘停下来的时候，指针会随机地指向某一个个体所代表的区域，那么非常幸运地，这个个体被选中了。（很明显，适应度评分越高的个体被选中的概率越大。）

所以说！！！有钱真的可以活的久！！！

2.5 个体染色体交叉及突变

    应该说这两个步骤就是使到子代不同于父代的根本原因（注意，不是优于哈！！！，只有经过自然的选择后，才会出现子代优于父代的倾向，这就好像博士父母的子女照样特么小学考试不及格一个道理！！！）。对于这两种遗传操作，二进制编码和浮点型编码在处理上有很大的差异，其中二进制编码的遗传操作过程，比较类似于自然界里面的过程，下面将分开讲述。
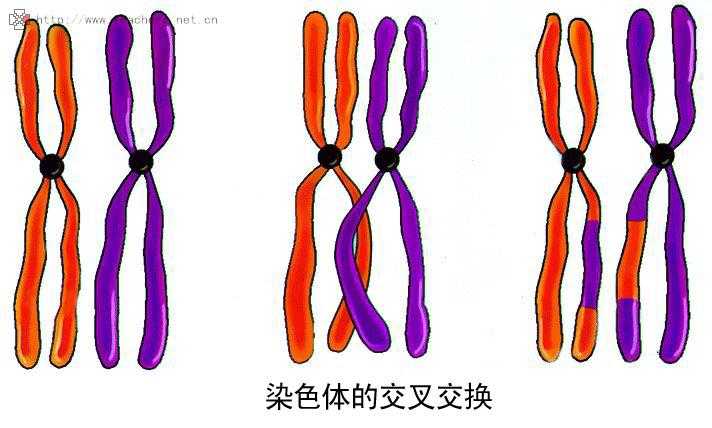
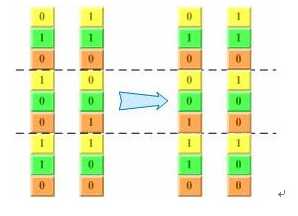
    从生物学中我们可以知道，染色体联会的过程中，分别来自父母双方之间的染色体常常发生交叉，并且相互交换一部分染色体，如图。事实上，二进制编码的基因交换过程也非常类似这个过程――随机把其中几个位于同一位置的编码进行交换，产生新的个体，如图所示。


    通过这两种处理，可以使被选择下来的个体产生新的变化，也就是产生新的变化！！！引入新变换来进行下一次自然选择！！！

2.6 精英选择及其作用

    精英选择的作用是保留每一次迭代过程中的最优个体，让其不再进行突变或者交叉变换，这样就会最大程度的保持最优解的继承性，而不会因为不断的交叉或者突变而导致最优解的结构被破坏，从而又产生一些没有意义的迭代！！！至于精英保留的个数，目前没有严格的理论支撑，我一般保留总群体的百分之十，也就是对前百分之十的个体进行直接保留！！！

三、遗传算法中关键参数的设定及作用

3.1 不同编码方式的区别及其作用

    根据个人经验哈（高手勿喷！），二进制编码进行优化的时候效果不明显，就是容易陷入局部最优化，因为二进制编码的话在进行交叉和突变后，把它反映到自变量实数空间后变化十分小，而不容易得到全局最优解！！！浮点型编码的话，进行交叉和突变处理后反映到自变量实数空间变化较大，于上一代有明显差异，更容易得到全局的最优解！！！

3.2 交叉算子与突变算子

    交叉算子与突变算子其实就是决定是否进行交叉变换和突变变换的阈值，在传统遗传算法中，这两个阈值在迭代过程中是定值，其实这样处理的效果不好，正确的是根据种群迭代的次数越来越多，也就是种群个体平均水平越来越好之后，交叉和突变越不容易进行，就好比，一个代码，刚开始的时候很不完善，易于修改（看成突变和交叉），但是到后面不断优化以后，代码越来越完善之后，越来越不容易修改了（突变和交叉），所以在改进遗传算法中，应该引入自适应交叉和突变算子，让其随着迭代次数的增加而降低！！！至于按什么规律降，，，，，，，，，这么简单的问题！！！，，，，，，，,，，我也不会啊！！！看论文吧

3.3 精英数量

    说实话，这玩意儿和交叉、突变算子变化刚好相反，这个是在前期保留的少，后期应该加多，毕竟到后期大家都牛皮的的嘛！！！至于按什么规律保留，，，，我还是不知道！！！随缘，多试几次，哪个效果好要哪个！！！

四、遗传算法matlab实现代码

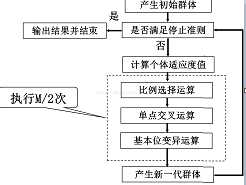
    可以，又到了大家期待的代码展示环节（别跟我说什么原理，数学公式，没代码的讲解都是扯淡！！！）下面我们将按照遗传算法的流程图顺序相应给出代码，为了便于理解，我们先给出主程序，再分别给出子程序：

4.1 主程序

clc;
clear;
%% 基础参数
N = 100;  %种群内个体数目
N_chrom = 2; %染色体节点数，也就是每个个体有多少条染色体，其实说白了就是看适应函数里有几个自变量。
iter = 1000; %迭代次数，也就是一共有多少代
mut = 0.2;  %突变概率
acr = 0.2; %交叉概率
best = 1;
chrom_range = [-10 -10;10 10];%每个节点的值的区间
chrom = zeros(N, N_chrom);%存放染色体的矩阵
fitness = zeros(N, 1);%存放染色体的适应度
fitness_ave = zeros(1, iter);%存放每一代的平均适应度
fitness_best = zeros(1, iter);%存放每一代的最优适应度
chrom_best = zeros(1, N_chrom+1);%存放当前代的最优染色体与适应度
%% 初始化，这只是用于生成第一代个体，并计算其适应度函数
chrom = Initialize(N, N_chrom, chrom_range); %初始化染色体
fitness = CalFitness(chrom, N, N_chrom); %计算适应度
chrom_best = FindBest(chrom, fitness, N_chrom); %寻找最优染色体
fitness_best(1) = chrom_best(end); %将当前最优存入矩阵当中
fitness_ave(1) = CalAveFitness(fitness); %将当前平均适应度存入矩阵当中
%% 用于生成以下其余各代，一共迭代多少步就一共有多少代
for t = 2:iter
    chrom = MutChrom(chrom, mut, N, N_chrom, chrom_range, t, iter); %变异
    chrom = AcrChrom(chrom, acr, N, N_chrom); %交叉
    fitness = CalFitness(chrom, N, N_chrom); %计算适应度
    chrom_best_temp = FindBest(chrom, fitness, N_chrom); %寻找最优染色体
    if chrom_best_temp(end)>chrom_best(end) %替换掉当前储存的最优
        chrom_best = chrom_best_temp;
    end
    %%替换掉最劣
    [chrom, fitness] = ReplaceWorse(chrom, chrom_best, fitness);
    fitness_best(t) = chrom_best(end); %将当前最优存入矩阵当中
    fitness_ave(t) = CalAveFitness(fitness); %将当前平均适应度存入矩阵当中
end
%% 作图
figure(1)
plot(1:iter, fitness_ave, 'r', 1:iter, fitness_best, 'b')
grid on
legend('平均适应度', '最优适应度')
e=PlotModel(chrom_best);
%% 输出结果
disp(['最优染色体为', num2str(chrom_best(1:end-1))])
disp(['最优适应度为', num2str(chrom_best(end))])

4.2 种群初始化

function chrom_new = Initialize(N, N_chrom, chrom_range)
chrom_new = rand(N, N_chrom);
for i = 1:N_chrom %每一列乘上范围
    chrom_new(:, i) = chrom_new(:, i)*(chrom_range(2, i)-chrom_range(1, i))+chrom_range(1, i);
end

4.3 适应度计算

function fitness = CalFitness(chrom, N, N_chrom)
fitness = zeros(N, 1);
%开始计算适应度
for i = 1:N
    x = chrom(i, 1);
    y = chrom(i, 2);
    fitness(i) = sin(x)+cos(y)+0.1*x+0.1*y;%%该函数是定义的适应度函数，也可称为代价函数，用于以后筛选个体的评价指标
end

4.4 选择淘汰

function chrom_best = FindBest(chrom, fitness, N_chrom)
chrom_best = zeros(1, N_chrom+1);
[maxNum, maxCorr] = max(fitness);%因为所有个体对应的适应度大小都被存放在fitness矩阵中
chrom_best(1:N_chrom) =chrom(maxCorr, :);
chrom_best(end) = maxNum;

4.5 变异处理

%% 用于对每代共100个个体进行变异处理
function chrom_new = MutChrom(chrom, mut, N, N_chrom, chrom_range, t, iter)
for i = 1:N %%N是个体总数，也就是每一代有多少头袋鼠
    for j = 1:N_chrom  %N_chrom是染色体节点数，就是有几条染色体
        mut_rand = rand; %随机生成一个数，代表自然里的基因突变，然后用改值来决定是否产生突变。
        if mut_rand <=mut  %mut代表突变概率，即产生突变的阈值，如果小于0.2的基因突变概率阈值才进行基因突变处理，否者不进行突变处理
            mut_pm = rand; %增加还是减少
            mut_num = rand*(1-t/iter)^2;
            if mut_pm<=0.5
                chrom(i, j)= chrom(i, j)*(1-mut_num);
            else
                chrom(i, j)= chrom(i, j)*(1+mut_num);
            end
            chrom(i, j) = IfOut(chrom(i, j), chrom_range(:, j)); %检验是否越界
        end
    end
end
chrom_new = chrom;%%把变异处理完后的结果存在新矩阵里

4.6 变异是否超出自变量范围判断

function c_new = IfOut(c, range)
if c<range(1) || c>range(2)
    if abs(c-range(1))<abs(c-range(2))
        c_new = range(1);
    else
        c_new = range(2);
    end
else
    c_new = c;
end

4.7 交叉处理

function chrom_new = AcrChrom(chrom, acr, N, N_chrom)
for i = 1:N
    acr_rand = rand;%生成一个代表该个体是否产生交叉的概率大小，用于判别是否进行交叉处理
    if acr_rand<acr %如果该个体的交叉概率值大于产生交叉处理的阈值，则对该个体的染色体（两条，因为此案例中有两个自变量）进行交叉处理
        acr_chrom = floor((N-1)*rand+1); %要交叉的染色体
        acr_node = floor((N_chrom-1)*rand+1); %要交叉的节点
        %交叉开始
        temp = chrom(i, acr_node);
        chrom(i, acr_node) = chrom(acr_chrom, acr_node); 
        chrom(acr_chrom, acr_node) = temp;
    end
end
chrom_new = chrom;

4.8 最差个体统计

function [chrom_new, fitness_new] = ReplaceWorse(chrom, chrom_best, fitness)

max_num = max(fitness);
min_num = min(fitness);
limit = (max_num-min_num)*0.2+min_num;

replace_corr = fitness<limit;

replace_num = sum(replace_corr);
chrom(replace_corr, :) = ones(replace_num, 1)*chrom_best(1:end-1);
fitness(replace_corr) = ones(replace_num, 1)*chrom_best(end);
chrom_new = chrom;
fitness_new = fitness;

end

4.9 计算平均适应度值

function fitness_ave = CalAveFitness(fitness)
[N ,~] = size(fitness);
fitness_ave = sum(fitness)/N;

4.10 绘制结果

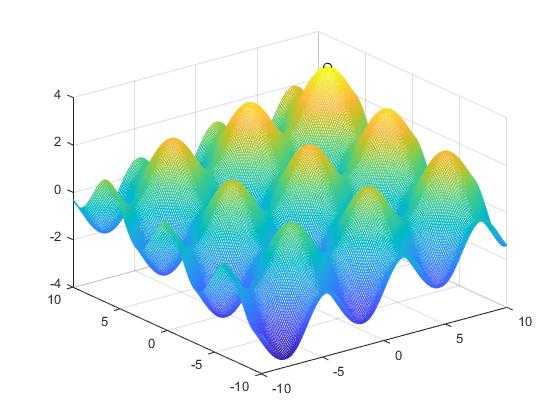
function y = PlotModel(chrom)
x = chrom(1);
y = chrom(2);
z = chrom(3);
figure(2)
scatter3(x, y, z, 'ko')
hold on
[X, Y] = meshgrid(-10:0.1:10);
Z =sin(X)+cos(Y)+0.1*X+0.1*Y;
mesh(X, Y, Z)
y=1;

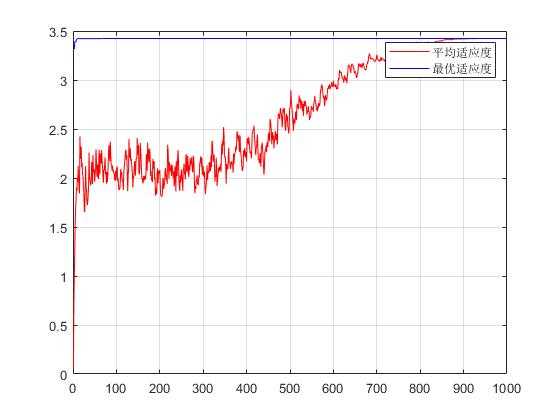
4.11 仿真效果如下：

5 结尾篇

用心花时间写了这么多，这么久！！！懂我的意思吧！！！


[1]: https://blog.csdn.net/emiyasstar__/article/details/6938608/
[2]: https://blog.csdn.net/xuehuafeiwu123/article/details/52327559
[3]: https://blog.csdn.net/tsroad/article/details/52464108
[4]: https://blog.csdn.net/emiyasstar__/article/details/6938608/

今天的文章遗传算法原理及其matlab程序实现分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。