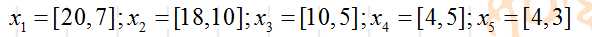聚类分析的Matlab 程序—系统聚类

(1)计算数据集每对元素之间的距离,对应函数为pdistw.

调用格式：Y=pdist(X),Y=pdist(X,’metric’), Y=pdist(X,’distfun’),Y=pdist(X,’minkowski’,p)

说明：X是m*n的矩阵，metric是计算距离的方法选项：

metric=euclidean表示欧式距离（缺省值）；

metric=seuclidean表示标准的欧式距离；

metric=mahalanobis表示马氏距离。

distfun是自定义的距离函数，p是minkowski距离计算过程中的幂次，缺省值为2.Y返回大小为m(m-1)/2的距离矩阵，距离排序顺序为(1,2),(1,3),…(m-1,m)，Y也称为相似矩阵，可用squareform将其转化为方阵。

（2）对元素进行分类，构成一个系统聚类树，对应函数为linkage.

调用格式：Z=linkage(Y), Z=linkage(Y,’method’)

说明：Y是距离函数，Z是返回系统聚类树，method是采用的算法选项，

如下：method=single表示最短距离(缺省值)；

complete表示最长距离；median表示中间距离法；

centroid表示重心法；average表示类平均法；

ward 表示离差平方和法（Ward法）。

（3）确定怎样划分系统聚类树，得到不同的类，对应的函数为cluster.

调用格式：T=cluster(Z,’cutoff’,c),T=cluster(Z,’maxclust’,n)

说明：Z是系统聚类树，为(m-1)*3的矩阵，c是阈值，n是类的最大数目，

maxclust是聚类的选项，cutoff是临界值，决定cluster函数怎样聚类。

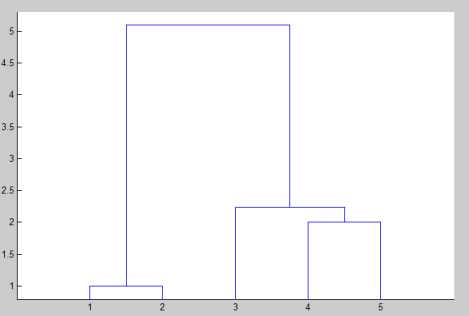
例题1 利用系统聚类法对5个变量进行分类。

matlab程序

%Matlab运行程序：
X=[20,7;18,10;10,5;4,5;4,3];
Y=pdist(X);
SF=squareform(Y);
Z=linkage(Y，’single’);
dendrogram(Z);%显示系统聚类树
T=cluster(Z,'maxclust',3)

例题2

%例2的程序设计：
X=[1 1;1 2;6 3;8 2;8 0];
Y=pdist(X);
SF=squareform(Y);
Z=linkage(Y,'single');
dendrogram(Z)；
T=cluster(Z,'maxclust',3)

聚类分析案例

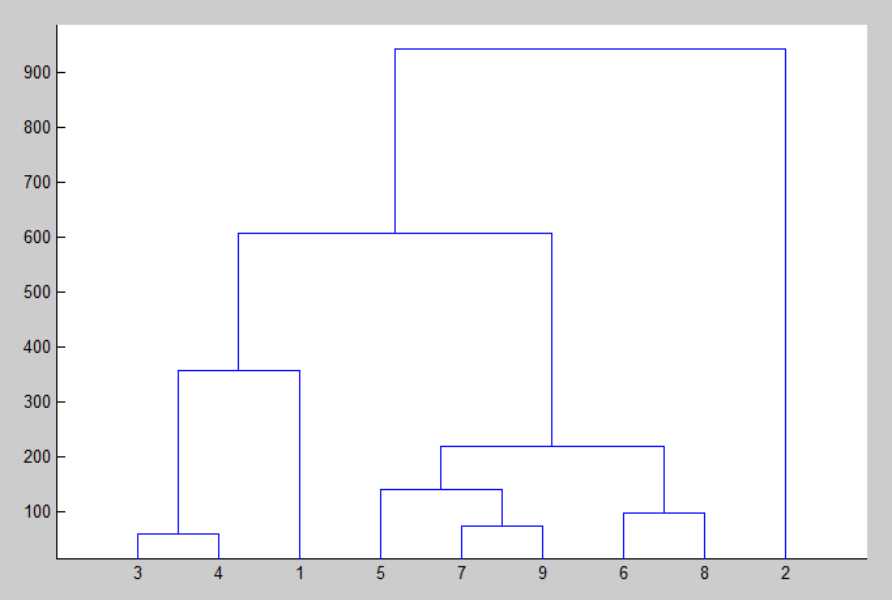
    根据第三产业国内生产总值的9 项指标，对华东地区6 省1 市进行分类，原始数据如下表：

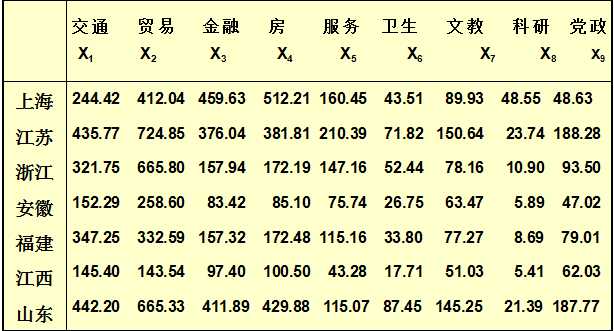
%Matlab程序如下：
X=[244.42    412.04   459.63    512.21  160.45    43.51     89.93    48.55   48.63
435.77    724.85   376.04    381.81  210.39    71.82   150.64     23.74  188.28
321.75    665.80   157.94    172.19  147.16    52.44     78.16     10.90    93.50                                                                       
152.29    258.60     83.42      85.10    75.74    26.75     63.47       5.89    47.02                                                                
347.25    332.59   157.32    172.48  115.16    33.80     77.27       8.69    79.01                                                                    
145.40    143.54     97.40    100.50    43.28    17.71     51.03       5.41    62.03                                                                  
442.20    665.33    411.89   429.88   115.07   87.45   145.25     21.39  187.77 ]';
Y=pdist(X);
SF=squareform(Y);
Z=linkage(Y,'average');
dendrogram(Z);
T=cluster(Z,'maxclust',3)

今天的文章聚类分析的Matlab 程序—系统聚类（附有案例分析）分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。