使用python实现智能浇筑方案

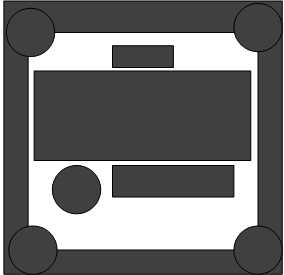
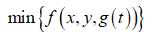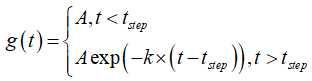具体方案如下所示：

根据这个地图，我们构建1010矩阵，大概草图如下所示：

然后，根据之前的设计要求，我们假设浇筑满的时间为t1~tN。

然后浇筑的速度随着时间的变换而逐渐变小，假设其流速的函数为

然后是浇筑的位置假设为(x，y)

那么，实际浇筑的问题，可以转换为如下的数学模型：

即，通过优化选择最优的位置x和y，以及控制胶水浇筑的流速，使得填满整个白色区域的时间最小，且不溢出。

根据这些信息，我们构建如下的具体模型：

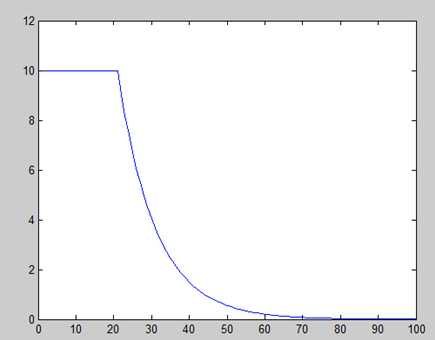
未知变量有A，即图中10，

tstep，图中为20

缓慢降低指数，k，图中为0.1.

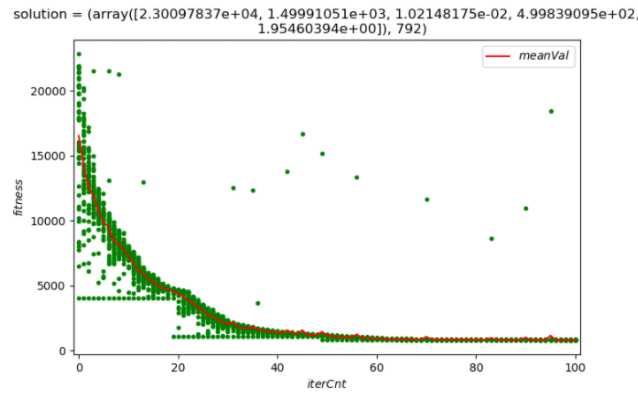
先运行main.py，这个是上述优化算法的优化过程，因为图片上可以优化的情况又数百万种情况，所以仿真速度较慢，大概1个小时后，会得到如下结果：

运行后，得到参数

以及浇筑位置：

得到实际的浇筑效果

达到了预期的效果，即一开始较快，然后在到细通道的时候，逐渐变慢。

部分python代码如下所示：

import numpy
import matplotlib.pyplot as plt
import math
import random
import matplotlib.pyplot as plt
import matplotlib.image as mpimg # mpimg 用于读取图片
import cv2
import numpy as np
from utiles import *
from PIL import Image

global h
global obstacles
global S
global h
global Xcan
global Ycan
global row
global col

# 目标函数2
# def bestAB_models(x1, x2, x3, x4, x5):
#     return abs(x1+x2+x3+x4+x5)

def bestAB_models(x1, x2, x3, x4, x5):
    idx   = math.floor(x1);

    x     = round(Xcan[idx]);
    y     = round(Ycan[idx]);
    A     = x2;
    k     = x3;
    tstep = x4;
    B     = x5;
    Times = 1000;
    g = np.zeros((1, Times));
    for i in range(0, Times):
        if i <= tstep:
            g[0, i] = A
        if i > tstep:
            g[0, i] = (A – B) * np.exp(-1 * k * (i – tstep)) + B;

    S0 = h * S;
    rest = 1;
    tt = 0;
    ks = 0.0005/50;
    V = 0;
    flag = np.zeros((1,40000));
    while (rest>0):
        tt=tt+1
        W, L = funcW(obstacles, x, y, row, col)
        if tt<=Times:
           gt=g[0, tt-1];
        else:
           gt=40;
        HS = gt * ks / min(W, L);

        if (HS>h) | (W<90|L<20):#溢出
           flag[0,tt-1] = 1;
        else:
           flag[0,tt-1] = 0;
        S0 = S0 – gt;
        rest = S0;

    if (sum(sum(flag))>0):
        tt=10000000000

    return tt

# 遗传算法: 选择, 交叉, 变异
class GA(object):

    def __init__(self, func, lbounds, ubounds, population_size=100, maxIter=500, pm=0.001, speed=3, cf=0.999):
        self.func = func  # 目标函数
        self.lbounds = lbounds  # 搜寻下界
        self.ubounds = ubounds  # 搜寻上界
        self.population_size = population_size  # 种群规模
        self.maxIter = maxIter  # 最大迭代次数
        self.pm = pm  # 变异概率(0, 1)
        self.speed = speed  # 种群收敛速度[1, +∞)
        self.cf = cf  # 交叉因子(0, 1)

        self.size = len(lbounds)  # 搜索空间的维度
        self.best_chrom_fitness = list()  # 最优染色体(染色体, 适应度)迭代记录列表
        self.__record_fitness = list()  # 种群适应度迭代记录列表

    def solve(self):
        # 种群随机初始化
        population = self.__init_population()
        # 记录种群最优染色体信息
        self.__add_best(population)

        for i in range(self.maxIter):
            print(i)
            # 种群更新
            population = self.__selection(population)
            population = self.__crossover(population)
            population = self.__mutation(population)

            # 上一代最优个体无条件保留至下一代
            population[0] = self.best_chrom_fitness[-1][0]
            # 记录种群最优个体
            self.__add_best(population)

        self.solution = self.best_chrom_fitness[-1]

    # 选择: 轮盘赌方法
    def __selection(self, population):
        # 适应度排序
        fitness = self.__cal_fitness(population)
        new_fitness = sorted(list((ele, idx) for idx, ele in enumerate(fitness)), key=lambda item: item[0],
                             reverse=True)
        # 轮盘区间计算 -> 采用多项式函数对收敛速度进行调整
        roulette_interval = self.__cal_interval()
        # 随机飞镖排序
        random_dart = sorted(numpy.random.random(self.population_size))

        new_population = list()
        idx_interval = idx_dart = 0
        while idx_dart < self.population_size:
            if random_dart[idx_dart] > roulette_interval[idx_interval]:
                idx_interval += 1
            else:
                new_population.append(population[new_fitness[idx_interval][1]])
                idx_dart += 1

        # 顺序打乱
        numpy.random.shuffle(new_population)
        return new_population

    # 交叉: 对称凸组合
    def __crossover(self, population):
        # 交叉随机数 -> 采用交叉因子提高计算精度
        alpha = numpy.random.random(self.population_size – 1) * self.cf

        for idx in range(self.population_size – 1):
            new_chrom1 = alpha[idx] * population[idx] + (1 – alpha[idx]) * population[idx + 1]
            new_chrom2 = alpha[idx] * population[idx + 1] + (1 – alpha[idx]) * population[idx]
            population[idx] = new_chrom1
            population[idx + 1] = new_chrom2

        return population

    # 变异: 全空间变异
    def __mutation(self, population):
        # 变异概率随机数
        mutation_prob = numpy.random.random(self.population_size)

        for idx, prob in enumerate(mutation_prob):
            if prob <= self.pm:
                # 变异幅度随机数
                mutation_amplitude = numpy.random.uniform(-1, 1, self.size)
                for idx_dim, ampli in enumerate(mutation_amplitude):
                    if ampli >= 0:  # 正向变异
                        population[idx][idx_dim] += ampli * (self.ubounds[idx_dim] – population[idx][idx_dim])
                    else:  # 负向变异
                        population[idx][idx_dim] += ampli * (population[idx][idx_dim] – self.lbounds[idx_dim])

        return population

    # 种群随机初始化
    def __init_population(self):
        population = list()

        for i in range(self.population_size):
            chrom = list()
            for j in range(self.size):
                chrom.append(numpy.random.uniform(self.lbounds[j], self.ubounds[j]))
            population.append(numpy.array(chrom))

        return population

    # 种群适应度计算
    def __cal_fitness(self, population):
        fitness = list(self.func(*chrom) for chrom in population)
        return fitness

    # 记录种群最优染色体信息
    def __add_best(self, population):
        fitness = self.__cal_fitness(population)
        self.__record_fitness.append(fitness)
        min_idx = numpy.argmin(fitness)
        self.best_chrom_fitness.append((population[min_idx], fitness[min_idx]))

    # 轮盘区间计算
    def __cal_interval(self, speed=2):
        tmp = (numpy.arange(self.population_size) + 1) / self.population_size
        tmp_normalize = tmp / (self.population_size + 1) * 2

        roulette_interval = list()
        curr_sum = 0
        for item in tmp_normalize:
            curr_sum += item
            roulette_interval.append(curr_sum)

        roulette_interval = numpy.array(roulette_interval) ** self.speed
        return roulette_interval

    # 求解过程可视化展示
    def display(self):
        fig = plt.figure(figsize=(8, 5))
        axes = plt.subplot()
        axes.plot(self.__record_fitness, ‘g.’)
        axes.plot(numpy.array(self.__record_fitness).sum(axis=1) / self.population_size, ‘r-‘, label=’$meanVal$’)
        axes.set(xlim=(-1, self.maxIter + 1), xlabel=’$iterCnt$’, ylabel=’$fitness$’)
        axes.set(title=’solution = {}’.format(self.solution))
        axes.legend()
        fig.savefig(‘myGA.png’, dpi=500)
        plt.show()
        plt.close()

if __name__ == ‘__main__’:
     #读取地图，读取地图的参数信息
     map = mpimg.imread(‘map.jpg’)
     obstacles = cv2.cvtColor(map, cv2.COLOR_BGR2GRAY)
     obstacles2 = obstacles;
     h = 30;#假设高度
     map.shape
     row = map.shape[0]
     col = map.shape[1]
     KK = map.shape[2]
     #计算空白区域面积
     S  = 0;
     for i in range(0, row):  # 遍历所有长度的点
         for j in range(0, col):  # 遍历所有宽度的点
             if obstacles2[i, j] > 100:
                 obstacles[i, j] = 1
                 S = S+1;
             else:
                 obstacles[i, j] = 0

     Xcan, Ycan = findm(obstacles, row, col)

     # x = round(Xcan[idx]);
     # y = round(Ycan[idx]);
     # A = x2;
     # k = x3;
     # tstep = x4;
     # B = x5;

     #五个参数含义，第一个就是浇筑大概范围，别太大，否则搜索会错误，第二个到第五个就是我g里面的四个参数
     ins = GA(bestAB_models, [23000, 100,0.01,1,0], [23600, 1500,0.05,500,50], population_size=50, maxIter=100, pm=0.005, speed=1, cf=0.95)
     ins.solve();
     ins.display();

A43-006

今天的文章使用python实现智能浇筑方案分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。