本人目前大数据专业大二在读，获得过全国大学生数学建模竞赛一等奖，喜欢研究人工智能。有很多同学询问我数模是怎么学的，参考了哪些教材。其实我基本都是研究一些论文、博客之类的，也很难推荐。所以我开了个这个专栏，之后有空的话可能会上传一些我整理的数学模型，感兴趣的同学可以看看🌹。

前言

本文主要介绍了线性模型在数学建模中的应用，以及python的实现，旨在帮助同学们了解如何建立一个线性模型。文章主要针对初学者，所以写了一些基础知识，大佬可以略过。
线性模型就像万金油一样，虽然很基础、很简单，但是真的真的很好用！所以我决定从这个基础模型开始向大家展示数学建模的魅力！

线性模型概述

简介

线性模型是在实践中广泛使用的一类模型，几十年来被广泛研究，它可以追溯到一百多年前。线性模型利用数据特征的线性函数(linear function)，对输入数据进行拟合，得到结果。虽然线性模型只是根据线性关系对数据进行拟合，但它在分类与回归问题中均适用，使用范围较广。

🔔监督机器学习问题主要有两种，分别叫作分类(classifification)与回归(regression)。
分类问题的目标是预测类别标签(class label)，这些标签来自预定义的可选列表。分类问题有时可分为二分类(binary classifification，在两个类别之间进行区分的一种特殊情况)和多分类(multiclass classifification，在两个以上的类别之间进行区分)。
回归任务的目标是预测一个连续值，编程术语叫作浮点数(flfloating-point number)，数学术语叫作实数(real number)。根据教育水平、年龄和居住地来预测一个人的年收入，这就是回归的一个例子。

作用

在数学建模中，线性模型主要有以下两个作用：

1. 对结果进行预测。这个应该比较好理解，比如预测房价数据等。
2. 分析自变量对因变量的影响大小。一般题目会问：各因素对某一个数据（如房价）的影响大小之类的，后面还会介绍。

用于回归的线性模型

模型

对于回归问题，一般会建立如下模型：
$$y^{\ast }=w_0\ast x_0+w_1\ast x_1+...+w_n\ast x_n+b$$
其中，xi(i=1,2…n)为各特征，wi(i=1,2…n)为各特征权重(即要计算的参数)，y*为模型的预测结果。
对于只有一个特征的数据，模型如下：
$$y^{\ast }=w_0\ast x_0+b$$
你可能还记得，这就是高中数学里的直线方程。这里 w[0] 是斜率，b 是 y 轴截距。对于有更多特征的数据集，w 包含沿每个特征坐标轴的斜率。或者，你也可以将预测的值看作输入特征的加权求和，权重由 w 的元素给出(可以取负值)。

🔔因此根据权重w可以反映出各特征对y的影响大小。且权重越大，影响越大。如果只是分析特征影响大小的话，就不需要在意截距b的大小。

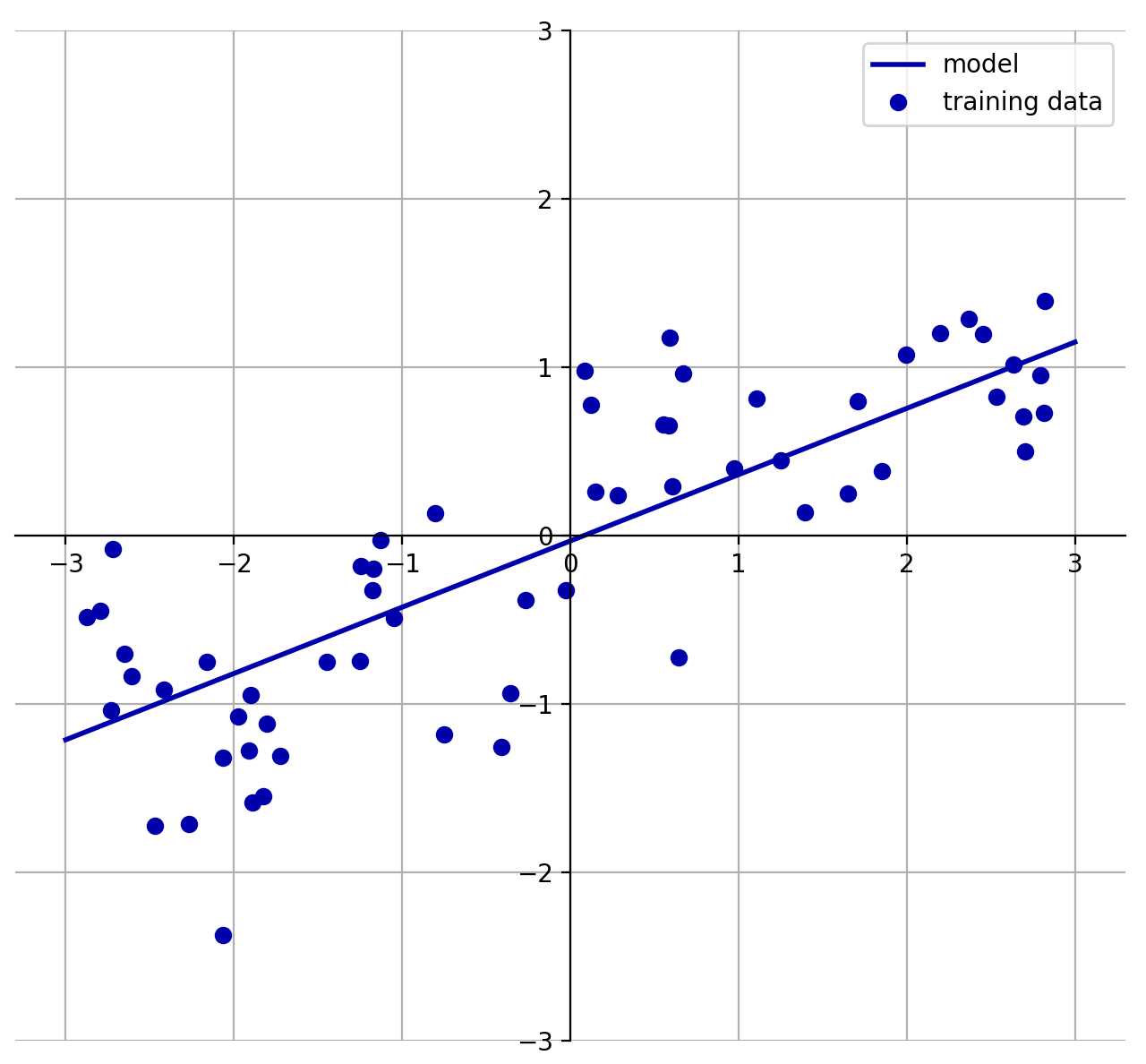
如下图所示，是一个简单的一维数据线性拟合图。

算法

本文的算法均使用python中的scikit-learn实现。scikit-learn是一个非常流行的工具，也是最有名的python机器学习库。它广泛应用于工业界和学术界，网上有大量的教程和代码片段。

针对用于回归的线性模型主要有如下三种求解算法：
1.线性回归(又名普通最小二乘法)
线性回归，或者普通最小二乘法(ordinary least squares，OLS)，是回归问题最简单也最经典的线性方法。线性回归寻找参数w和b，使得对训练集的预测值与真实的回归目标值y之间的均方误差最小。均方误差（mean squared error）是预测值与真实值之差的平方和除以样本数。线性回归没有参数，这是一个优点，但也因此无法控制模型的复杂度。
实现代码如下：

from sklearn.linear_model import LinearRegression 
lr = LinearRegression()  # 构建线性模型
lr.fit(X_train, y_train)  # 拟合数据

“斜率”参数(w，也叫作权重或系数)被保存在coef_属性中，而偏移或截距(b)被保存在 intercept_ 属性中：

print("lr.coef_: {}".format(lr.coef_))
print("lr.intercept_: {}".format(lr.intercept_))

intercept_属性是一个浮点数，而 coef_属性是一个numpy数组，每个元素对应一个输入特征。
score函数可以返回模型的性能：

print("Training set score: {:.2f}".format(lr.score(X_train, y_train)))
print("Test set score: {:.2f}".format(lr.score(X_test, y_test)))

🔔在scikit-learn中基本所有的机器学习算法都用score函数返回模型的性能，返回值是一个0到1之间的浮点数。
对于回归问题，score的返回值是R^2(R方)，其含义是，预测值解释了 y变量的方差的多大比例，衡量的是预测值对于真值的拟合好坏程度。总之就是，值越大，拟合度越高。
对于分类问题，score的返回值是精度，即正确分类的样本在所有样本中所占的比例。

2.岭回归
岭回归也是一种用于回归的线性模型，因此它的预测公式与普通最小二乘法相同。但在岭回归中，对系数(w)的选择不仅要在训练数据上得到好的预测结果，而且还要拟合附加约束。我们还希望系数尽量小。换句话说，w的所有元素都应接近于 0。直观上来看，这意味着每个特征对输出的影响应尽可能小（即斜率很小），同时仍给出很好的预测结果。这种约束是所谓正则化（regularization）的一个例子。正则化是指对模型做显式约束，以避免过拟合。岭回归用到的这种被称为 L2正则化。
L2正则化公式如下：
$$\sum _{i=1}{w}_i^2\le C$$
上式是对 w 的平方和做数值上界限定，即所有w 的平方和不超过参数 C。由L2正则化即可控制所有w接近于0。
岭回归在linear_model.Ridge中实现，代码如下：

from sklearn.linear_model import Ridge
ridge = Ridge().fit(X_train, y_train)
print("Training set score: {:.2f}".format(ridge.score(X_train, y_train)))
print("Test set score: {:.2f}".format(ridge.score(X_test, y_test)))

岭回归算法在模型的简单性(系数都接近于 0)与训练集性能之间做出权衡。简单性和训练集性能二者对于模型的重要程度可以由用户通过设置alpha参数来指定。在前面的例子中,我们用的是默认参数alpha=1.0。但没有理由认为这会给出最佳权衡。alpha 的最佳设定值取决于用到的具体数据集。增大 alpha 会使得系数更加趋向于 0，从而降低训练集性能，但可能会提高泛化性能。
alpha参数的使用方式如下：

ridge10 = Ridge(alpha=10).fit(X_train, y_train)
print("Training set score: {:.2f}".format(ridge10.score(X_train, y_train)))
print("Test set score: {:.2f}".format(ridge10.score(X_test, y_test)))

减小alpha可以让系数受到的限制更小，而对于非常小的 alpha 值，系数几乎没有受到限制，我们会得到一个与线性回归类似的模型。

🔔如果有足够多的训练数据，正则化会变得不那么重要，且模型将更加难以拟合所有的数据。

3.Lasso
除了岭回归，还有一种正则化的线性回归是Lasso。与岭回归相同，使用Lasso也是约束系数使其接近于0，但用到的方法不同，叫作L1 正则化。L1正则化的结果是，使Lasso某些系数刚好为0。这说明某些特征被模型完全忽略。这可以看作是一种自动化的特征选择。某些系数刚好为0，这样模型更容易解释，也可以呈现模型最重要的特征。
L1正则化公式如下：
$$\sum _{i=1}|w_i|\le C$$

from sklearn.linear_model import Lasso
lasso = Lasso().fit(X_train, y_train)
print("Training set score: {:.2f}".format(lasso.score(X_train, y_train)))
print("Test set score: {:.2f}".format(lasso.score(X_test, y_test)))

与岭回归类似，Lasso也有一个正则化参数alpha，可以控制系数趋向于0的强度。此外，Lasso还有一个max_iter参数，即运行迭代的最大次数。
alpha、max_iter参数的使用方式如下：

lasso001 = Lasso(alpha=0.01, max_iter=100000).fit(X_train, y_train)
print("Training set score: {:.2f}".format(lasso001.score(X_train, y_train)))
print("Test set score: {:.2f}".format(lasso001.score(X_test, y_test)))

🔔在实践中，在两个模型中一般首选岭回归。但如果特征很多，你认为只有其中几个是重要的，那么选择Lasso可能更好。同样，如果你想要一个容易解释的模型，Lasso可以给出更容易理解的模型，因为它只选择了一部分输入特征。scikit-learn还提供了 ElasticNet类，结合了Lasso和岭回归的惩罚项。在实践中，这种结合的效果最好，不过代价是要调节两个参数：一个用于L1正则化，一个用于L2正则化。这里不做过多介绍，感兴趣的同学可以自己查阅资料。

用于分类的线性模型

二分类

线性模型也广泛应用于分类问题。我们首先来看二分类。这时可以建立以下模型：
$$y^{\ast }=w_0\ast x_0+w_1\ast x_1+...+w_n\ast x_n+b>0$$
这个模型看起来与线性回归的模型非常相似，但我们没有返回特征的加权求和，而是为预测设置了阈值(0)。如果函数值小于0，我们就预测类别-1；如果函数值大于0，我们就预测类别+1。对于所有用于分类的线性模型，这个预测规则都是通用的。同样，有很多种不同的方法来找出系数(w)和截距(b)。
最常见的两种线性分类算法是Logistic回归(logistic regression)和线性支持向量机(linear support vector machine，线性SVM)，前者在linear_model.LogisticRegression中实现，后者在svm.LinearSVC(SVC代表支持向量分类器)中实现。

🔔虽然Logistic回归的名字中含有回归（regression），但它是一种分类算法，并不是回归算法，不应与线性回归混淆。
由于Logistic回归和线性支持向量机较复杂，本文只介绍其在python中的使用方法。

Logistic回归

from sklearn.linear_model import LogisticRegression
lr_l1 = LogisticRegression(C=C, penalty="l1").fit(X_train, y_train)
print("Training accuracy of l1 logreg with C={:.3f}: {:.2f}".format(C, lr_l1.score(X_train, y_train)))
print("Test accuracy of l1 logreg with C={:.3f}: {:.2f}".format(C, lr_l1.score(X_test, y_test)))

线性支持向量机

from sklearn.svm import LinearSVC
linear_svm = LinearSVC(C=C, penalty="l1").fit(X_train, y_train)
print("Training accuracy of svm logreg with C={:.3f}: {:.2f}".format(C, linear_svm.score(X_train, y_train)))
print("Test accuracy of svm logreg with C={:.3f}: {:.2f}".format(C, linear_svm.score(X_test, y_test)))

🔔参数penalty是正则化方式。
注意，两个模型都默认使用L2正则化，就像岭回归对回归线性模型所做的那样。

对于Logistic回归和线性支持向量机，决定正则化强度的权衡参数叫作C。C值越大，对应的正则化越弱。换句话说，如果参数C值较大，那么Logistic回归和线性支持向量机将尽可能将训练集拟合到最好，而如果C值较小，那么模型更强调使系数向量(w)接近于 0。

如果想要一个可解释性更强的模型，使用L1正则化可能更好，因为它约束模型只使用少数几个特征。

用于二分类的线性模型与用于回归的线性模型有许多相似之处。与用于回归的线性模型一样，模型的主要差别在于penalty参数，这个参数会影响正则化，也会影响模型是使用所有可用特征还是只选择特征的一个子集。

多分类

许多线性分类模型只适用于二分类问题，不能轻易推广到多类别问题（除了Logistic回归）。将二分类算法推广到多分类算法的一种常见方法是“一对其余”(one-vs.-rest)方法。在“一对其余”方法中，对每个类别都学习一个二分类模型，将这个类别与所有其他类别尽量分开，这样就生成了与类别个数一样多的二分类模型。在测试点上运行所有二类分类器来进行预测。在对应类别上分数最高的分类器“胜出”，将这个类别标签返回作为预测结果。
多分类Logistic回归背后的数学与“一对其余”方法稍有不同，但它也是对每个类别都有一个系数向量和一个截距，也使用了相同的预测方法。
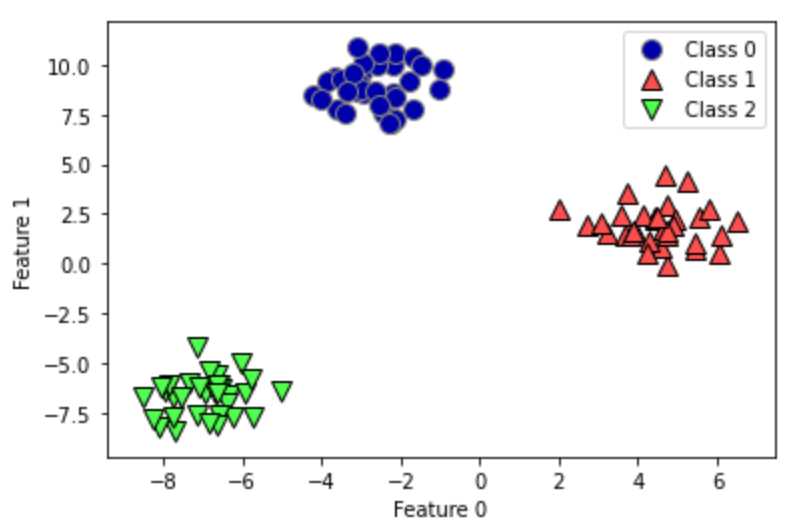
我们将“一对其余”方法应用在一个简单的三分类数据集上。我们用到了一个二维数据集，每个类别的数据都是从一个高斯分布中采样得出的。数据分布如下图所示：

现在，在这个数据集上训练一个SVC分类器：

linear_svm = LinearSVC().fit(X, y)

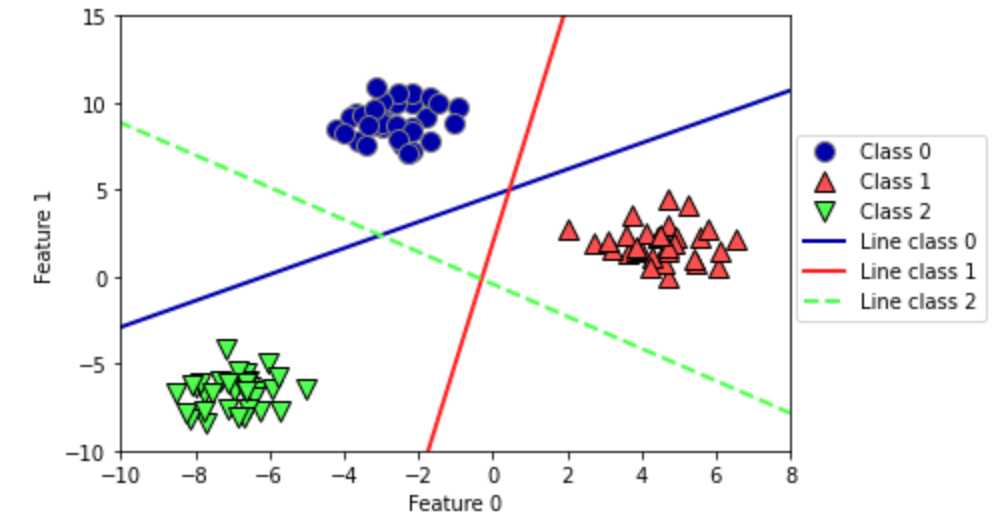
将这 3 个二类分类器给出的直线可视化，如下所示：

import mglearn
import matplotlib.pyplot as plt
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
line = np.linspace(-15, 15)
for coef, intercept, color in zip(linear_svm.coef_, linear_svm.intercept_, ['b', 'r', 'g']):
	plt.plot(line, -(line * coef[0] + intercept) / coef[1], c=color)
plt.ylim(-10, 15)
plt.xlim(-10, 8)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.legend(['Class 0', 'Class 1', 'Class 2', 'Line class 0', 'Line class 1',
		'Line class 2'], loc=(1.01, 0.3))

可以看到，训练集中所有属于类别0的点都在与类别0对应的直线上方，这说明它们位于这个二类分类器属于“类别0”的那一侧。属于类别0的点位于与类别2对应的直线上方，这说明它们被类别2的二类分类器划为“其余”。属于类别0的点位于与类别1对应的直线左侧，这说明类别1的二元分类器将它们划为“其余”。因此，这一区域的所有点都会被最终分类器划为类别0。
但图像中间的三角形区域属于哪一个类别呢，3个二类分类器都将这一区域内的点划为“其余”。这里的点应该划归到哪一个类别呢？答案是分类方程结果最大的那个类别，即最接近的那条线对应的类别。

应用举例（2021国赛B题）

2021年全国大学生数学建模竞赛B题是一道数据分析题，需要分析乙醇耦合制备C4烯烃的实验数据得出结果。其中，第二问要求：分析研究不同温度和催化剂组合对乙醇转化率以及C4烯烃选择性大小的影响。这时，我们就可以构建线性模型对问题进行求解，具体操作如下：

线性回归模型的建立

采用线性模型拟合8个特征与乙醇转化率与C4烯烃的选择性的关系，由此分析对乙醇转化率与C4烯烃的选择性影响最大的特征，令 zi(i =1,2…8) 为第i 个特征，y1为乙醇转化率，y2为C4烯烃选择性，由此我们建立乙醇转化率与C4烯烃选择性的线性模型，模型如下：
$$y_i=k_1\ast z_1+k_2\ast z_2+...+k_8\ast z_8+b,(i=1,2)$$
ki(i=1,2…8)为8个特征的权重，通过权重ki与特征zi来表示乙醇转化率 y1和C4烯烃选择性y2，b表示截距。

线性回归模型的求解

为使得对训练数据集的拟合值yi与乙醇转化率y1和C4烯烃选择性y2真实值方差之间的均方误差最小，采用岭回归算法对上述线性模型进行求解，寻找合适的权重ki和参数b。为同时满足反映结果达到较好且使得权重尽可能小，运用岭回归算法进行求解，利用L2正则化对权重ki进行约束。
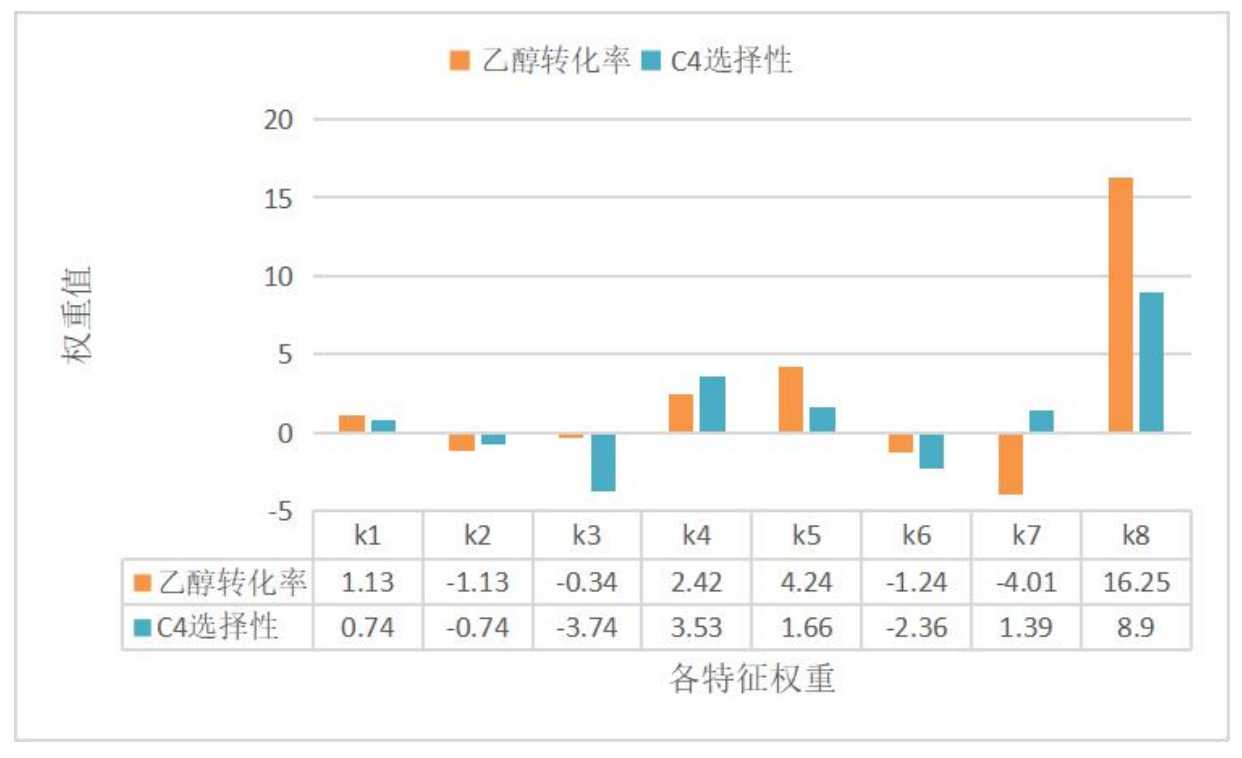
将线性模型代入 python 程序求解，当alpha=8时，乙醇转化率的线性模型拟合度达到最大；当alpha=7时，C4烯烃选择性的线性模型拟合度达到最大。乙醇转化率与C4烯烃选择性的线性模型权重值如下图所示。

由图可得，温度特征的权重值最大，说明温度对乙醇转化率与C4选择性影响最大。装料方式Ⅰ比装料方式Ⅱ更有利于乙醇偶合制备C4烯烃。在催化剂组合中的Co/SiO2质量对C4选择性影响最大，HAP质量对乙醇转化率影响最大。

总结

1. 线性模型的主要参数是正则化参数，在回归模型中叫作alpha，在 Logistic回归和线性支持向量机中叫作C。alpha值较大或C值较小，说明模型比较简单。特别是对于回归模型而言，调节这些参数非常重要。通常在对数尺度上对C和alpha进行搜索。你还需要确定的是用L1正则化还是L2正则化。如果你假定只有几个特征是真正重要的，那么你应该用L1正则化，否则应默认使用L2正则化。如果模型的可解释性很重要的话，使用L1也会有帮助。由于L1只用到几个特征，所以更容易解释哪些特征对模型是重要的，以及这些特征的作用。
2. 线性模型的训练速度非常快，预测速度也很快。这种模型可以推广到非常大的数据集，对稀疏数据也很有效。如果你的数据包含数十万甚至上百万个样本，你可能需要研究如何使用Logistic回归和岭回归模型的solver=’sag’选项，在处理大型数据时，这一选项比默认值要更快。其他选项还有SGDClassifier类和SGDRegressor类，它们对本文介绍的线性模型实现了可扩展性更强的版本。
3. 线性模型的另一个优点在于，利用我们之前见过的用于回归和分类的公式，理解如何进行预测是相对比较容易的。不幸的是，往往并不完全清楚系数为什么是这样的。如果你的数据集中包含高度相关的特征，这一问题尤为突出。在这种情况下，可能很难对系数做出解释。
4. 如果特征数量大于样本数量，线性模型的表现通常都很好。它也常用于非常大的数据集，只是因为训练其他模型并不可行。但在更低维的空间中，其他模型的泛化性能可能更好。

今天的文章数学建模三十六计——线性模型分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。