用时间推进法模拟一维线性对流模型

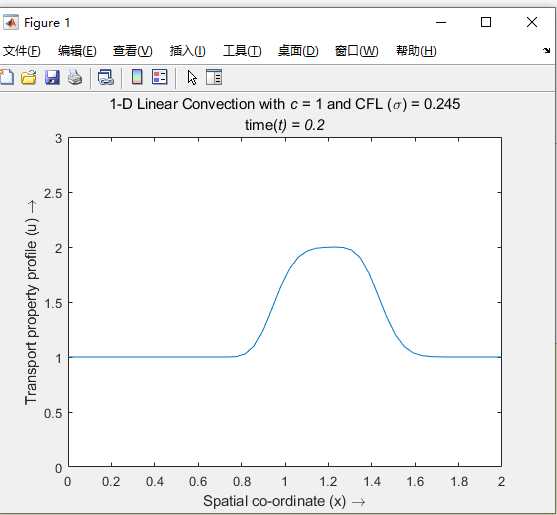
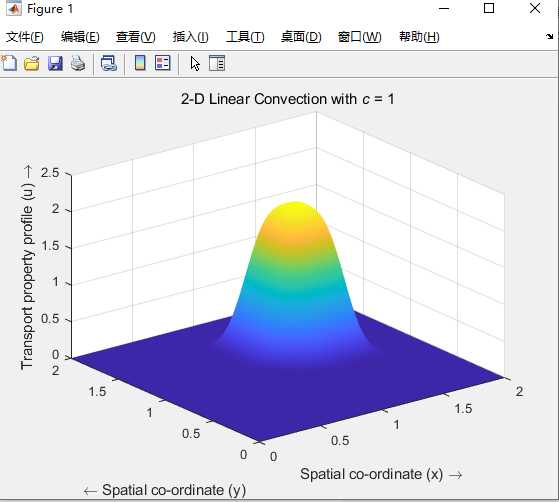
% Simulation of a 1-D Linear Convection model by a time march (Finite
…Difference Method)
% Numerical scheme used is a first order upwind in both space and time

%%
%Specifying Parameters
nx=50;                %Number of steps in space(x)
nt=50;                %Number of time steps 
dt=0.01;              %Width of each time step
c=1.0;                %Velocity of wave propagation
dx=2/(nx-1);          %Width of space step
x=0:dx:2;             %Range of x (0,2) and specifying the grid points
u=zeros(1,nx);        %Preallocating u
un=zeros(1,nx);       %Preallocating un
sigma=abs(c)*dt/dx;   %Courant-Freidrich-Lewy number

%%
%Initial Conditions: A square wave
for i=1:nx
    if ((0.75<=x(i))&&(x(i)<=1.25))
        u(i)=2;
    else
        u(i)=1;
    end
end

%%
%Evaluating velocity profile for each time step
i=2:nx-1;
for it=0:nt
    un=u;
    h=plot(x,u);       %plotting the velocity profile
    axis([0 2 0 3])
    title({[‘1-D Linear Convection with {\itc} = ‘,num2str(c),’ and CFL (\sigma) = ‘,num2str(sigma)];[‘time(\itt) = ‘,num2str(dt*it)]})
    xlabel(‘Spatial co-ordinate (x) \rightarrow’)
    ylabel(‘Transport property profile (u) \rightarrow’)
    drawnow;
    refreshdata(h)
    pause(0.1)
    %Explicit method with F.D in time and B.D in space
    u(i)=un(i)-0.5*(sign(c)+1)*((c*dt*(un(i)-un(i-1)))/dx)…
        +0.5*(sign(c)-1)*((c*dt*(un(i+1)-un(i)))/dx);
end

 D143

今天的文章用时间推进法模拟一维线性对流模型分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。