1 Polar 码编码
1.1 信道极化
1.2 编码
1.3 相关例子
1.3.1BEC信道
1.3.2信道联合极化编码思想
2 SC译码算法
2.1 SC译码算法
2.2 LLR,f函数和g函数
3 言外之笔
1 Polar 码编码
1.1信道极化
2009年在“IEEETransaction on Information Theory”期刊上发表论文详细地阐述了信道极化,并基于信道极化给出了一种新的编码方式,名称为极化码。从代数编码的角度来说,只要给定编码长度,极化码的编译码结构就唯一确定了;从概率编码的角度来说,极化码在设计时,利用了信道联合与信道分裂的过程来选择具体的编码方案,而且在译码时也是采用概率算法。
信道极化是一种现象,把它看作一种原理,而极化码编码则是对这一原理的应用。从宏观的角度观察,信道联合是把信道极化过程看作一个整体,输入是比特,输出也是比特。但只有信道联合是不够的,无法确知各个子信道的输入和输出是什么关系。于是就需要对信道极化过程有一个微观的表达,这个微观表达是通过信道分裂过程来实现的。宏观和微观合在一起就构成了对信道极化过程的完整表达。在实际中,可以采用递归式来计算各个分裂子信道的转移概率。
通过信道的联合与分裂,各个子信道的对称容量将呈现两级分化的趋势,随着码长的增加,一部分子信道的容量趋于1,而其余子信道的容量趋于0。极化码正是利用这一信道极化的现象,在容量趋于1的个子信道上传输消息比特,在其余子信道上传输冻结比特。
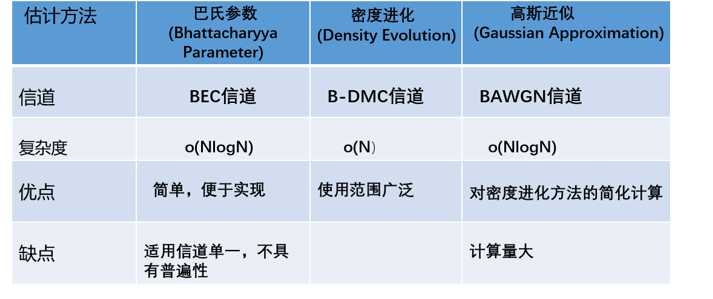
在极化码编码时,首先要区分出分裂信道的可靠程度,可靠度高的信道传输信息比特,可靠度低的传输“冻结比特”,而对各个极化信道的可靠性进行度量常用的有三种方法:巴氏参数法、密度进化法和高斯近似法。
具体表格如下:
2016年,华为提出了一种β-expansion算法,并且证实β-expansion方法以低复杂度获得了与GA相同的性能,提供了一种整洁、复杂度低的方法来排序信道的可靠度。
1.2 编码
总体而言,极化编码的步骤主要由以下三部分构成:极化信道可靠性估计、比特混合以及构造生成矩阵。
不同的信道,信道估计的方法也不太相同,如图1所示;比特混合,简而言之,对于码率为K/N的极化码,选择可靠性最大的K个分裂子信道传输消息比特,其他分裂子信道传输冻结比特,冻结比特一般为“0”。
生成矩阵可表示为:





1.3 相关例子
1.3.1 BEC 信道
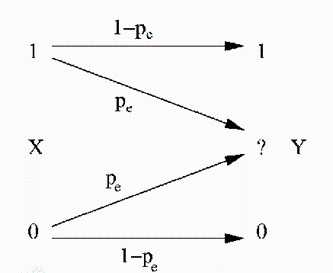
发送方仅仅发送0或者1,信道的擦除概率为Pe,接收端只有两种情况:得到其本身或是丢失,不会出现误码的情况,容易得到信道容量C= 1−Pe。
简化为:
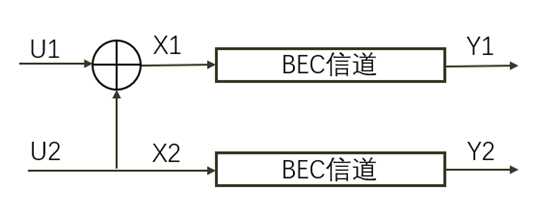
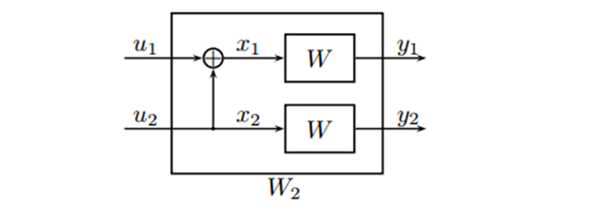
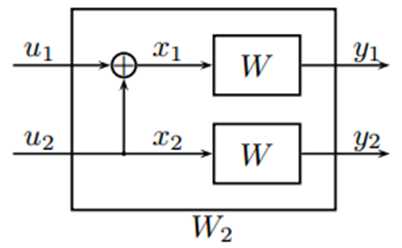
1.3.2 信道联合极化编码思想
由上图,可以得知:
在解码一端,如果能够正确接收,则有:
根据异或的性质,反解出U1,U2:
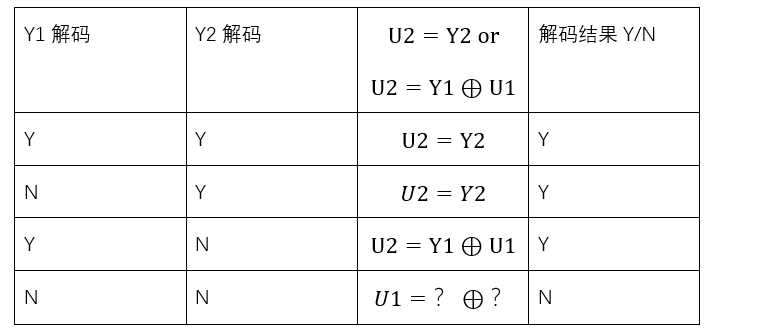
以下分析两条信道的具体情况:
对于第一条信道U1:
Y代表成功,N代表失败。
取Pe=0.5,则传输成功的概率 P = (1−Pe)×(1−Pe)=(1−Pe)^2= 0.25,被擦除的概率P = 1−(1−Pe)^2 = 0.75;
对于第一条信道U2:
Y代表成功,N代表失败。
取Pe=0.5,则传输成功的概率 P = 1−Pe^2= 0.75;被擦除的概率P =1-( 1−Pe^2) = Pe^2=0.25;
结论:对于U1来说,创造了一个较差的信道,但是,对于U2来说,创造了一个较好的信道。
其中,U1被擦除的概率为2*Pe-Pe^2,U2被擦除的概率为Pe^2.对于U1而言,当通道1或通道二不能正确传输,无法解码U1;对于U2而言,当通道1和通道二都未能正确传输,无法解码U2;
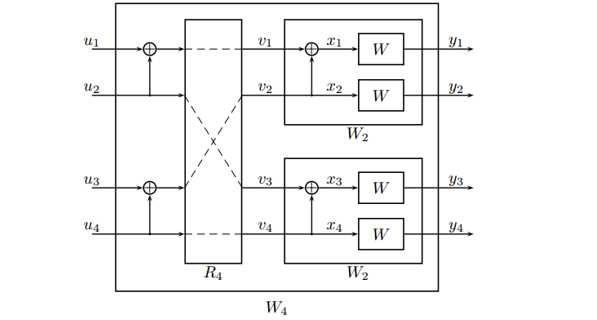
当我们增加更多的通道,可以得到更加理想的通道以及更差的通道。如下图所示:
其中,若Pe=0.5,
U1被擦除的概率为:2*(2*Pe-Pe^2) – (2*Pe-Pe^2) ^2=0.9375
U2被擦除的概率为:(2*Pe-Pe^2) ^2=0.5625
U3被擦除的概率为:2*Pe^2- Pe^4=0.4375
U4被擦除的概率为:(Pe^2) ^2=0.0625
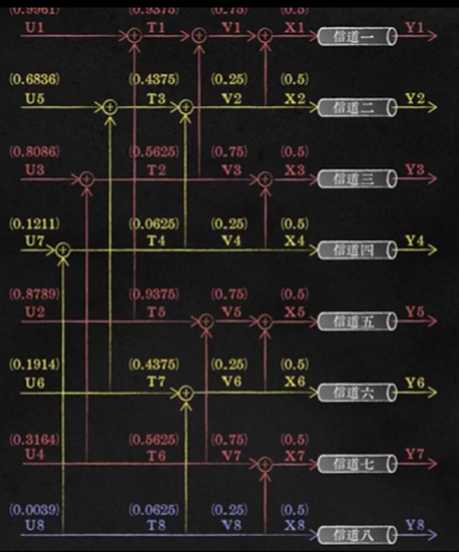
如果是8个通道,查找相关数据,得到如下的结果:
级联八个信道,就会有擦除率为0.0039的信道出现。于是,但信道数N很大的时候,可以得到擦除率极低的可靠信道。
于是,通过信道的联合与分裂,各个子信道的对称容量将呈现两级分化的趋势,随着码长的增加,一部分子信道的容量趋于1,而其余子信道的容量趋于0。极化码正是利用这一信道极化的现象,在容量趋于1的个子信道上传输消息比特,在其余子信道上传输冻结比特,冻结比特都是通信双方事先约定好的比特,一般是“0”。
2 SC译码算法
2.1 SC译码算法
串行抵消译码算法,是Arikan给出的Polar Code译码算法,由于各个极化信道并不是相互独立的,而是具有确定的依赖关系的:信道序号大的极化信道依赖于所有比其序号小的极化信道。基于极化信道之间的这一依赖关系,SC译码算法对各个比特进行译码判决时,需要假设之前步骤的译码得到的结果都是正确的。当前面消息比特的译码中发生错误之后,由于SC译码器在对后面的消息比特译码时需要用到之前的消息比特的估计值,这就会导致较为严重的错误传递。因此,对于有限码长的极化码,采用SC译码器往往不能达到理想的性能。
大概的算法思路流程如下:
(1)在接收到传输的序列之后,先将其初始化,得到单个信道的似然比;
(2)计算估计码字的似然值,判决码字
(3)终止判断,输出码字。
在SC译码算法中,LLR的递归运算需要借助f函数和g函数。以下会详细给出。
当引入高斯近似法,接收符号y的对数似然比(LLR)定义为:
因此译码端对数似然比的初始值可以轻松得到。相比于SC译码算法,极化码的译码算法还有SCL译码,CRC辅助译码,还有BP译码算法等算法。
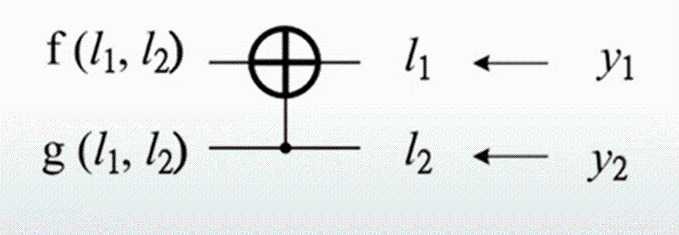
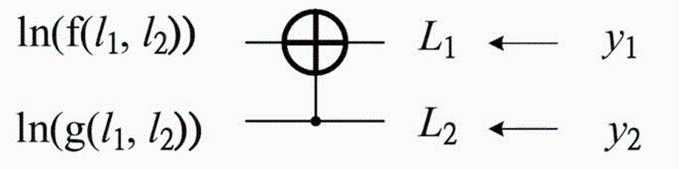
2.2 LLR,f函数和g函数
采取硬判决:
其中:
2,
于是有:
此时,译码判决如下:
在上述的计算辅助下,即可完成SC译码,把发送的码字一一译码出来,当然,如果实现约定好冻结比特,可以更快提高译码速度,降低译码时延。
3 言外之笔
1,相关论文若干,在此不一一列举。
2,文中所展示的图片有个人原创,也有网络搜索、非本人原创,若有侵权,请联系删除。
3,在写作过程之中,参考许多前辈的心得,本文仅仅是本人一些拙见愚意,仅供参考,许多错误之处请多多包涵。
今天的文章Polar码的编码思想以及SC译码算法分享到此就结束了,感谢您的阅读,如果确实帮到您,您可以动动手指转发给其他人。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/33549.html