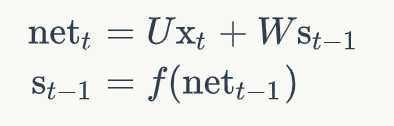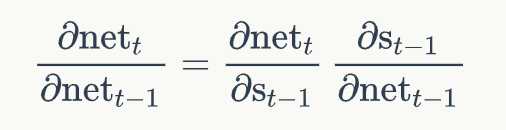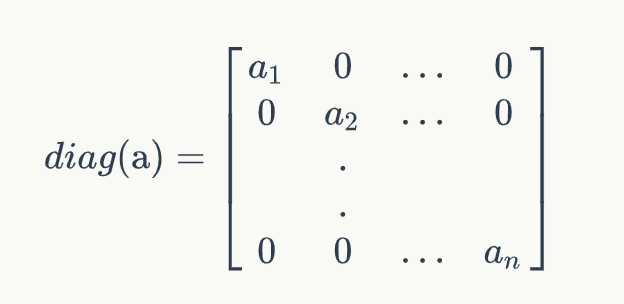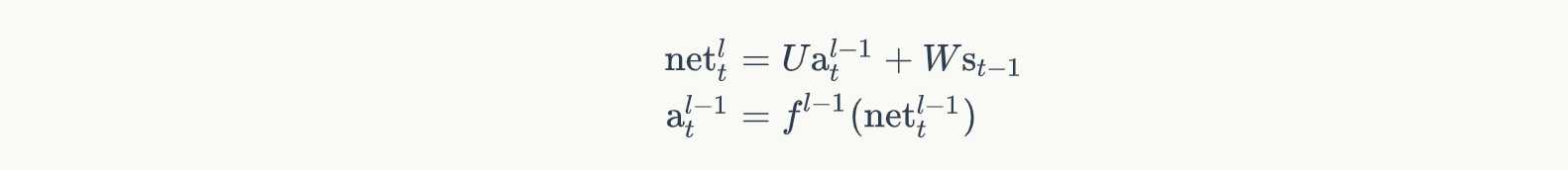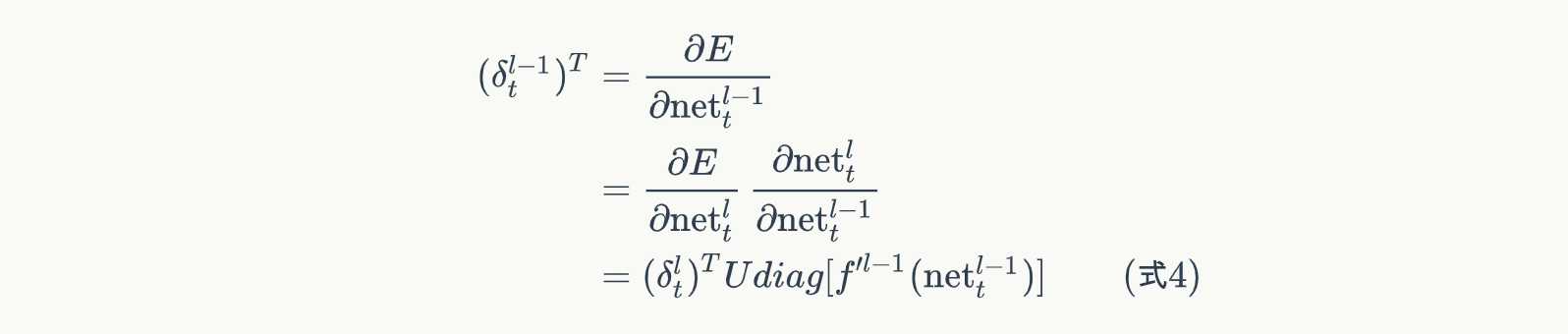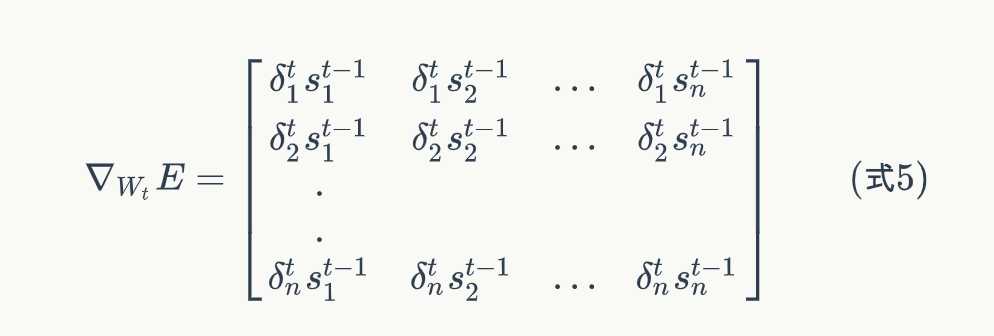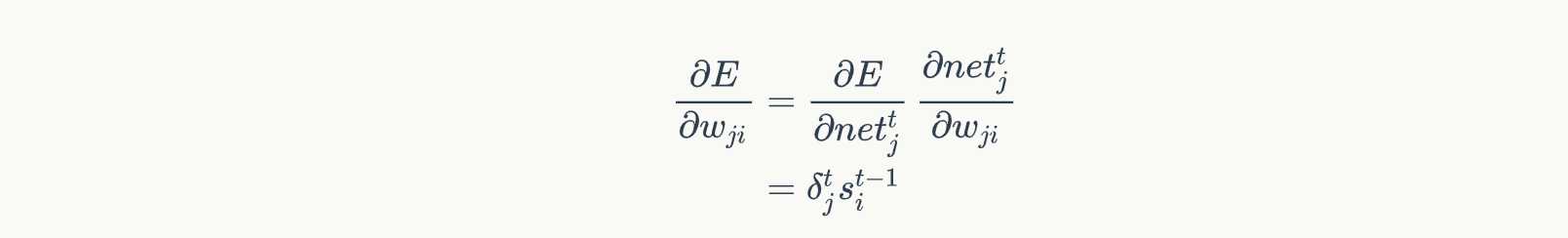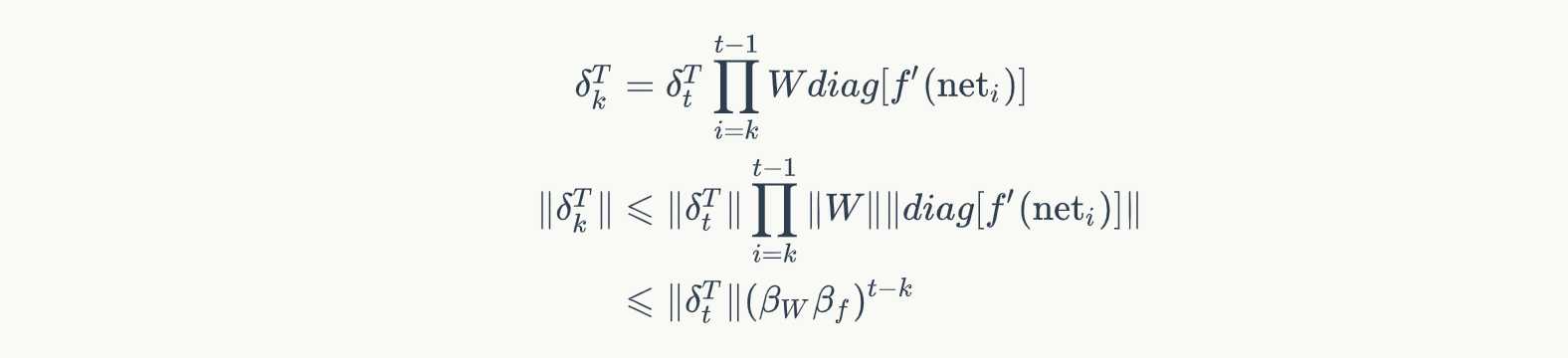前文：循环神经网络——初学RNN https://blog.csdn.net/weixin_38522681/article/details/109129490

基本步骤

BPTT算法是针对循环层的训练算法，它的基本原理和BP算法是一样的，也包含同样的三个步骤：

1.前向计算每个神经元的输出值；
2.反向计算每个神经元的误差项${\delta }_j$值，它是误差函数E对神经元j的加权输入$ne{t}_j$的偏导数；
3.计算每个权重的梯度。
最后再用随机梯度下降算法更新权重。
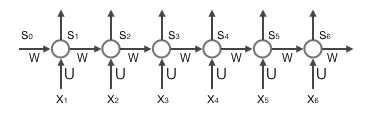
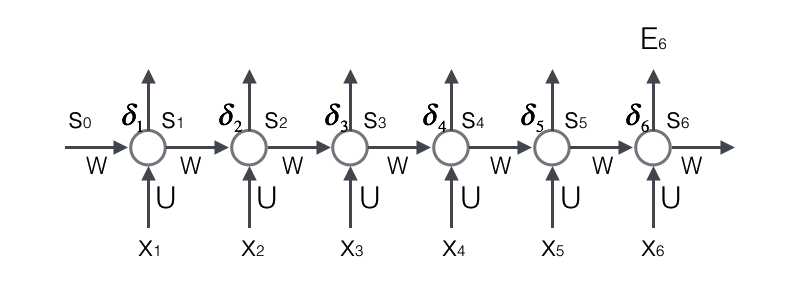
循环层如下图所示：

前向计算

$$s_t=f(U{x}_t+W{s}_{t-1})$$
上面的$s_t$、$x_t$、$s_{t-1}$都是向量，用黑体字母表示；而U、V是矩阵，用大写字母表示。向量的下标表示时刻，例如,$s_t$表示在t时刻向量s的值。
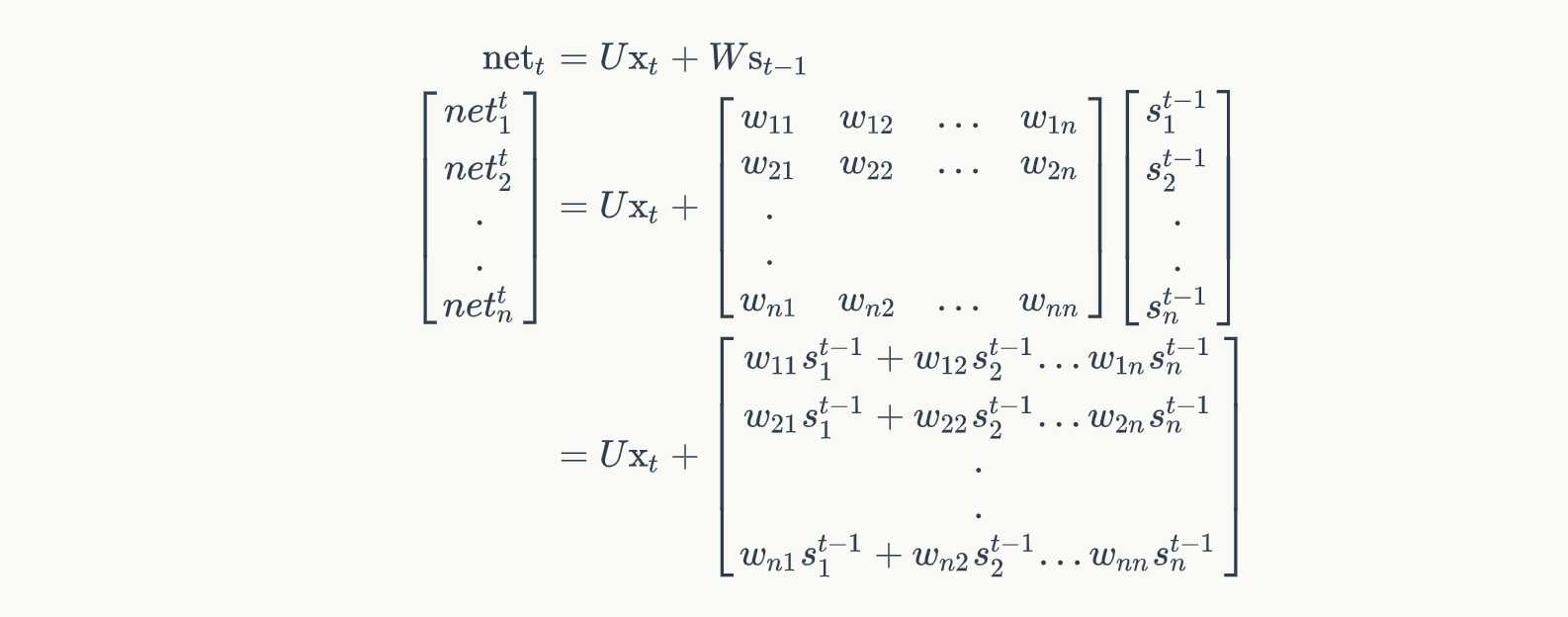
我们假设输入向量x的维度是m，输出向量s的维度是n，则矩阵U的维度是$n\times m$，矩阵W的维度是$n\times n$。下面是上式展开成矩阵的样子，看起来更直观一些：

在这里我们用手写体字母表示向量的一个元素，它的下标表示它是这个向量的第几个元素，它的上标表示第几个时刻。例如，$s_j^t$表示向量s的第j个元素在t时刻的值。$u_{ji}$表示输入层第i个神经元到循环层第j个神经元的权重。$w_{ji}$表示循环层第t-1时刻的第i个神经元到循环层第t个时刻的第j个神经元的权重。

误差项的计算

BTPP算法将第l层t时刻的误差项值${\delta }_j^l$沿两个方向传播，一个方向是其传递到上一层网络，得到${\delta }_j^{l-1}$，这部分只和权重矩阵U有关；另一个是方向是将其沿时间线传递到初始时刻$t_1$，得到${\delta }_j^1$，这部分只和权重矩阵W有关。
我们用向量$ne{t}_t$表示神经元在t时刻的加权输入，因为：


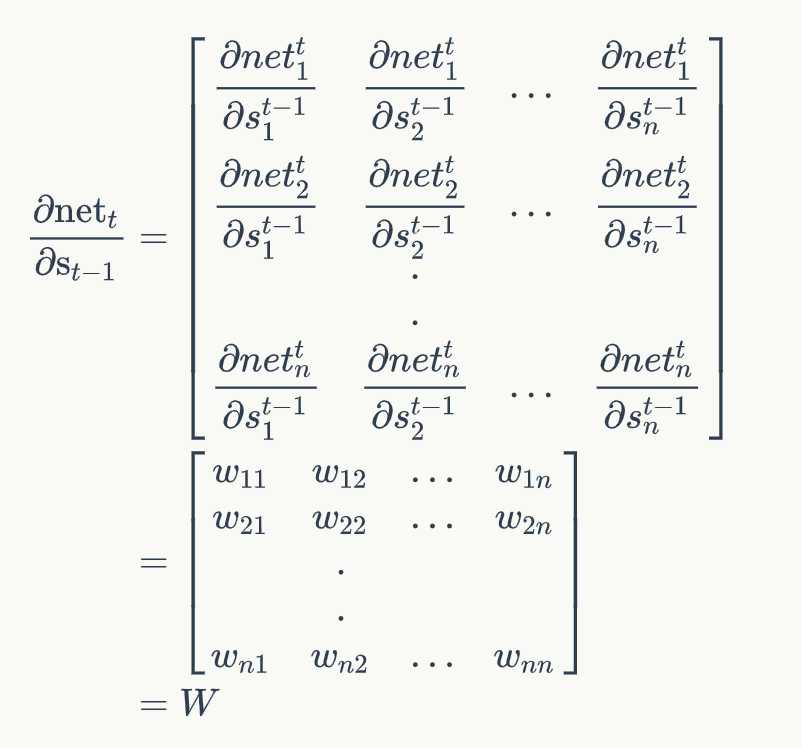
我们用a表示列向量，用$a^T$表示行向量。两项结果为Jacobian矩阵：


其中，diag[a]表示根据向量a创建一个对角矩阵，即

两项结合，得

上式描述了将$\delta$沿时间往前传递一个时刻的规律，有了这个规律，我们就可以求得任意时刻k的误差项${\delta }_k$

式3就是将误差项沿时间反向传播的算法。
循环层将误差项反向传递到上一层网络，与普通的全连接层是完全一样的
循环层的加权输入$ne{t}^l$与上一层$ne{t}^{l-1}$的加权输入关系如下：

所以，

式4就是将误差项传递到上一层算法。

权重梯度的计算

现在，我们终于来到了BPTT算法的最后一步：计算每个权重的梯度。

首先，我们计算误差函数E对权重矩阵W的梯度$\frac{\partial E}{\partial W}$。

只要知道了任意一个时刻的误差项${\delta }_t$，以及上一个时刻循环层的输出值$s_{t-1}$，就可以按照下面的公式求出权重矩阵在t时刻的梯度${\nabla }_{W_t}E$：

式5推导如下

因为对W求导与$U{x}_t$无关，我们不再考虑。现在，我们考虑对权重项$w_{ji}$求导。通过观察上式我们可以看到$w_{ji}$只与$ne{t}_j^t$有关，所以：

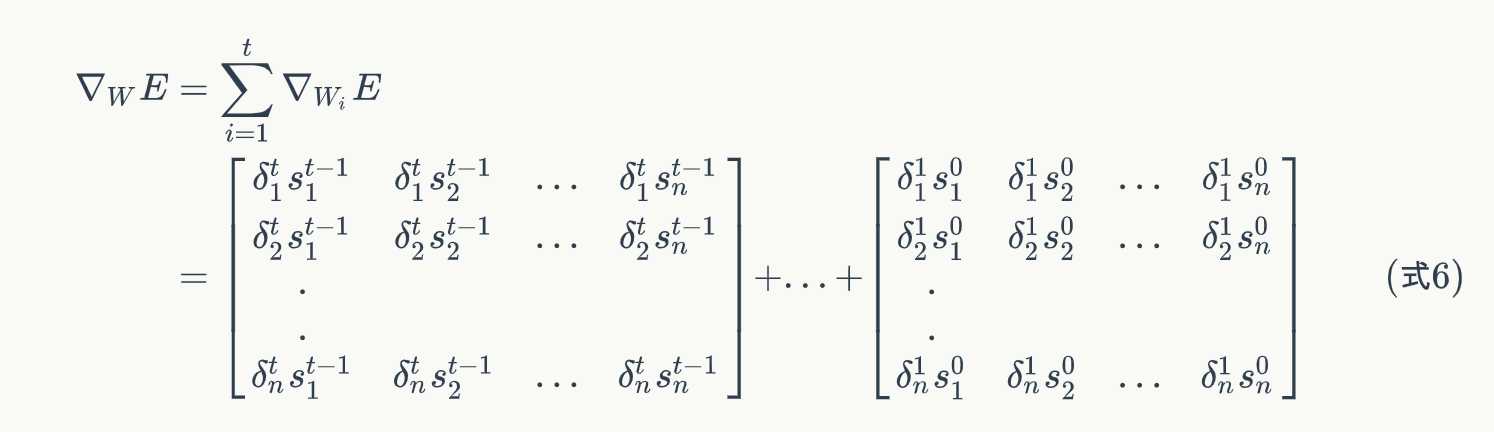
我们已经求得了权重矩阵W在t时刻的梯度${\nabla }_{W_t}E$，最终的梯度${\nabla }_{W}E$是各个时刻的梯度之和，详解见参考

式6就是计算循环层权重矩阵W的梯度的公式。

RNN的梯度爆炸和消失问题

实践中前面介绍的几种RNNs并不能很好的处理较长的序列。一个主要的原因是，RNN在训练中很容易发生梯度爆炸和梯度消失，这导致训练时梯度不能在较长序列中一直传递下去，从而使RNN无法捕捉到长距离的影响。

根据式3可得

上式的$\beta$定义为矩阵的模的上界。因为上式是一个指数函数，如果t-k很大的话（也就是向前看很远的时候），会导致对应的误差项的值增长或缩小的非常快，这样就会导致相应的梯度爆炸和梯度消失问题（取决于$\beta$大于1还是小于1）。

通常来说，梯度爆炸更容易处理一些。因为梯度爆炸的时候，我们的程序会收到NaN错误。我们也可以设置一个梯度阈值，当梯度超过这个阈值的时候可以直接截取。

梯度消失更难检测，而且也更难处理一些。总的来说，我们有三种方法应对梯度消失问题：

1. 合理的初始化权重值。初始化权重，使每个神经元尽可能不要取极大或极小值，以躲开梯度消失的区域。
2. 使用relu代替sigmoid和tanh作为激活函数。
3. 使用其他结构的RNNs，比如长短时记忆网络（LTSM）和Gated Recurrent Unit（GRU），这是最流行的做法。

参考: https://zybuluo.com/hanbingtao/note/541458

今天的文章循环神经网络——RNN的训练算法：BPTT分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。