MATLAB曲线拟合工具箱（cftool）介绍（完结）

本文通过实例对MATLAB曲线拟合工具箱进行详细讲解，帮助大家更容易理解曲线拟合工具箱（cftool）。

1.实例介绍

已知
x = [0 0.2 0.50.8 0.9 1.3 1.4 1.9 2.1 2.2 2.5 2.6 2.9 3.0];
y = [1.27792.1596 2.7311 2.5974 2.4068 1.6215 1.4178 0.9955 0.9666 0.8837 0.9639 1.00311.1233 1.1583];

并且根据某种物理或数学关系确定y=f(x)的表达形式，并求出拟合结果对应的系数。

2. 进入曲线拟合工具箱界面

两种方法，第一种：
打开app栏的曲线拟合工具箱（Curve Fitting），

第二种，直接在命令行窗口输入“cftool”：

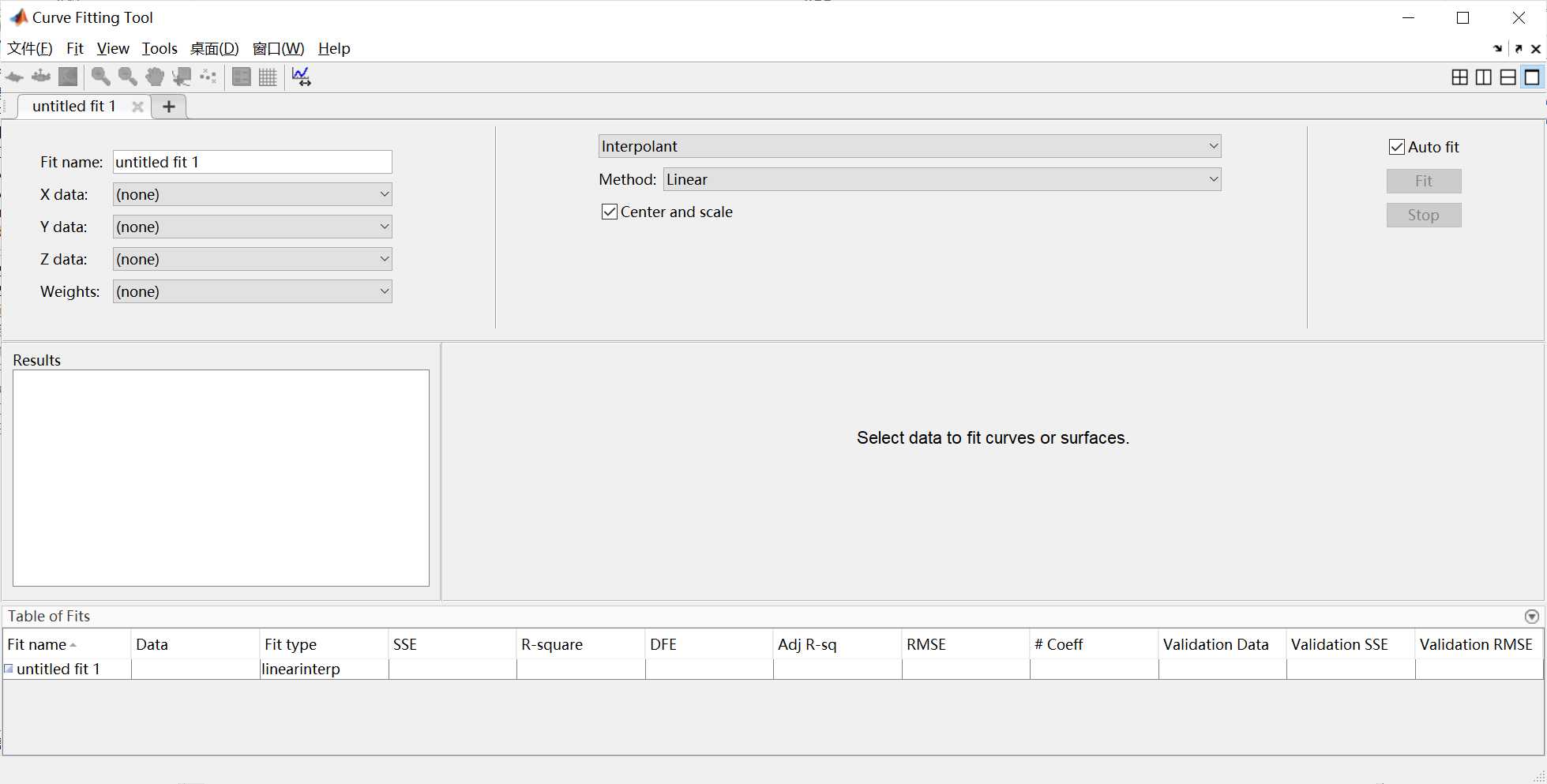
进入界面后，弹出如下窗口：

3. 加载数据

新建一个.m文件，并写入如下代码：

clc;clear;
x = [0 0.2 0.5 0.8 0.9 1.3 1.4 1.9 2.1 2.2 2.5 2.6 2.9 3.0];
y = [1.2779 2.1596 2.7311 2.5974 2.4068 1.6215 1.4178 0.9955 0.9666 0.8837 0.9639 1.0031 1.1233 1.1583];

作为要拟合曲线所需要的数据。

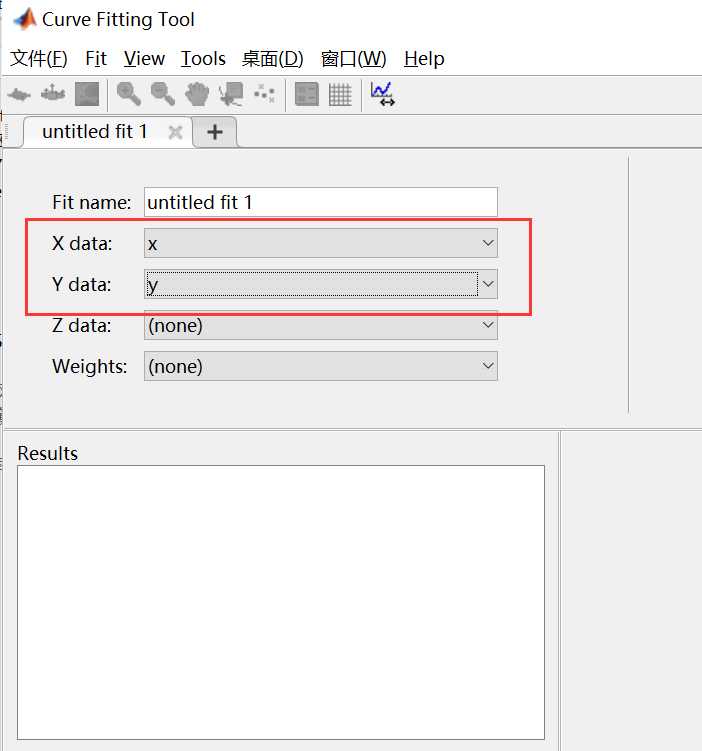
4. 加载数据

在上述窗口中选中相应数据和拟合选项：

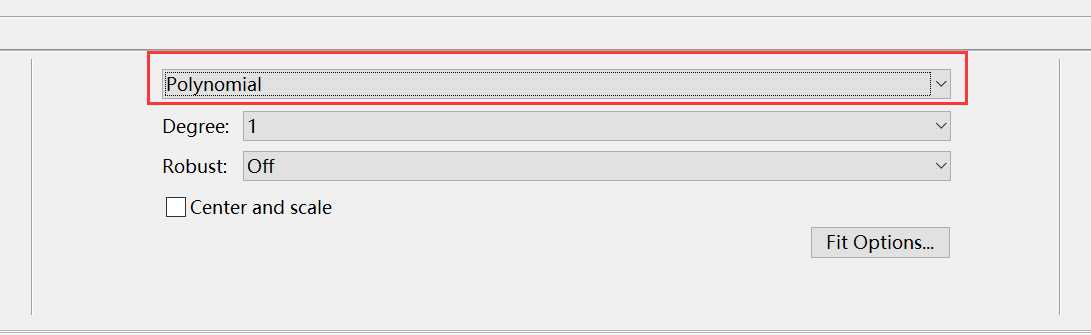
5. 选择拟合曲线的类型

通过下拉菜单选择拟合曲线的类型，

工具箱提供的拟合类型有：

• Custom Equations：用户自定义的函数类型；
• Exponential：指数逼近，有2种类型， $a\ast exp(b\ast x)$ 、 $a\ast exp(b\ast x)+c\ast exp(d\ast x)$；
• Fourier：傅立叶逼近，有7种类型，基础型是 $a0+a1\ast cos(x\ast w)+b1\ast sin(x\ast w)$；
• Gaussian：高斯逼近，有8种类型，基础型是 $a1\ast exp(-((x-b1)/c1{)}^2)$；
• Interpolant：插值逼近，有4种类型，Nearest neighbor、Linear、Cubic、Shape-preserving（PCHIP）；
• Linear Fitting：线性拟合；
• Polynomial：多形式逼近；
• Power：幂逼近，有2种类型，$a\ast x^b$ 、$a\ast x^b+c$；
• Rational：有理数逼近；
• Smoothing Spline：平滑逼近；
• Sum of Sin Functions：正弦曲线逼近，有8种类型，基础型是 $a1\ast sin(b1\ast x+c1)$；
• Weibull：只有一种，$a\ast b\ast x^{(}b-1)\ast exp(-a\ast x^b)$；

6. 进行曲线拟合

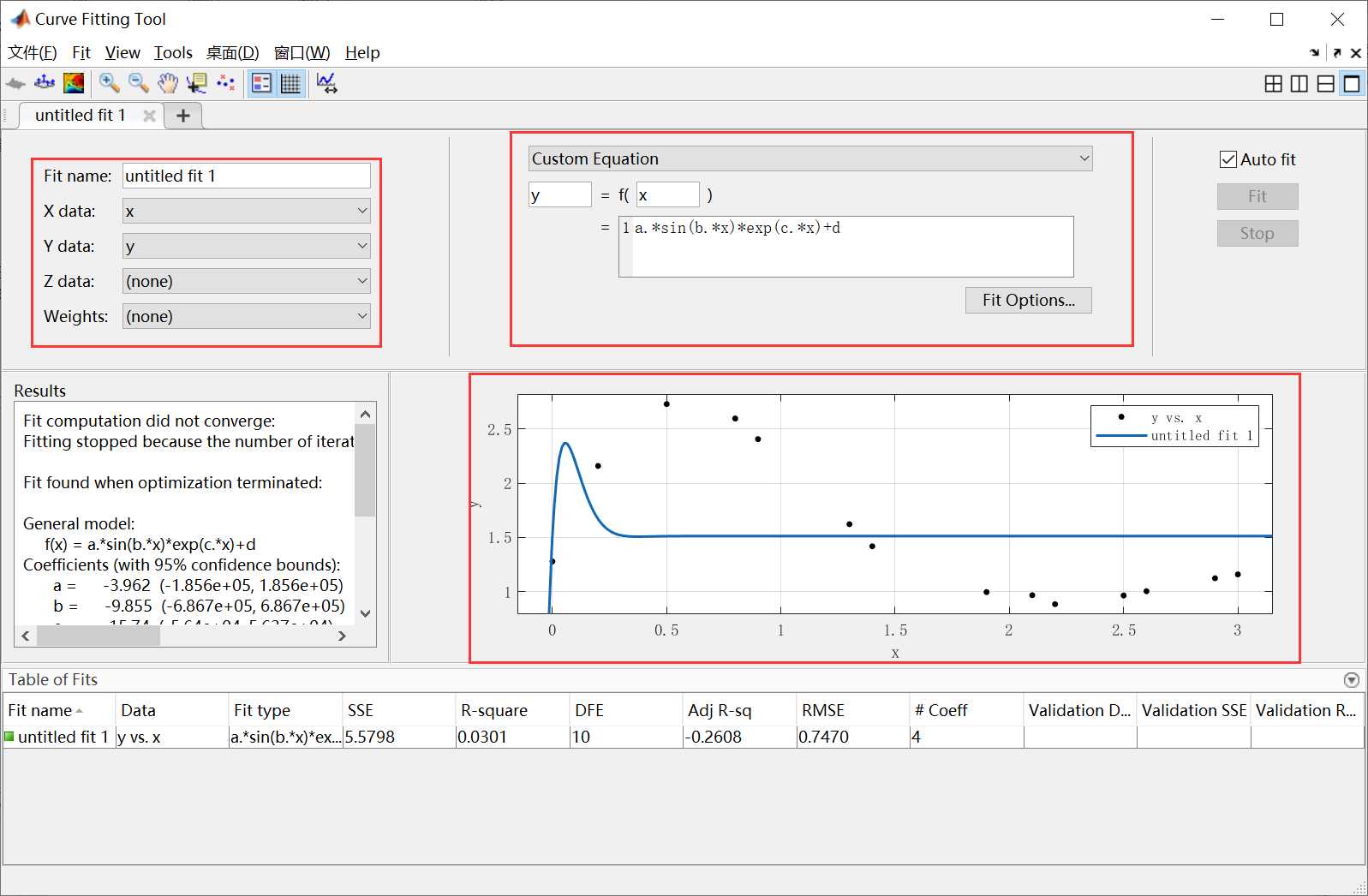
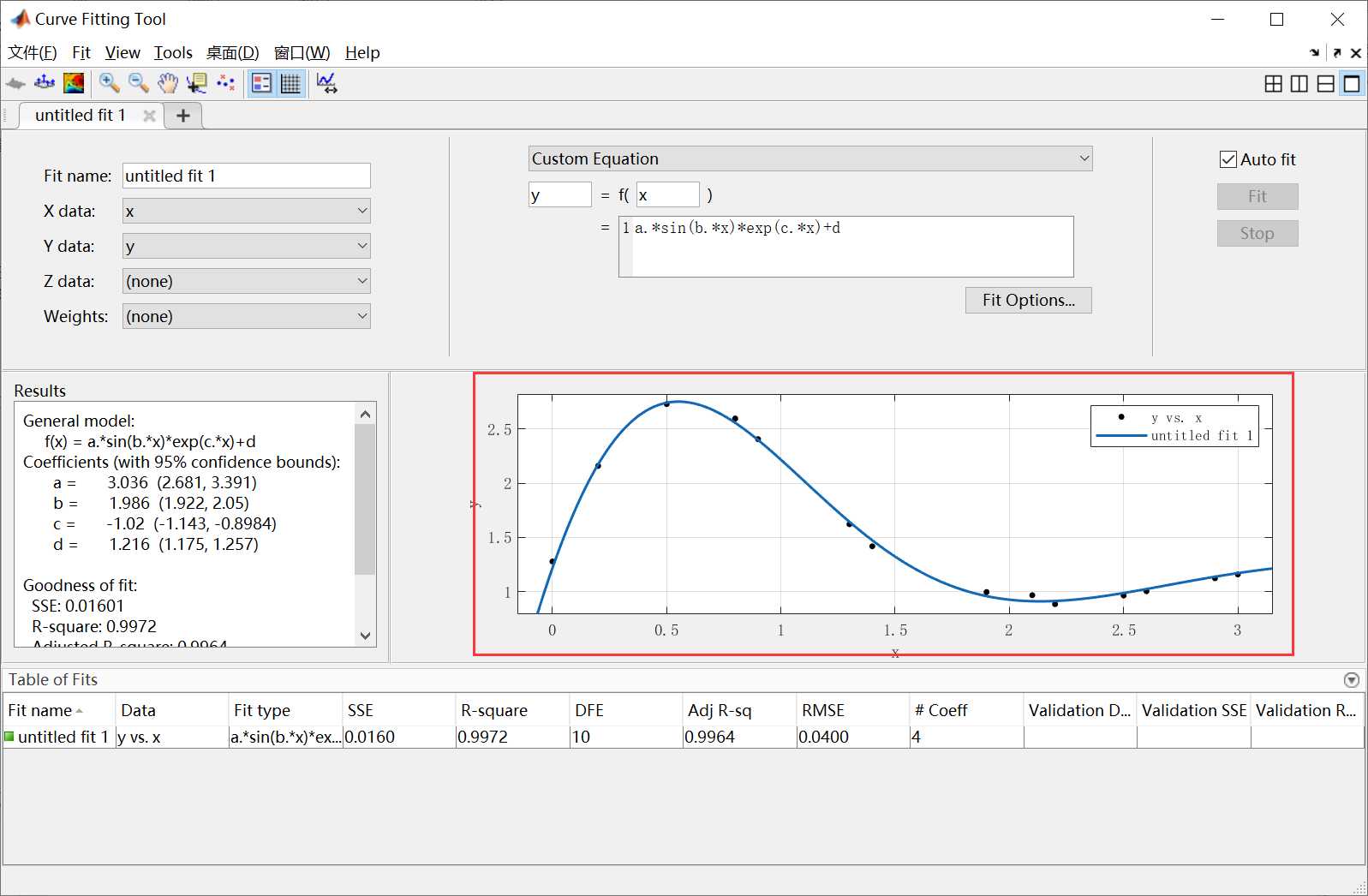
假设我们以$y=a\ast sin(b\ast x)\ast exp(c\ast x)+d$的表达形式进行拟合，则选择”Custom Equation”，在方框中输入相应的函数表达式，拟合过程及结果图像如下图所示：

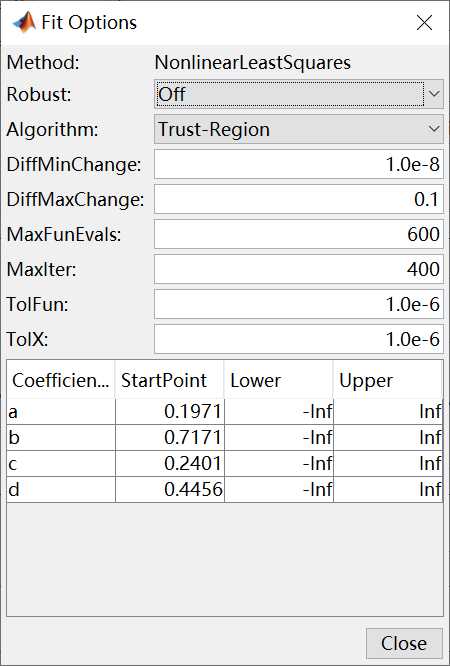
可以发现，曲线和拟合程度较差。这是因为，对同一问题的拟合情况，每次可能都不一样，这取决对于参数a,b,c,d的StartPoint的选取。解决方法是在拟合过程中，将a，b，c和d也作为约束拟合的条件，例子中已知a,b,c,d的的取值范围(正负范围)，可以进行如下操作，点击[Fit Options]按钮，弹出的窗口如下：

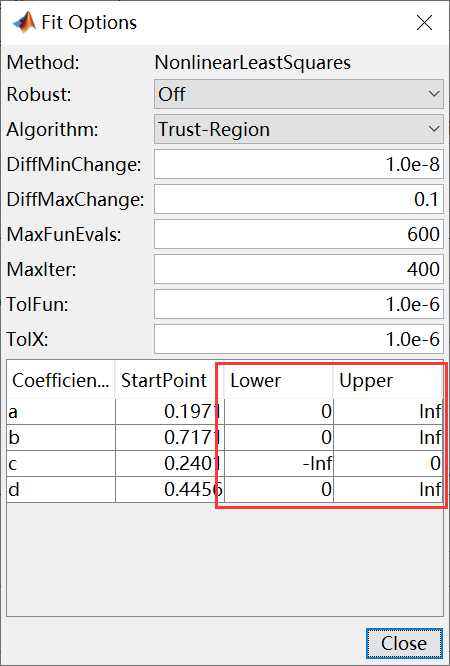
可以调整a,b,c,d参数的StartPoint,Lower,Upper三个选项来是拟合更加准确，比如说，将a,b,d的Lower选项设为0（a,b,d>0），将c的Upper选项设为0（c<0），设置如下图所示：

设置完毕之后，就会自动出现重新拟合之后的图像，如下图所示。

可以看到，拟合程度较之前有了很大的提高.因此，可以预见的是，在拟合过程中，设置好待拟合函数的参数的StartPoint，Lower和Upper三者的值可以使拟合更加准确。

7. 拟合结果分析

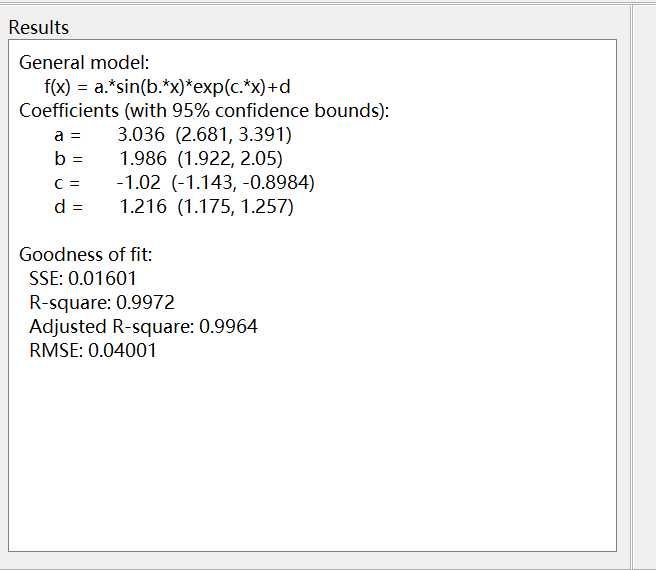
在左侧的Result中显示拟合模型、参数以及拟合效果：

拟合效果评测：

• SSE：拟合误差平方和，接近0，表示与数据拟合的好，但是要小心过拟合；
• R-Square：实测数据与推理数据之间的相关系数平方值，趋近于1较好；
• RMSE：均方差；

8.其他常用拟合方法

当然，除了上面提到的拟合方法之外，还有两种常用的拟合方法：

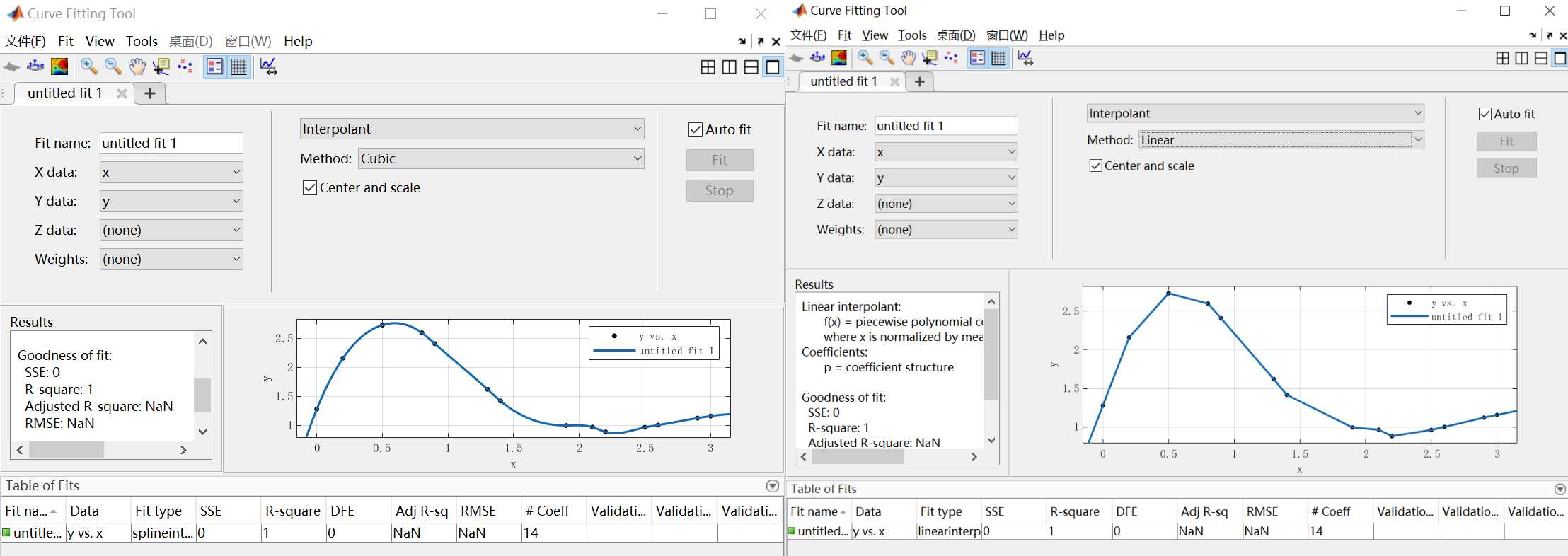
• Interpolant
  插值逼近，该方法的优势在于会连接所有点，而使其SSE为0，R-square为1，如下图所示：
  
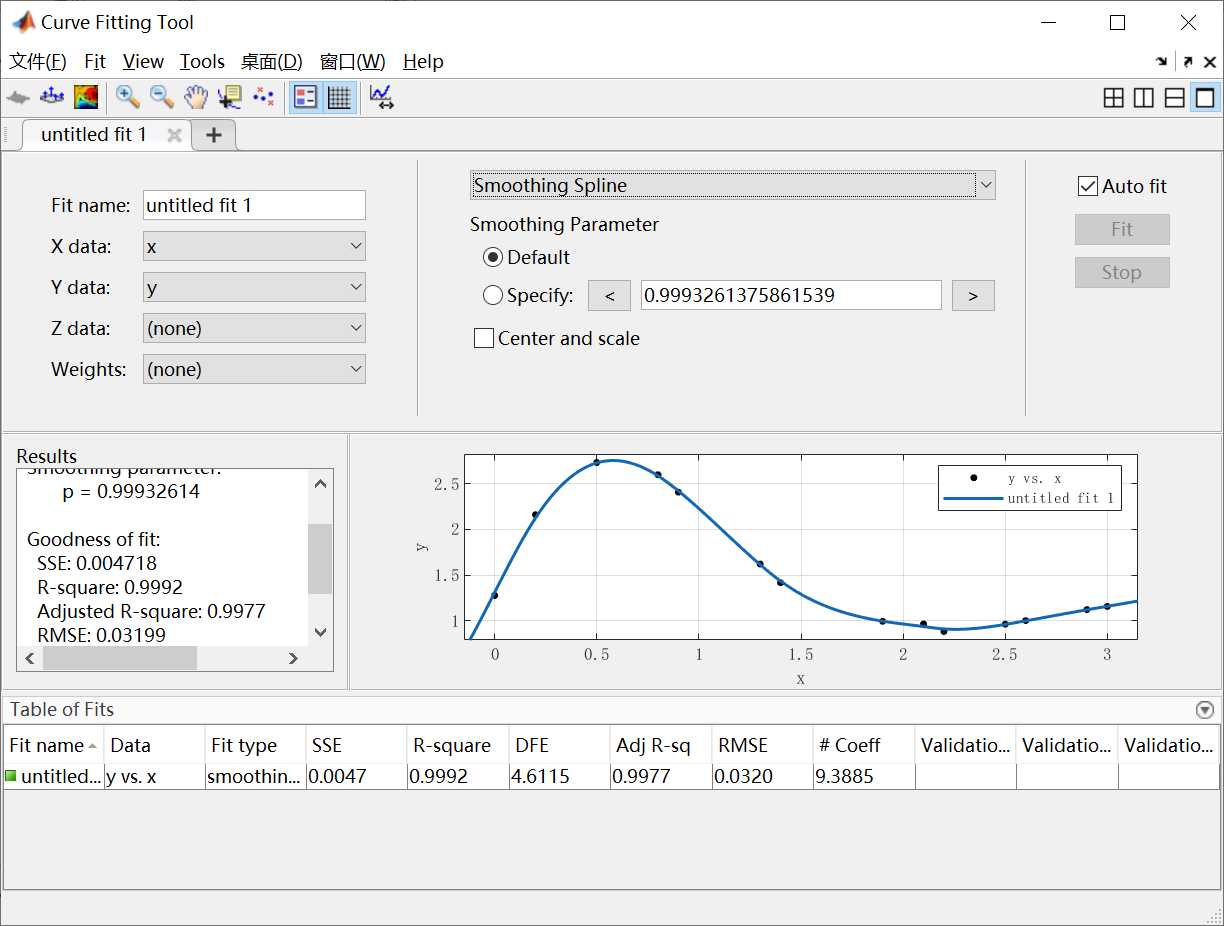
• Smoothing Spline
  平滑逼近，该方法的会尽可能逼近所有点，使其SSE尽可能逼近0，R-square尽可能逼近1，如下图所示：
  

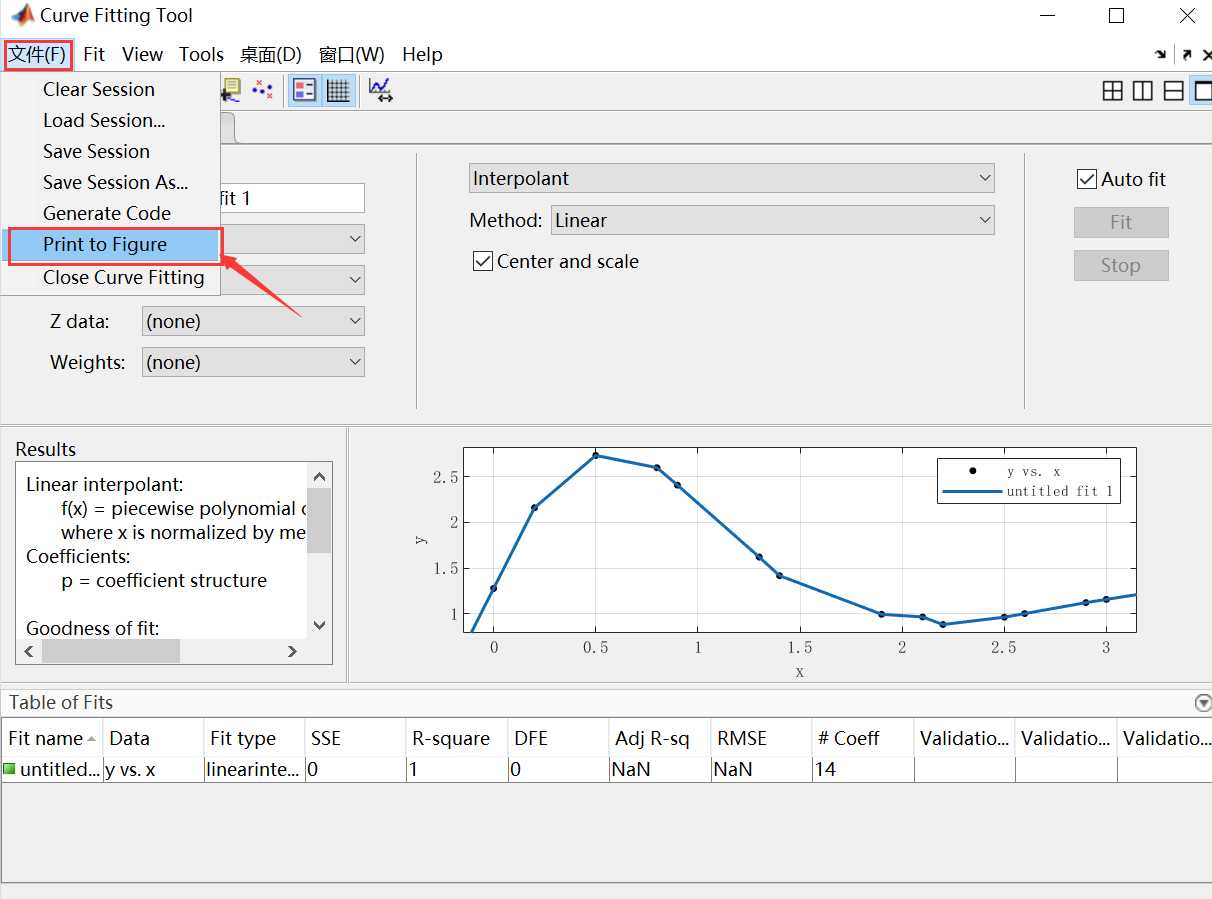
9.输出拟合参数

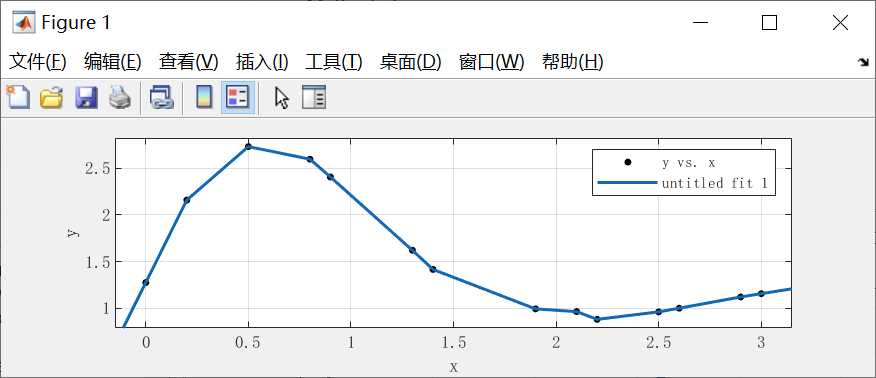
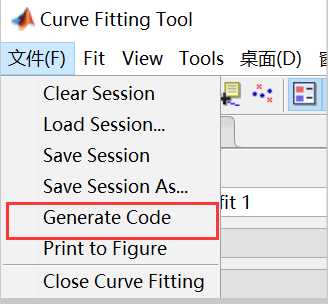
如果希望只显示拟合图像，可以点击“文件”——>“Print to figure”

这样就可以只显示拟合图像了，如下图所示。

如果希望导出拟合后的曲线数据，可以点击“文件”——>“Generate Code”

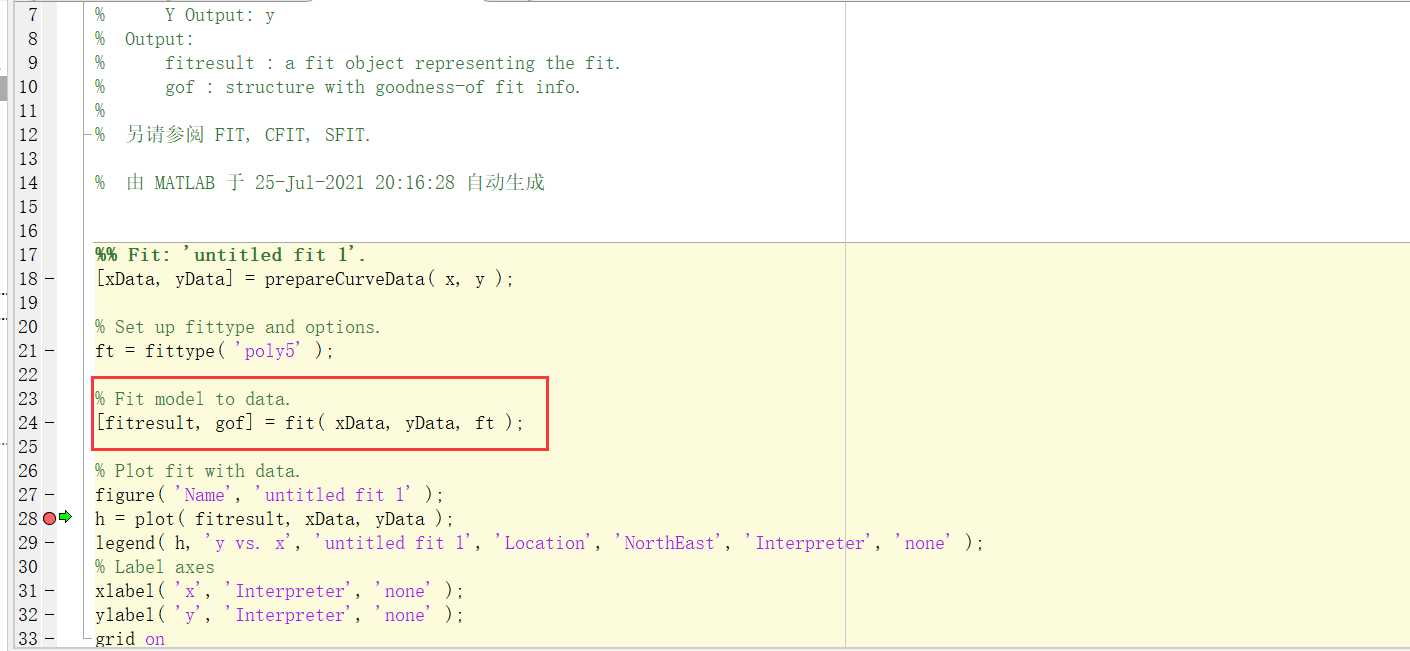
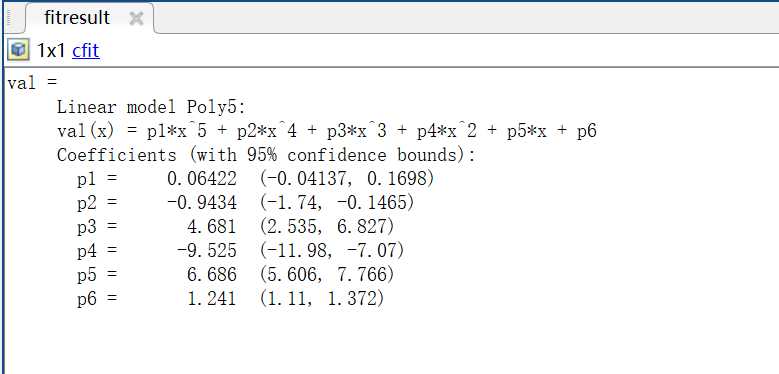
生成代码后，默认函数名为createFit，可以自行修改，直接保存，就可以调用了。比如说，我要导出五次多项式Polynomial逼近结果，按照上述方式导出后，可以查看生成代码的信息：

其中，fitresult是函数的输出，是一个结构体，可以用fitresult.p1得到p1的系数，同理其它系数也可得。

如果想导出拟合后的曲线数据，只需要把横坐标传给fitresult就可以了：

y = fitresult(x)';

10.结论

本文主要讨论了MATLAB曲线拟合工具箱（cftool）的拟合过程。通过工具箱模块可以非常方便地对曲线进行拟合，不需要太多的编程，曲线拟合方法多样，效果较好。

ok，以上便是曲线拟合工具箱的全部内容了，如果对你有所帮助，记得点个赞哟~