当遇到指标众多的场景时，以前通常的处理方法基本采用逐步回归的思想。即判断各指标之间的相关程度，保留几个重要的指标， 剔除其它不重要的指标。相关方法有：三大相关系数计算法、多元线性回归法、随机森林法、灰色相关系数法等。

此篇文章将介绍主成分分析，在不剔除任何指标的情况下实现数据的降维。

主成分分析简介

主成分分析是一种降维算法，它能将多个指标转换为少数几个主成分，这些主成分是原始变量的线性组合，且彼此之间互不相关，其能反映出原始数据的大部分信息。一般来说，当研究的问题涉及到多变量且变量之间存在很强的相关性时，我们可考虑使用主成分分析的方法来对数据进行简化。

主成分分析的思想

主成分分析计算步骤

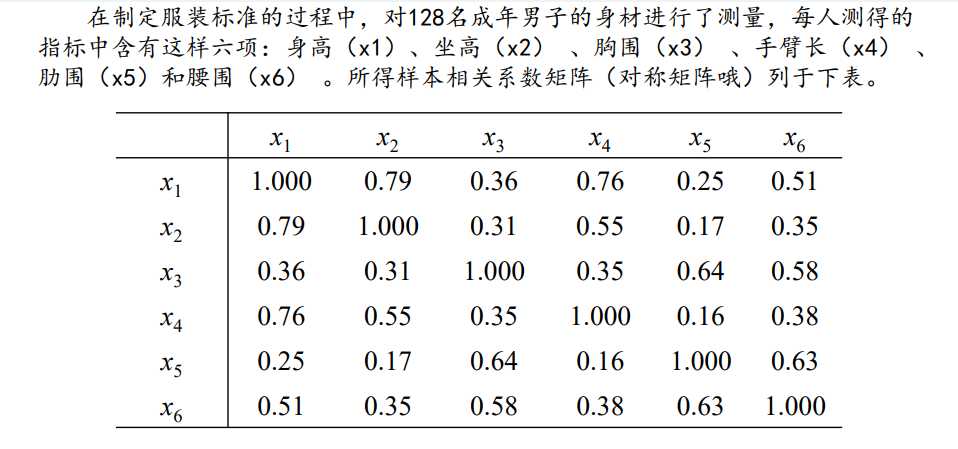
主成分分析指标解释案例

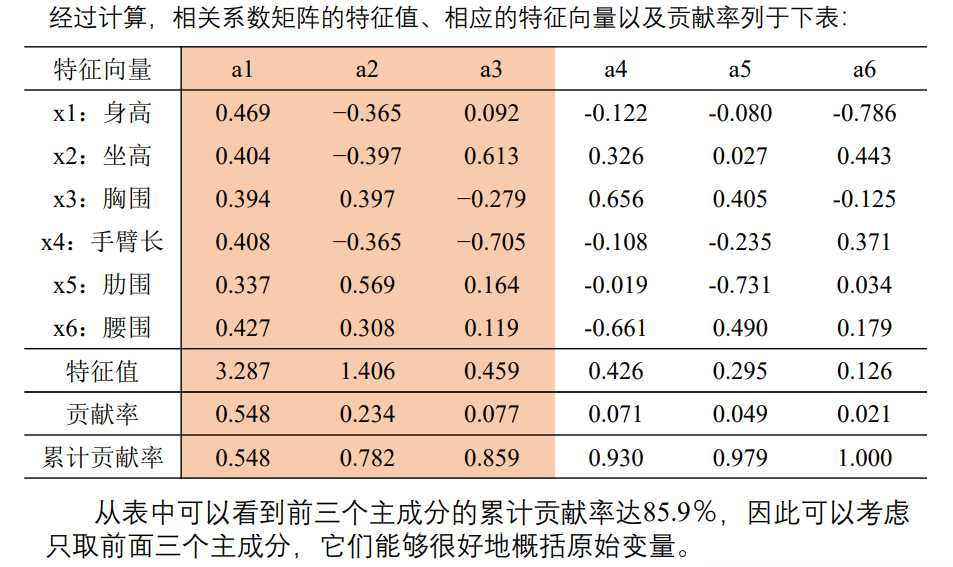
主成分分析的一大难点是指标意义模糊，难以解释，下面这个例子可以辅助理解。


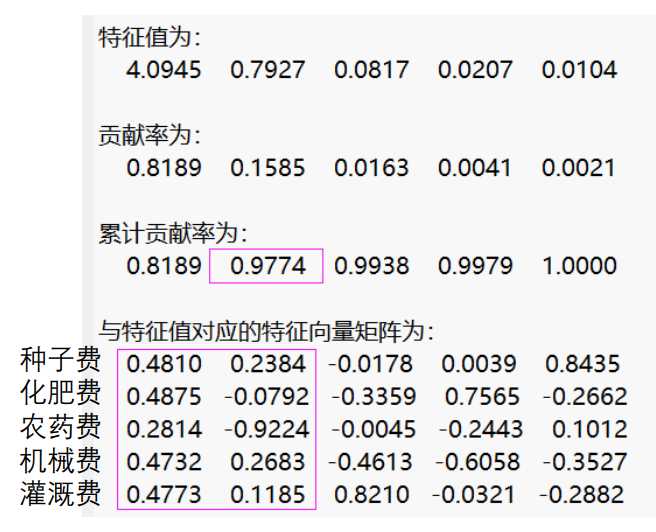
上表的累计贡献率 = 当前项贡献率 + 之前的累计贡献率。当累计贡献率 > 80%时，剩下的特征向量可以舍弃。

上面的分析需要一定的语言组织能力，也需要一定运气成分，若难以解释，或者强行解释，或者换方法。

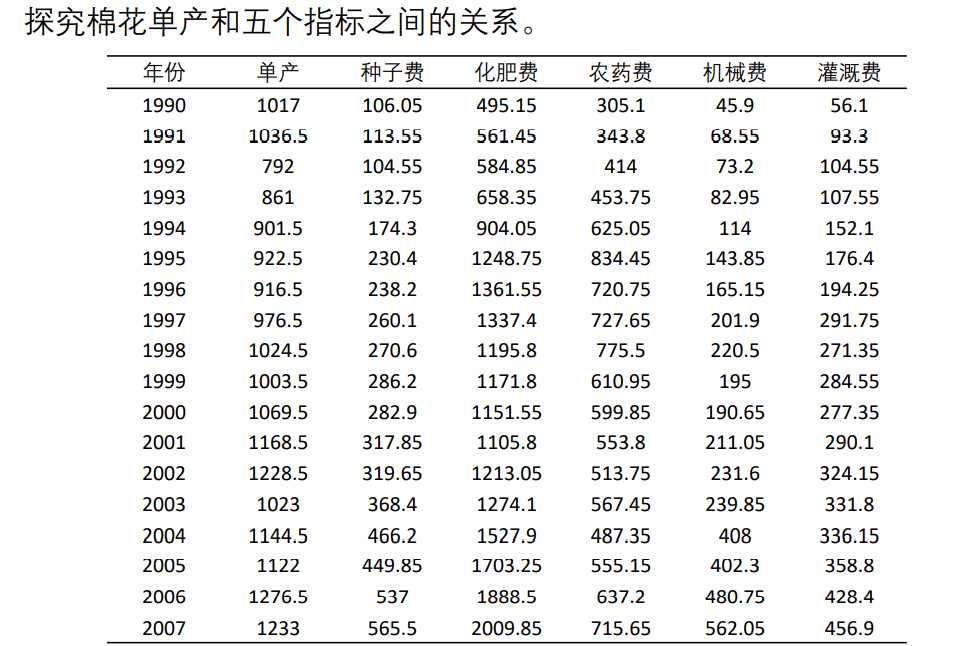
主成分分析matlab实操

下面给出一道例题：

加载数据：

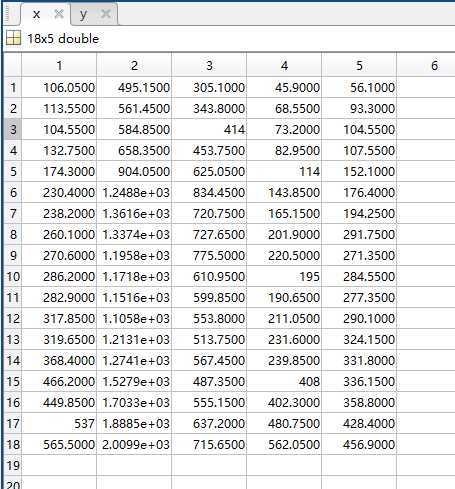
load data2.mat 

运行下面的代码，得到结果：

clear;clc
% load data1.mat   % 主成分聚类
load data2.mat   % 主成分回归

[n,p] = size(x);  % n是样本个数，p是指标个数

%% 第一步：对数据x标准化为X
X=zscore(x);   % matlab内置的标准化函数（x-mean(x)）/std(x)

%% 第二步：计算样本协方差矩阵
R = cov(X);

%% 注意：以上两步可合并为下面一步：直接计算样本相关系数矩阵
R = corrcoef(x);
disp('样本相关系数矩阵为：')
disp(R)

%% 第三步：计算R的特征值和特征向量
% 注意：R是半正定矩阵，所以其特征值不为负数
% R同时是对称矩阵，Matlab计算对称矩阵时，会将特征值按照从小到大排列哦
% eig函数的详解见第一讲层次分析法的视频
[V,D] = eig(R);  % V 特征向量矩阵  D 特征值构成的对角矩阵


%% 第四步：计算主成分贡献率和累计贡献率
lambda = diag(D);  % diag函数用于得到一个矩阵的主对角线元素值(返回的是列向量)
lambda = lambda(end:-1:1);  % 因为lambda向量是从小大到排序的，我们将其调个头
contribution_rate = lambda / sum(lambda);  % 计算贡献率
cum_contribution_rate = cumsum(lambda)/ sum(lambda);   % 计算累计贡献率  cumsum是求累加值的函数
disp('特征值为：')
disp(lambda')  % 转置为行向量，方便展示
disp('贡献率为：')
disp(contribution_rate')
disp('累计贡献率为：')
disp(cum_contribution_rate')
disp('与特征值对应的特征向量矩阵为：')
% 注意：这里的特征向量要和特征值一一对应，之前特征值相当于颠倒过来了，因此特征向量的各列需要颠倒过来
%  rot90函数可以使一个矩阵逆时针旋转90度，然后再转置，就可以实现将矩阵的列颠倒的效果
V=rot90(V)';
disp(V)


%% 计算我们所需要的主成分的值
m =input('请输入需要保存的主成分的个数: ');
F = zeros(n,m);  %初始化保存主成分的矩阵（每一列是一个主成分）
for i = 1:m
   ai = V(:,i)';   % 将第i个特征向量取出，并转置为行向量
   Ai = repmat(ai,n,1);   % 将这个行向量重复n次，构成一个n*p的矩阵
   F(:, i) = sum(Ai .* X, 2);  % 注意，对标准化的数据求了权重后要计算每一行的和
end

前两个的主成分累计贡献率已达97.74%，因此保存主成分的个数选择2。

输入个数之后，得到F矩阵，将数据导入Spss或Stata可以做聚类或回归。

%% (1)主成分聚类 ： 将主成分指标所在的F矩阵复制到Excel表格，然后再用Spss进行聚类
% 在Excel第一行输入指标名称（F1,F2, ..., Fm）
% 双击Matlab工作区的F,进入变量编辑中，然后复制里面的数据到Excel表格
% 导出数据之后，我们后续的分析就可以在Spss中进行。

%%（2）主成分回归：将x使用主成分得到主成分指标，并将y标准化，接着导出到Excel，然后再使用Stata回归
% Y = zscore(y);  % 一定要将y进行标准化哦~
% 在Excel第一行输入指标名称（Y,F1, F2, ..., Fm）
% 分别双击Matlab工作区的Y和F,进入变量编辑中，然后复制里面的数据到Excel表格
% 导出数据之后，我们后续的分析就可以在Stata中进行。