什么是回归分析?
回归分析是研究自变量与因变量之间数量变化关系的一种分析方法,它主要是通过因变量Y与影响它的自变量Xi(i1,2,3…)之间的回归模型,衡量自变量Xi对因变量Y的影响能力的,进而可以用来预测因变量Y的发展趋势。
🎈🎈🎈相关分析与回归分析的联系与区别:
- 联系:
两者均为研究与测度两个或两个以上变量之间关系的方法。
在实际工作中,一般先进行相关分析,计算相关函数,然后建立回归模型,最后用回归模型进行推算或预测。 - 区别:
✨相关分析研究的都是随机变量,并且不分自变量与因变量;
✨回归分析研究的变量要定义出自变量与因变量,并且自变量是确定的普通变量,因变量是随机变量;
✨相关分析描述的是两个变量之间相关关系的密切程度;
✨回归分析不仅可以揭示变量X对变量Y的影响程度,还可以根据回归模型进行预测。
回归分析包括:线性回归和非线性回归。
线性回归又分为:简单线性回归、多重线性回归。
非线性回归,需要通过对数转化等方式,将其转化为线性回归的形式进行研究。
线性回归分析步骤
回归分析五步法:
1、根据预测目标,确定自变量和因变量;
2、绘制散点图,确定回归模型类型;
3、估计模型参数,建立回归模型; (最小二乘法)
4、对回归模型进行检验;
5、利用回归模型进行预测。
简单线性回归和多重线性回归的区别:变量个数的不同。
简单线性回归
简单线性回归也称为一元线性回归,回归模型中只含有一个自变量,主要用来处理一个自变量与一个因变量之间的线性关系。
Y = a + bX + ε
Y:因变量
a:常熟项,是回归直线在纵坐标轴上的截距
b:回归系数,回归直线的斜率,表示自变量对因变量的影响程度
X:自变量
ε:随机差数,随机因素对因变量产生的因素
如何的到最佳的a和b,使得尽可能多的到(Xi,Yi)数据点落在或者更靠近这条拟合出来的直线上,最小二乘法就是一个较好的计算方法。
那么什么是最小二乘法呢?
最小二乘法,又称为最小平方法,通过最小化误差的平方和寻找数据的最佳函数匹配。
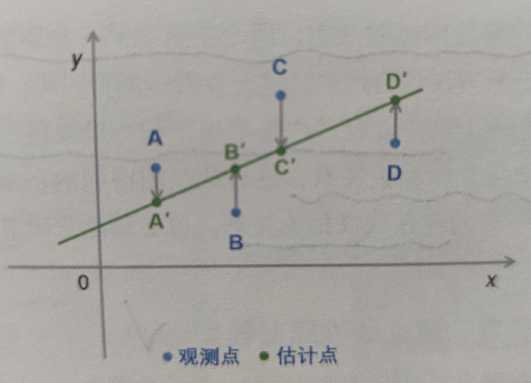
最小二乘法在回归模型上的应用,就是要使得观测点和估计点的距离的平方和达到最小。
“最小”指的是参数的估计值要保证各个观测点与估计点的距离的平方和达到最小,也就是刚才所说的使得尽可能多的(Xi,Yi)数据点落在或者更靠近这条拟合出来的直线上。
示例
了解投入不同的广告费用能带来多少销售额?
根据回归分析五步法:
🎀1、确定自变量和因变量
要预测广告费用的投入对销售额的影响,目标是预测销售额,所以将“广告费用”作为自变量,将“销售额”作为因变量,评估广告对销售的具体影响。
🎀2、绘制散点图
在进行回归分析前,我们先要了解自变量和因变量之间的相关关系,以便判断后续采取回归模型的类型。之前相关分析中有说道怎么绘制散点图。相关分析
根据之前相关分析可知,这两个变量之间存在着明显的线性关系;
“广告费用”和“销售额”之间皮尔逊相关系数 r = 0.816,为高度正相关关系,存在线性相关关系,可以尝试建立简单线性回归模型来预测销售额。
🎀3、估计模型参数,建立线性回归模型
SPSS中,【分析】——【回归】——【线性】——【线性回归】
设置自变量与因变量:
销售额->>>因变量
广告费用->>>自变量
方法(M)->>> 选择默认的输入
回归系数及拟合度设置:
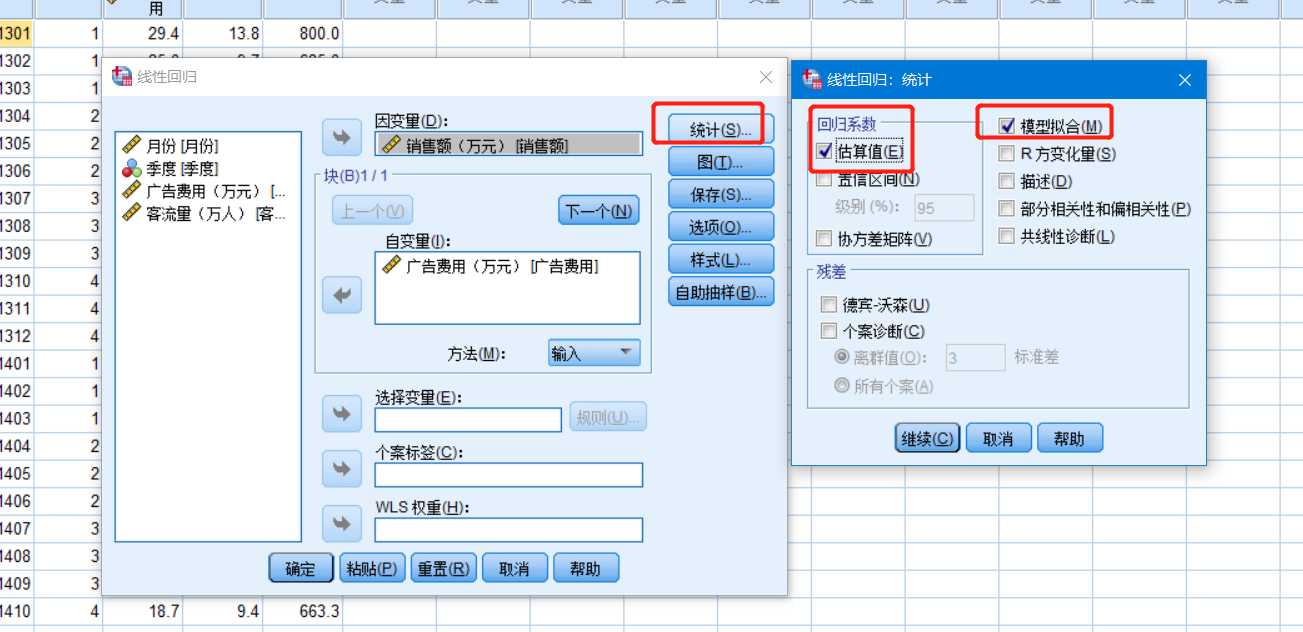
【统计】——【线性回归:统计】
一般情况下,设置两个参数,①勾选【回归系数】框中的【估算值】复选框,作用是估计出回归系数;②勾选【模型拟合】复选框,作用是输出判定系数 R²。其他选项保持默认设置即可,单击【继续】——【线性回归】
自变量步进及常数项设置:
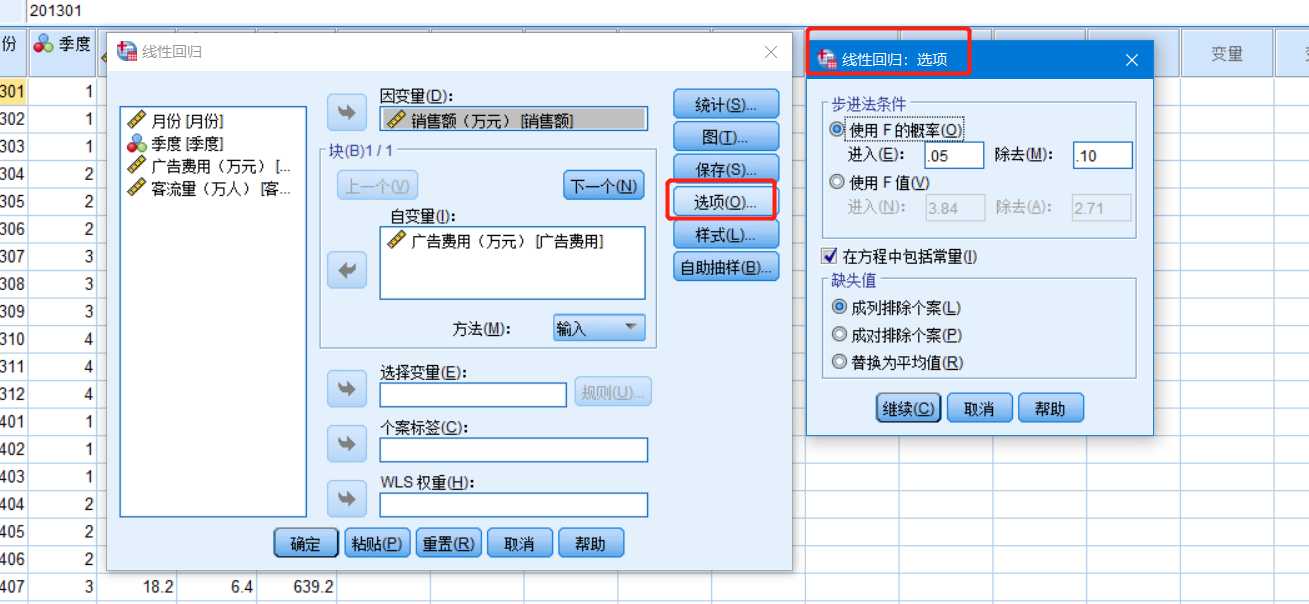
【线性回归】——【选项】——【线性回归:选型】
勾选【在方程中包括常量】,即输出拟合直线的截距a,其他保持默认。【继续】——返回【线性回归】——【确定】
🎀4、对回归模型进行检验
完成上述操作后,SPSS会输出4个结果表:
(1)线性回归模型输入/除去变量表😋
图中信息:自变量:广告费用,方法:输入,因变量:销售额。
(2)线性回归模型汇总表😋
R:0.816,销售额与广告费用为高度正相关关系。
R方:判定系数 R²,也称为拟合优度或决定系数,即相关系数R的平方,用于表示拟合得到的模型能解释因变量变化的百分比,R² 越接近1,表示回归模型拟合效果越好,R² = 0.666,模型效果一般,可以接受。
调整后R方:用于修正自变量个数的增加而导致模型拟合效果过高的情况,多用于衡量多重性回归分析模型的拟合效果。
标准估算的错误:大小反映了建立的模型预测因变量时的精度,在对比多个回归模型的拟合效果时,通常会比较该指标,调整后的R方越小,说明拟合效果越好。
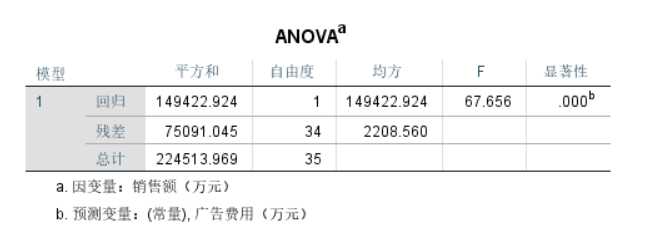
(3)线性回归方差分析表😋
方差分析表作用:
通过F检验来判断回归模型的回归效果,即检验因变量与所有自变量之间的线性关系是否显著。
表中有:平方和(SS)、自由度(df)、均方(MS)、F(F统计量)、显著性(P值)五大指标。
通过我们只需关注F和显著性两个指标,其中主要参考显著性,因为计算出F统计量,还需要查找统计表(F分布临界值表),并与之进行比较大小才能得出结果,而显著性P 可直接与显著性水平α(0.01、0.05)比较得出结果。
从图中我们可以看到,显著性(P值)=0.000<0.01,即认为模型1在0.01显著性水平下,由自变量广告费用和因变量销售额建立起来的线性关系具有极其显著的统计学意义。
显著性(P值)是在显著性水平α(常用取值0.01或0.05)下F的临界值,一般我们以此来衡量检验结果是否具有显著性;
🐾🐾🐾
显著性(P值)>0.05,不具有统计学意义;
0.01< 显著性(P值)<= 0.05,具有显著性统计学意义;
显著性(P值)<= 0.01,具有极其显著的统计学意义。
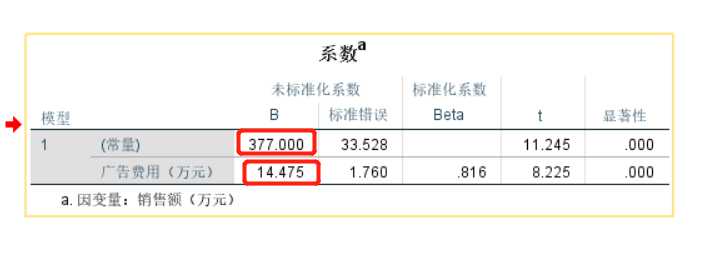
(4)线性回归模型回归系数表😋
B列:
377.000——代表常量 a(截距);
14.475——回归系数 b(斜率);
我们可以写出简单的线性回归模型:Y=377+14.475X
显著性(P)值:0.000<0.01,说明具有极其显著的统计学意义,即因变量销售额和自变量广告费用之间存在极其显著的线性关系。
标准化系数:用来测量自变量对因变量的重要性,只有将因变量和自变量标准化到统一的量纲下才能进行重要性的比较和衡量;图中标准化系数为0.816,与相关系数结果是一致的。
🎀5、利用回归模型进行预测
知道了简单的回归方程式,我们可以对因变量进行预测了:
假设下个月我们要投入20万元的广告费用,在其他因素都稳定的情况下,下个月的销售额预计是多少呢?代入公式:
Y=377+14.475X ——Y=377+14.475*20=666.5
也就是说,在下个月投入20万元广告费用的情况下,超市销售额预计可达到666.5万元左右。
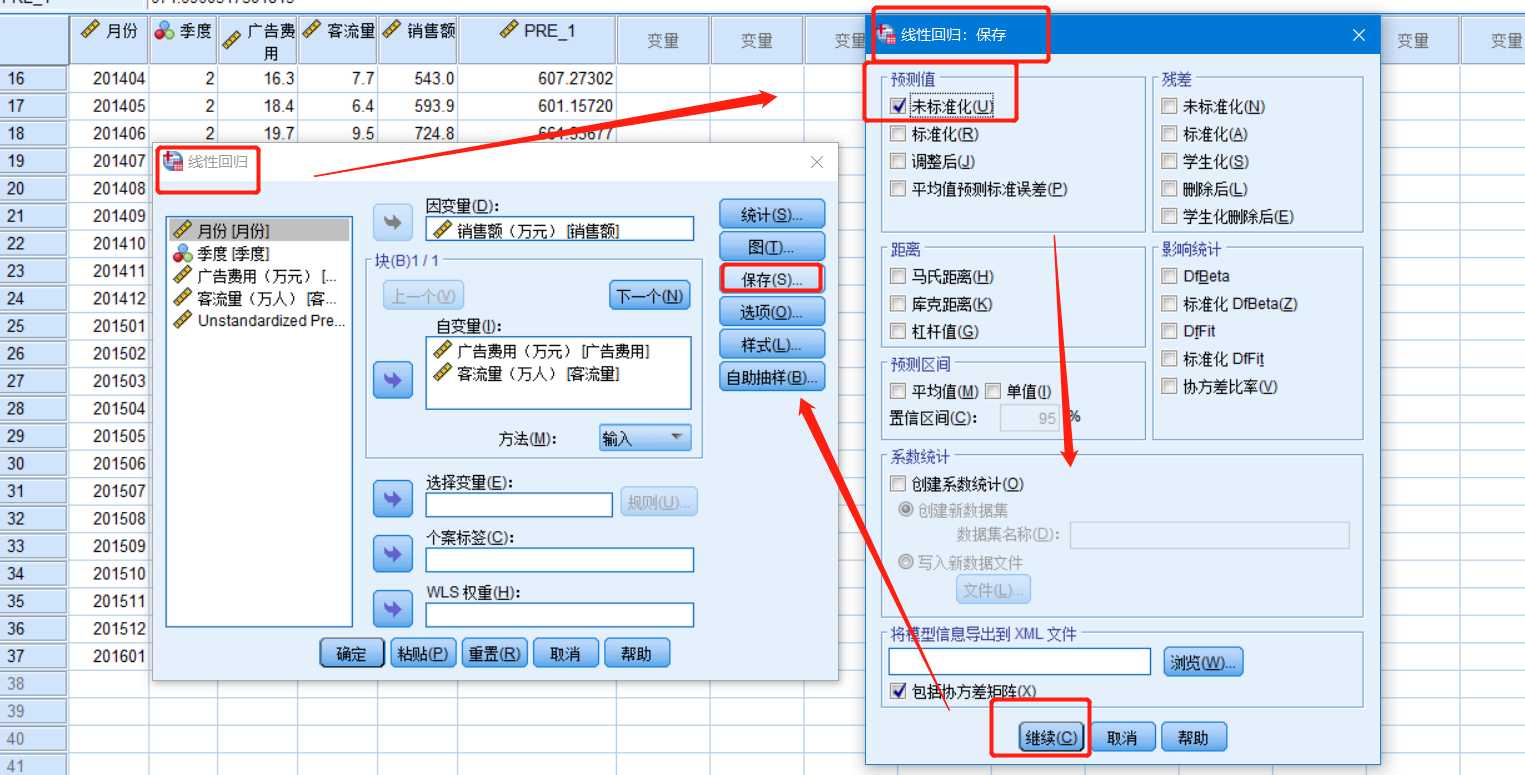
如果需要预测的数据较多时,我们可以利用SPSS来做。
【线性回归】——【保存】——【线性回归:保存】——【预测值】——【未标准化】——【继续】——【线性回归】——【确定】
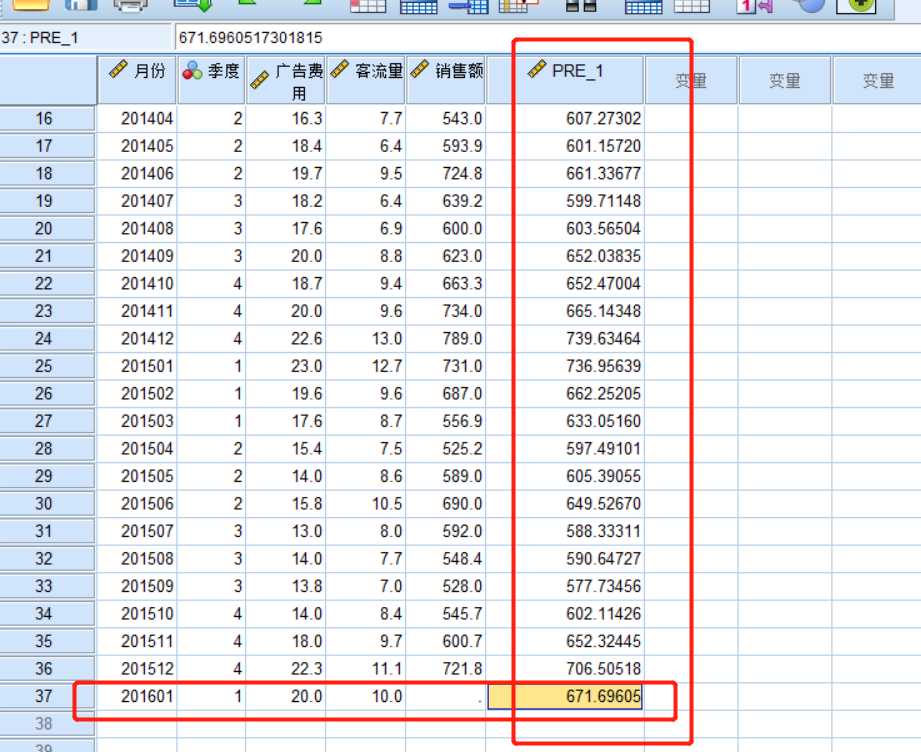
按照以上步骤 就得到了新增自变量对应的因变量预测值。
学习来源:《谁说菜鸟不会数据分析-SPSS篇》
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/34817.html