树同构判定

树同构判定

图同构与树同构

同的同构问题还没有有效算法。

树的同构本质上寻找不同树之间的双射关系。

通过对树编码，将树的同构问题转化为编码比较问题。

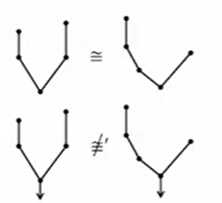
有根树的同构严格强于图同构关系。

如上，图同构的两张图转化成树，如果选取的根不同，则树不同构。

如何选取根？

概念定义：

1. dis(v1, v2)表示v1到v2点的距离

2. ex(v), 偏心率， ex(v)保存树中距离v最远的点的距离。

   ex(v1) = max(dis(v1, vk)) , k = 1 → n

3. C(T), 成为中心，表示图中偏心率最小的点集合。

   一种重要性质

   对于一个树来说(对于图不成立)，他的中心最多含有两个点，且若含有两个点，这两个点必定相邻。

所以，寻找一个树的中心，只需要迭代地删掉叶子节点，最后剩下的单个节点或者两个节点就是树的中心。

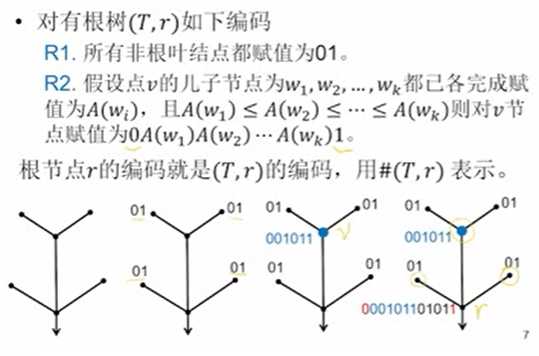
树的编码（有根树的同构判定）

将树转换字符串，但是通过比较字符串的字典序来比较两个编码的大小关系。

字典序比较规则：

编码方法

采用如上编码方案，两个树只有编码相同的时候才会同构。

reference

https://zh.coursera.org/lecture/discrete-mathematics-ch/you-gen-shu-tong-gou-de-pan-ding-NAxTd