树的同构

来自大佬的文章：树的同构
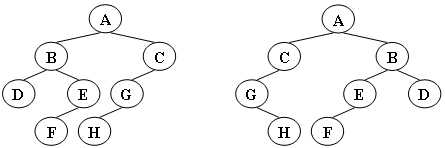
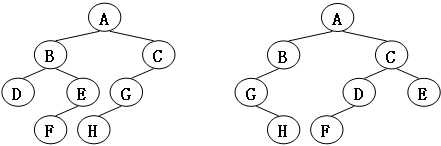
给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2，则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的，因为我们把其中一棵树的结点A、B、G的左右孩子互换后，就得到另外一棵树。而图2就不是同构的。

现给定两棵树，请你判断它们是否是同构的。
输入格式:

输入给出2棵二叉树树的信息。对于每棵树，首先在一行中给出一个非负整数NN (\le 10≤10)，即该树的结点数（此时假设结点从0到N-1N−1编号）；随后NN行，第ii行对应编号第ii个结点，给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空，则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意：题目保证每个结点中存储的字母是不同的。

输出格式:

如果两棵树是同构的，输出“Yes”，否则输出“No”。

输入样例1（对应图1）：

8
A 1 2
B 3 4
C 5 –
D – –
E 6 –
G 7 –
F – –
H – –
8
G – 4
B 7 6
F – –
A 5 1
H – –
C 0 –
D – –
E 2 –
输出样例1:

Yes
输入样例2（对应图2）：

8
B 5 7
F – –
A 0 3
C 6 –
H – –
D – –
G 4 –
E 1 –
8
D 6 –
B 5 –
E – –
H – –
C 0 2
G – 3
F – –
A 1 4
输出样例2:

No
————————————————

#include<cstdio>
#define MaxTree 10
#define Null -1
#include<stdio.h>
#define MaxTree 10
#define Null -1 //将Null定义为-1而不能是0，因为数组下标为0的地方仍保存有节点
typedef char ElementType;
typedef int Tree;
struct TreeNode{ 
       //定义二叉树节点
    ElementType Data;
    Tree Left;
    Tree Right;
}T1[MaxTree],T2[MaxTree];
int N,check[MaxTree];   //check数组用于寻找树的根节点
Tree BuildTree(struct TreeNode T[]){ 
   
    int Root=Null,i;    //刚开始将节点置为空，若为空树的时候可返回Null
    char cl,cr;
    scanf("%d",&N);
    if(N){ 
                 //如果不为空树的话
        for(i=0;i<N;i++) check[i]=0;    //将check数组置为0
        for(i=0;i<N;i++){ 
   
            scanf("\n%c %c %c",&T[i].Data,&cl,&cr); //把换行符放在前面吃掉前面scanf后的回车，而最后一个scanf不能有回车，一举两得
            if(cl!='-'){ 
   
                T[i].Left=cl-'0';
                check[T[i].Left]=1;
            }
            else
                T[i].Left=Null;
            if(cr!='-'){ 
   
                T[i].Right=cr-'0';
                check[T[i].Right]=1;
            }
            else
                T[i].Right=Null;
        }
        for(i=0;i<N;i++)
            if(!check[i])   break;
        Root=i;
    }
    return Root;
}
int Isomorphic(Tree R1,Tree R2){ 
   
    if((R1==Null)&&(R2==Null))      //如果为空树则是同构的
        return 1;
    if(((R1==Null)&&(R2!=Null))||((R1!=Null)&&(R2==Null)))//如果一个为空一个不为空则不是同构的
        return 0;
    if((T1[R1].Data)!=(T2[R2].Data))//如果数据不同则不是同构的
        return 0;
    //如果左儿子都为空判断右儿子是否同构：主要看以上三个方面（1）右儿子是否都为空（2）是否一个有右儿子一个没有（3）右儿子数据是否相同
    if((T1[R1].Left==Null)&&(T2[R2].Left==Null))
        return Isomorphic(T1[R1].Right,T2[R2].Right);
    /* 如果两棵树左儿子都不为空并且数据还是一样的，对左儿子进行递归*/
    if ( ((T1[R1].Left!=Null)&&(T2[R2].Left!=Null))&&((T1[T1[R1].Left].Data)==(T2[T2[R2].Left].Data)) )
        return ( Isomorphic( T1[R1].Left, T2[R2].Left )&&Isomorphic( T1[R1].Right, T2[R2].Right ) );
    /* 如果两棵树左儿子（一个空一个不空或者都不空）并且数据不一样，那么判断第一棵树的左（右）儿子是否跟第二棵树的右（左）儿子同构 */
    else
        return ( Isomorphic( T1[R1].Left, T2[R2].Right)&&Isomorphic( T1[R1].Right, T2[R2].Left ) );

}
int main(){ 
   
    Tree R1,R2;     //首先建立两棵树，R1，R2为树的根节点
    R1=BuildTree(T1);
    R2=BuildTree(T2);
    if(Isomorphic(R1,R2))   //Isomorphic函数判断是否同构
        printf("Yes\n");
    else printf("No\n");
    return 0;
}

树的同构就是熟悉一下树的表示方法，其实树的同构就是判断两个树是否翻转相等，从节点本身和节点的各个属性来判断，学习树的同构就是用来学习和熟悉一下树的属性和它的线性表示方法
表示的方法就是将各个节点的属性输出：
1.内容
2.左子节点和右子节点的线性位置
如果没有左子节点和右子节点那么用-1表示其位置。
用来查询哪个点是头结点的方式是从0位置开始遍历，如果哪个位置没有被
用过那么就是哪个位置为头节点，再有就是输入时要转换一下。
然后就是同构：
先寻找一个子模型
再去不断去递归寻找判断每一个子模型，输出。
情况稍多，自己看代码。
用静态链表的方式也就是数组存储树简单一点
本文最早来源于浙江大学的课件和mooc课程。