哈希算法在判定树同构方面的应用（下）

哈希算法在判定树同构方面的应用

在上一篇文章中我们介绍了 枚举根节点哈希 和 求重心哈希 两种方法来判断两棵无根树是否同构。

但是如果有些题目中我必须要计算出每个根节点的 $f$ 值，且 $n\le 1e5$ ，我们要怎么办呢？

考虑以下问题。

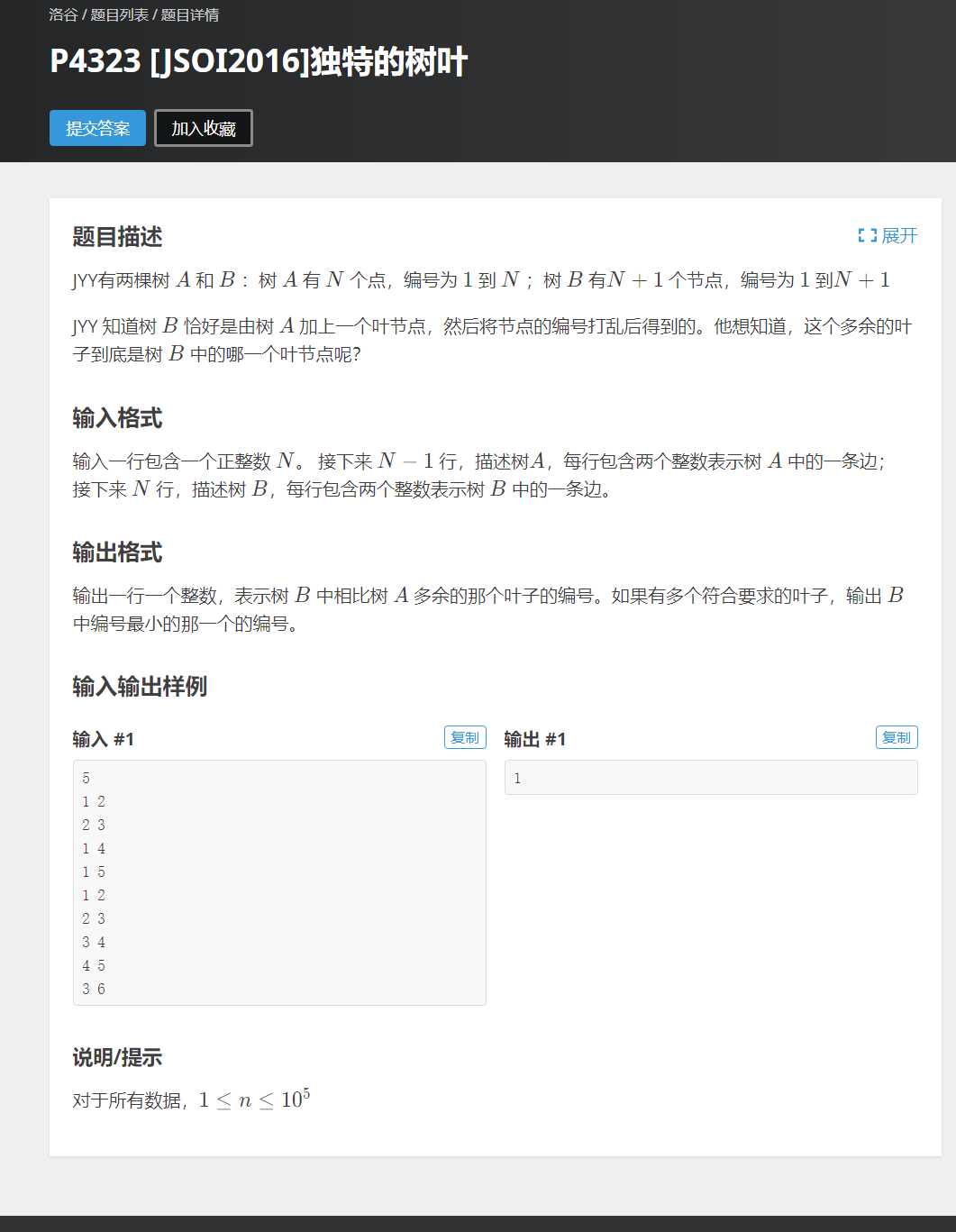
（一）：洛谷–P4323 [JSOI2016]独特的树叶

题解：
考虑如下解法。

我们求解 $A$ 树中，以每一点 $x$ 为根的 $f [x]$ 值并保存。

我们枚举 $B$ 树中的叶子节点，计算删去这个叶子节点后，这个叶子节点的父亲的 $f$ 值，即计算 $f [f a t h e r [当前叶子]]$ 。

如果在 $A$ 树的 $f [x]$ 中存在一个值与 $f [f a t h e r [当前叶子]]$ 相等，那就说明对于 $B$ 树中以某一点 $y$ 为根的 $f [y]$ ，在 $A$ 树中能找到一点 $x$ ，使得以 $x$ 为根的 $f [x] = f [y]$ 。那么 $A$ 树与 $B$ 树同构，当前叶子节点符合要求。

当前问题的关键点转化为怎么快速求出，无根树中，以任意一点 $x$ 为根的 $f [x]$

我们将当前无根树转化为根节点为 $1$ 的有根树。

对根节点 $1$ 进行求解，得到 $f [1]$ ，此时各点 $f [x]$ 表示整棵树以 $1$ 为根，且当前为节点 $x$ 子树的哈希值。

我们设一个辅助数组 $g [x]$ ，表示整棵树以 $x$ 为根的哈希值，初始时 $g [1] = f [1]$ 。

假设 $y\in son_x$ ，且当前 $g [x]$ 已求出，考虑怎么求解 $g [y]$ 。

我们已经求出 $f[y]=1+\sum\limits_{z\in son_y\space and\space z\neq x}f[z]*p[si[z]]$ ，我们要得到以 $y$ 为根的哈希值 $g [y]$ 。

$g [y] = f [y] +$ (以 $y$ 为根的树中，子树 $x$ 的哈希值) $* p [n - s i [y]]$ 。

其中 ( 以 $y$ 为根的树中，子树 $x$ 的哈希值 ) 等于 $(g [x] - f [y] * p [s i [y]])$ 。

$n - s i [y]$ 为以 $y$ 为根时， $x$ 子树的大小。

其中 $n$ 为这棵树的大小。

即 $g [y] = f [y] + (g [x] - f [y] * p [s i [y]]) * p [(n - s i [y])]$ ，那么我们再进行一遍 $d f s$ 即可以求出 $g [x]$ 。
$g [x]$ 为以 $x$ 为根的哈希值。

回到本题：
（1）求解 A 树的 $g [x]$ 并保存至 $s e t$ 中。
（2）求解 B 树的 $g [x]$
（3）枚举叶子节点，检查去掉叶子节点后 $B$ 树与 $A$ 树是否同构。

空间复杂度 $O (n)$ ，时间复杂度 $O (n l o g n)$ ， $l o g n$ 是因为维护了 $s e t$ 。

代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<string>
#include<vector>
#include<map>
#include<set>
#include<cmath>
#include<queue>
#define ll long long
#define llu unsigned ll
#define pr make_pair
#define pb push_back
#define lc (cnt<<1)
#define rc (cnt<<1|1)
using namespace std;
const int inf=0x3f3f3f3f;
const ll lnf=0x3f3f3f3f3f3f3f3f;
const double dnf=1e15;
const int mod=1e9+7;
const int maxn=1000100;
int head[maxn],ver[maxn],nt[maxn],d[maxn];
int fa[maxn],si[maxn],tot=1,n;
llu g[maxn],f[maxn];
int p[maxn<<1],cnt=0;
bool ha[maxn<<1];
set<llu> se;

//素数筛，可以先打表看一下，素数筛的上界
void prime(void)
{ 
   
    ha[1]=true;
    for(int i=2;i<(maxn<<1);i++)
    { 
   
        if(!ha[i]) p[++cnt]=i;
        for(int j=1;j<=cnt&&i*p[j]<(maxn<<1);j++)
        { 
   
            ha[i*p[j]]=true;
            if(i%p[j]==0) break;
        }
    }
}

//初始化存图
void init(void)
{ 
   
    memset(head,0,sizeof(head));
    tot=1;
    n++;
}

void add(int x,int y)
{ 
   
    ver[++tot]=y,nt[tot]=head[x],head[x]=tot;
}

//处理f[x]
void dfs1(int x,int ff)
{ 
   
    f[x]=si[x]=1;
    for(int i=head[x];i;i=nt[i])
    { 
   
        int y=ver[i];
        if(y==ff) continue;
        dfs1(y,x);
        f[x]+=f[y]*p[si[y]];
        si[x]+=si[y];
    }
}

//求解 g[x],g[x]为以x为根的哈希值
void dfs2(int x,int ff)
{ 
   
    for(int i=head[x];i;i=nt[i])
    { 
   
        int y=ver[i];
        if(y==ff) continue;
        g[y]=f[y]+(g[x]-f[y]*p[si[y]])*p[n-si[y]];
        dfs2(y,x);
    }
}


int main(void)
{ 
   
    prime();
    scanf("%d",&n);
    int x,y;
    for(int i=1;i<n;i++)
    { 
   
        scanf("%d%d",&x,&y);
        add(x,y);
        add(y,x);
    }
    dfs1(1,0);
    g[1]=f[1];
    dfs2(1,0);
    //保存A树的
    for(int i=1;i<=n;i++)
        se.insert(g[i]);

    init();
    for(int i=1;i<n;i++)
    { 
   
        scanf("%d%d",&x,&y);
        d[x]++,d[y]++;
        add(x,y);
        add(y,x);
        fa[x]=y,fa[y]=x;//注意这里叶子节点怎么找它的上一节点
    }
    dfs1(1,0);
    g[1]=f[1];
    dfs2(1,0);
	
	//枚举叶子节点
    for(int i=1;i<=n;i++)
    { 
   
    	//g[fa[i]]-p[1]，因为叶子节点的大小一定为1，
    	//这个值就是去掉叶子节点后，以fa[i] 为根的树的哈希值。
        if(d[i]==1&&se.find(g[fa[i]]-p[1])!=se.end())
        { 
   
            printf("%d\n",i);
            break;
        }
    }

    return 0;
}

（二）综合练习：石油大–17102、Regular Forestation
这个 $O J$ 可能会上不去。
CF题目：CodeForces – 1252F

题面：

题意：
给定一棵无根树，如果去掉点 $x$ 且去掉与点 $x$ 相连的边，剩下的部分是由 $k$ 棵树组成的森林，且这 $k$ 棵树同构，且 $k > 1$ 。那么称 $x$ 是一个好的切分点。

输出去掉某一个好的切分点后最大的 $k$ 。

题解：

数据量只有 $4000$ ，很容易想到解决方案可能是 $O(n^2)$ 复杂度的算法。

我们枚举每个点 $x$ ，判定这个点是否是好的切分点，同时用 $k$ 更新答案。

在判断两棵树是否同构的时候，我们需要求出这两棵无根子树以每个点为根的哈希值，然后将这两个哈希值序列进行排序，如果两棵无根子树排序后的哈希值序列完全一样，那么这两棵树同构（因为如果两棵无根树同构，那么在 $A$ 树中若以某一点 $x$ 为根，那么在树 $B$ 中总能找到一点 $y$ ，使得以 $x, y$ 为根的树同构）。这个时间复杂度是 $O (n l o g n)$ 的，求一棵树每个点为根的哈希值是 $O (n)$ 的，但是排序是 $O (n l o g n)$ 的。

再套上外层的 $O (n)$ ，那么时间复杂度是 $O(n^2logn)$ 的，显然不能通过此题。

考虑如何剪枝。

我们去掉一点 $x$ ，如果剩下的 $k$ 棵树同构，那么首先要要求剩下的 $k$ 棵树的大小一样。感性理解一下如果去掉一点 $x$ 能使剩下的 $k$ 棵树的大小一样，这样的点 $x$ 是不多的。（其实这样的点 $x$ 只能是重心且至多有一个，因为要去掉某一点后使得剩下的树的大小一样，如果重心不符合要求，那么其他点一定也不符合要求。因为在第一次写题的时候没考虑到这么多，所以将 $d f s$ 函数换成找重心也可以过）

找到重心（或者找到删除该点后使得剩下的树大小一致的点），只需要判断这个点的所有子树是否同构即可。
时间复杂度 $O (n l o g n)$

代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<string>
#include<queue>
#include<bitset>
#include<map>
#include<unordered_map>
#include<unordered_set>
#include<set>
#include<ctime>
#define ui unsigned int
#define ll long long
#define llu unsigned ll
#define ld long double
#define pr make_pair
#define pb push_back
#define lc (cnt<<1)
#define rc (cnt<<1|1)
#define len(x) (t[(x)].r-t[(x)].l+1)
#define tmid ((l+r)>>1)
#define fhead(x) for(int i=head[(x)];i;i=nt[i])
#define max(x,y) ((x)>(y)?(x):(y))
#define min(x,y) ((x)>(y)?(y):(x))
using namespace std;

const int inf=0x3f3f3f3f;
const ll lnf=0x3f3f3f3f3f3f3f3f;
const double dnf=1e18;
const double alpha=0.75;
const int mod=1e9+7;
const double eps=1e-8;
const double pi=acos(-1.0);
const int hp=13331;
const int maxn=100100;
const int maxm=100100;
const int maxp=100100;
const int up=1100;


int p[maxn],cnt=0;
bool ha[maxn];
void Prime(void)
{ 
   
    ha[1]=true;
    for(int i=2;i<maxn;i++)
    { 
   
        if(!ha[i]) p[++cnt]=i;
        for(int j=1;j<=cnt&&i*p[j]<maxn;j++)
        { 
   
            ha[i*p[j]]=true;
            if(i%p[j]==0) break;
        }
    }
}

int head[maxn],ver[maxn],nt[maxn],si[maxn],tot=1,n;
int d[maxn],maxx=-1,nowsi;
vector<pair<int,int> >ans;
llu f[maxn],g[maxn];
vector<llu>vc,vvc;

void add(int x,int y)
{ 
   
    ver[++tot]=y,nt[tot]=head[x],head[x]=tot;
}
//找某点被去点后剩下的子树大小相等的点
void dfs(int x,int fa)
{ 
   
    si[x]=1;
    vector<int>vc;
    vc.clear();
    for(int i=head[x];i;i=nt[i])
    { 
   
        if(ver[i]==fa) continue;
        dfs(ver[i],x);
        si[x]+=si[ver[i]];
        vc.pb(si[ver[i]]);
    }

    if(x!=1)
    	vc.pb(n-si[x]);
    if(vc.size()==1) return ;
    for(int i=1;i<vc.size();i++)
    { 
   
        if(vc[i]!=vc[i-1])
            return ;
    }
    ans.pb(pr(-vc.size(),x));
}

//计算f
void dfs1(int x,int fa)
{ 
   
    f[x]=si[x]=1;
    for(int i=head[x];i;i=nt[i])
    { 
   
        int y=ver[i];
        if(y==fa) continue;
        dfs1(y,x);
        f[x]+=f[y]*p[si[y]];
        si[x]+=si[y];
    }
}

//计算g
void dfs2(int x,int fa)
{ 
   
    vvc.pb(g[x]);
    for(int i=head[x];i;i=nt[i])
    { 
   
        int y=ver[i];
        if(y==fa) continue;
        g[y]=f[y]+(g[x]-f[y]*p[si[y]])*p[nowsi-si[y]];
        dfs2(y,x);
    }
}

void get(void)
{ 
   
    for(int k=0;k<ans.size();k++)
    { 
   
        if(-ans[k].first<=maxx) continue;
        int cnt=0,x=ans[k].second;
        bool flag=true;
        for(int i=head[x];i;i=nt[i])
        { 
   
            vvc.clear();
            cnt++;
            dfs1(ver[i],x);
            g[ver[i]]=f[ver[i]];
            nowsi=si[ver[i]];
            dfs2(ver[i],x);
            sort(vvc.begin(),vvc.end());
            if(cnt==1) vc=vvc;
            else if(vc!=vvc)
            { 
   
                flag=false;
                break;
            }
        }
        if(flag) maxx=max(maxx,cnt);
    }
}

int main(void)
{ 
   
    Prime();
    random_shuffle(p+1,p+cnt+1);
    int x,y;
    scanf("%d",&n);
    for(int i=1;i<n;i++)
    { 
   
        scanf("%d%d",&x,&y);
        add(x,y);
        add(y,x);
        d[x]++,d[y]++;
    }
    dfs(1,0);
    sort(ans.begin(),ans.end());
    get();
    printf("%d\n",maxx);
    return 0;
}

上述时间复杂度为 $O (n l o g n)$

考虑 $O (n)$ 的算法。

首先来复习一下树的重心的知识。

树的重心：找到一个点 $x$ , 以点 $x$ 为根时，其所有的子树中最大的子树节点数最少,那么这个点 $x$ 就是这棵树的重心。（以重心为根时，最大子树最小）

性质：
（1）树中所有点到某个点的距离和中，到重心的距离和是最小的，如果有两个重心，他们的距离和一样。
（2）把两棵树通过一条边相连，新的树的重心在原来两棵树重心的连线上。
（3）一棵树添加或者删除一个节点，树的重心最多只移动一条边的位置。
（4）一棵树最多有两个重心，且相邻。
（5）删除重心后所得的所有子树，节点数不超过原树的1/2。

那么我们可以得到，如果两棵无根树同构，那么他们的重心是一致的。
那么我们在判定两棵树是否同构时，可以先 $O (n)$ 求出两棵树的重心（可能有两个），然后再 $O (n)$ 判定两棵树是否同构即可。

时间复杂度： $O (n)$ 但是会带一个小常数，大约 $2 - 3$ 。

代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<string>
#include<queue>
#include<bitset>
#include<map>
#include<unordered_map>
#include<unordered_set>
#include<set>
#include<ctime>
#define ui unsigned int
#define ll long long
#define llu unsigned ll
#define ld long double
#define pr make_pair
#define pb push_back
#define lc (cnt<<1)
#define rc (cnt<<1|1)
#define len(x) (t[(x)].r-t[(x)].l+1)
#define tmid ((l+r)>>1)
#define fhead(x) for(int i=head[(x)];i;i=nt[i])
#define max(x,y) ((x)>(y)?(x):(y))
#define min(x,y) ((x)>(y)?(y):(x))
using namespace std;

const int inf=0x3f3f3f3f;
const ll lnf=0x3f3f3f3f3f3f3f3f;
const double dnf=1e18;
const double alpha=0.75;
const int mod=1e9+7;
const double eps=1e-8;
const double pi=acos(-1.0);
const int hp=13331;
const int maxn=100100;
const int maxm=100100;
const int maxp=100100;
const int up=1100;


int p[maxn],cnt=0;
bool ha[maxn];
void Prime(void)
{ 
   
    ha[1]=true;
    for(int i=2;i<maxn;i++)
    { 
   
        if(!ha[i]) p[++cnt]=i;
        for(int j=1;j<=cnt&&i*p[j]<maxn;j++)
        { 
   
            ha[i*p[j]]=true;
            if(i%p[j]==0) break;
        }
    }
}

int head[maxn],ver[maxn],nt[maxn],si[maxn],tot=1,n;
int d[maxn],ff[maxn],si1[maxn],dp[maxn],maxx=-1,nowsi,nowx;
int rt1,rt2;
vector<pair<int,int> >ans;
llu f[maxn];

void add(int x,int y)
{ 
   
    ver[++tot]=y,nt[tot]=head[x],head[x]=tot;
}

//找某点被删掉之后剩下的子树大小相等的点
void dfs(int x,int fa)
{ 
   
    si1[x]=1;
    vector<int>vc;
    vc.clear();
    for(int i=head[x];i;i=nt[i])
    { 
   
        if(ver[i]==fa) continue;
        ff[ver[i]]=x;
        dfs(ver[i],x);
        si1[x]+=si1[ver[i]];
        vc.pb(si1[ver[i]]);
    }

    if(x!=1)
    	vc.pb(n-si[x]);
    if(vc.size()==1) return ;
    for(int i=1;i<vc.size();i++)
    { 
   
        if(vc[i]!=vc[i-1])
            return ;
    }
    ans.pb(pr(-vc.size(),x));
}

//找重心
void dfs1(int x,int fa)
{ 
   
    si[x]=1,dp[x]=0;
    for(int i=head[x];i;i=nt[i])
    { 
   
        int y=ver[i];
        if(y==fa) continue;
        dfs1(y,x);
        si[x]+=si[y];
        dp[x]=max(dp[x],si[y]);
    }
    dp[x]=max(dp[x],nowsi-si[x]);
    if(rt1==0||dp[x]<dp[rt1]) rt1=x,rt2=0;
    else if(dp[x]==dp[rt1]) rt2=x;
}

//求f
void dfs2(int x,int fa)
{ 
   
    f[x]=si[x]=1;
    for(int i=head[x];i;i=nt[i])
    { 
   
        int y=ver[i];
        if(y==fa||y==nowx) continue;
        dfs2(y,x);
        f[x]+=f[y]*p[si[y]];
        si[x]+=si[y];
    }
}



void get(void)
{ 
   
    for(int k=0;k<ans.size();k++)
    { 
   
        if(-ans[k].first<=maxx) continue;
        int cnt=0,x=ans[k].second;
        bool flag=true;
        //虽然以下ans都初始化为0，有冲突的风险，但是这个风险还是比较小的。
        llu ans1=0,ans2=0;
        llu ansnow1=0,ansnow2=0;
        for(int i=head[x];i;i=nt[i])
        { 
   
            ansnow1=0,ansnow2=0;
            ++cnt;
            int y=ver[i];
            if(y==ff[x]) nowsi=n-si1[x];
            else nowsi=si1[y];
            rt1=0,rt2=0;
            dfs1(ver[i],x);

            nowx=x;
            if(rt1!=0) dfs2(rt1,0),ansnow1=f[rt1];
            if(rt2!=0) dfs2(rt2,0),ansnow2=f[rt2];

            if(cnt==1) ans1=ansnow1,ans2=ansnow2;
            else if(!((ans1==ansnow1&&ans2==ansnow2)||(ans1==ansnow2&&ans2==ansnow1)))
            { 
   
                flag=false;
                break;
            }
        }
        if(flag) maxx=max(maxx,cnt);
    }
}

int main(void)
{ 
   
    Prime();
    random_shuffle(p+1,p+cnt+1);
    int x,y;
    scanf("%d",&n);
    for(int i=1;i<n;i++)
    { 
   
        scanf("%d%d",&x,&y);
        add(x,y);
        add(y,x);
        d[x]++,d[y]++;
    }
    dfs(1,0);
    sort(ans.begin(),ans.end());
    get();
    printf("%d\n",maxx);
    return 0;
}

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容，请发送邮件至举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/35318.html

哈希算法在判定树同构方面的应用（下）

相关推荐

发表回复