一、matlab插值比较-griddata/interp2

最近在使用matlab插值，发现采用griddata计算速度太慢，正好是网格数据就将计算结果与interp2开展了对比，发现速度差别特别大。

%%
tic
FusioG = griddata(lon,lat,FusioGr,data(:,2),data(:,3));  
toc
disp(['运行时间: ',num2str(toc)]);


时间已过 16.637986 秒。
运行时间: 16.64

tic
FusioG1 = interp2(lon,lat,FusioGr,data(:,2),data(:,3)); 
toc
disp(['运行时间: ',num2str(toc)]);


时间已过 0.085138 秒。
运行时间: 0.085863

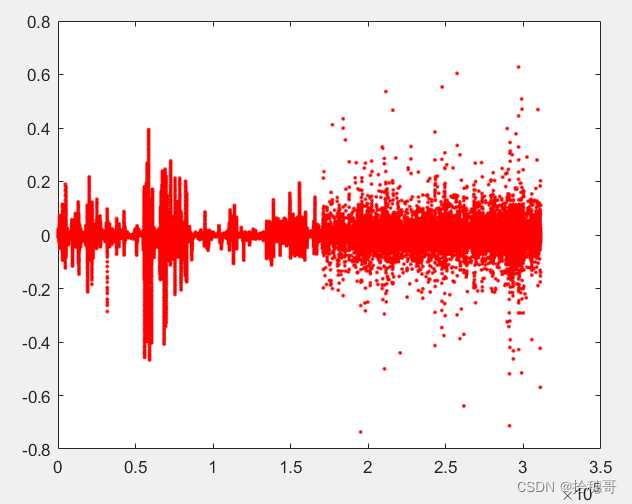
plot(FusioG - FusioG1 ,'r.')
A  = FusioG - FusioG1;

rms(A)

ans =

   NaN

mean(A)

ans =

   NaN

max(A)

ans =

    0.6278

 min(A)

ans =

   -0.7366

两种结果插值成图

通过对比，发现采用interp2插值时运算时间从griddata的16.64秒降为0.085863。

插值rms和mean均为NaN，主要是大部分的节点的值为0.000546720777908405附近，无法计算。

差值max= 0.6278；差值min = -0.7366，表明两者插值还是有些许的不同。插值结果对于总体量31万个点而言可以近似相等。

二维插值与MATLAB实例解析

二维插值-MATLAB_感谢地心引力的博客-CSDN博客_二维插值

百度安全验证   Matlab之插值函数汇总及使用说明

一、插值节点为网格节点
二、插值节点为散乱节点
Addition：
（1）学会查看matlab帮助文档
（2）matlab脚本类型
（3）matlab三维绘图函数
二维插值，简单来说就是节点二维、插值函数二维，形如z = f ( x , y ) z=f(x,y)z=f(x,y)。

  为什么要插值呢？假如我们要根据已知的二维数据来绘制对应的三维曲面图像，就需要很多点的x、y、z坐标，但给定的数据一般比较少，不能仅仅通过点数据画出三维图形。又或者要获取未知点的坐标值（大概的）。

一、插值节点为网格节点

 网格节点，听命字就知道它是比较规则整齐的点了。相当于在xyz平面内，一条条整齐的平行于x，y轴的直线相交，再在z轴方向对应一个值。

比如这样：

 MATLAB插值命令：

                                z=interp2(x0​,y0​,z0​,x,y,′method′)

其中:
x0，y0为已知节点,z是对应的值;
x0，y0分别为m维、n维向量，z为m·n矩阵;  
x，y是要插值的节点，z返回对应的插值得到的值;
method是插值方法，和一维插值相同:
‘nearest‘: 最近项插值
‘linear’: 线性插值
‘spline’: 立方样条插值
‘cubic’: 立方插值
 

close all
clear,clc

x=100:100:500;  %已知节点数据
y=100:100:400;
z=[636    697    624    478   450  
   698    712    630    478   420
   680    674    598    412   400
   662    626    552    334   310];

pp=csape({x,y},z') %采用3次样条插值

xi=100:10:500;yi=100:10:400;  %要插值的点
cz=fnval(pp,{xi,yi});          %返回字（xi，yi）处的值

[i,j]=find(cz==max(max(cz)))  %找最高点的地址
x=xi(i),y=yi(j),zmax=cz(i,j)  %求最高点的坐标 

二、插值节点为散乱节点

散乱节点:给出了一些3维空间数据点的x、y、z坐标，但不像网格节点那样整齐。例1和例2一对比就明白了。使用函数griddata()，常见形式和简要说明如下:

(1) vq = griddata( x,y, v ,xq, yq)
使v=fx,y)形式的曲面与向量(xy.v)中的散点数据拟合。gridata函数在(xq,yq)指定的查询点对曲面进行插值并返回插入的值vq。曲面始终穿过×和y定义的数据点。

(2) vq = griddata(x,y,z , v ,xq,yq,zq)拟合v= f(x,y,z)形式的超曲面。

(3)vq = griddata(_,method)
使用上述语法中的任何输入参数指定计算vq所用的插值方法。method可以是’linear’、’nearest 、’natural’、 ‘cubic’或’v4’。默认方法为‘linear’。

(4)[Xq, Yq,vq] = griddata(x,y,v ,xq,yq)或[Xq,Yq, vq] = griddata(x,y ,v , xq, yq,method)
还返回Xq和Yq，其中包含查询点的网格坐标。
更多内容请查阅帮助文档。
 

close all
clc, clear

x=[129,140,103.5,88,185.5,195,105,157.5,107.5,77,81,162,162,117.5];
y=[7.5,141.5,23,147,22.5,137.5,85.5,-6.5,-81,3,56.5,-66.5,84,-33.5];
z=-[4,8,6,8,6,8,8,9,9,8,8,9,4,9];

xmm=minmax(x)  %求x的最小值和最大值
ymm=minmax(y)  %求y的最小值和最大值

xi=xmm(1):xmm(2); %指定查询点（插值点）
yi=ymm(1):ymm(2);

%使 v = f(x,y) 形式的曲面与向量 (x,y,v) 中的散点数据拟合。
% griddata 函数在 (xq,yq) 指定的查询点对曲面进行插值并返回插入的值 vq。
% 曲面始终穿过 x 和 y 定义的数据点。
zi1=griddata(x,y,z,xi,yi','cubic'); %立方插值
zi2=griddata(x,y,z,xi,yi','nearest'); %最近点插值

zi=zi1;  %立方插值和最近点插值的混合插值的初始值
zi(isnan(zi1))=zi2(isnan(zi1))  %把立方插值中的不确定值换成最近点插值的结果

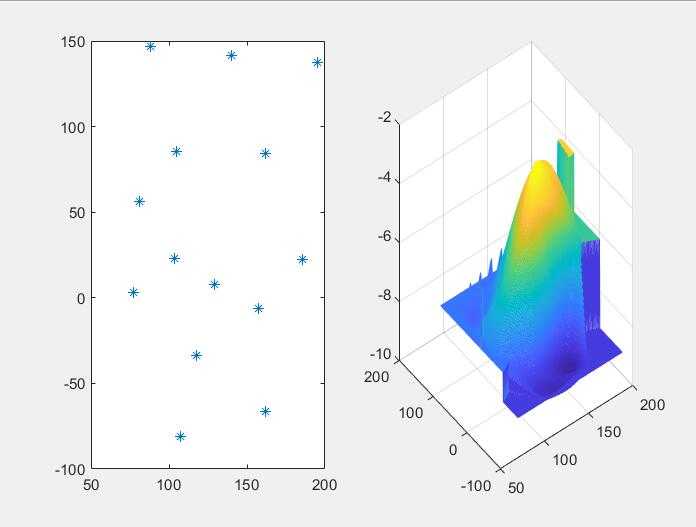
subplot(1,2,1), plot(x,y,'*')
subplot(1,2,2), mesh(xi,yi,zi)