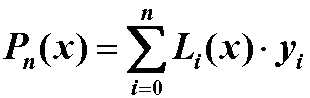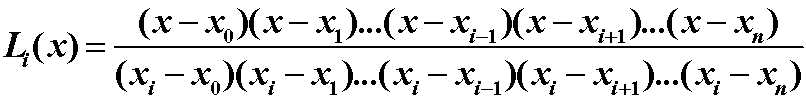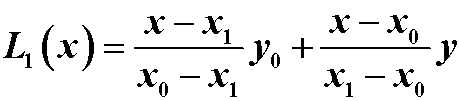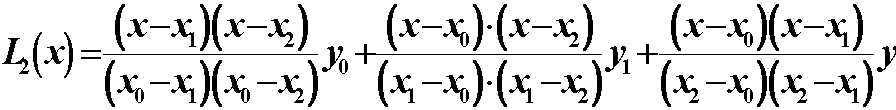一、一元函数插值
已知函数y=f(x)在区间[a,b]上的n+1个不同点
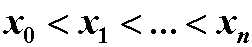
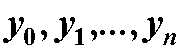
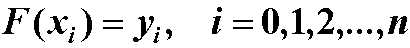
n次代数插值:已知f(x)在n+1个点x0,x1,…,xn处的函数值为 y0,y1,…,yn , 求一个n次多项式函数Pn(x),使其满足: Pn(xi)=yi, (i=0,1,…,n). 若Pn(x)按下述方式构造,称为拉格朗日插值
其中Li(x) 为n次多项式:
称为拉格朗日插值基函数.
特别地:
(1)已知两个节点时,得线性插值多项式:
(2)已知三个节点时,得抛物插值多项式:
(3)已知n+1个节点时,可得n次拉格朗日插值多项式。
关于代数插值:
可以看出,当节点较多时,多项式的次数增高,插值函数出现振荡,精度变低。因此,为了保证精度,在节点较多时,一般采用分段插值,但这样在分段点光滑性较差。Matlab采用的多项式插值都是分段插值法。从图形还可以看出,对解析函数,插值精度高;对有奇点的函数,插值精度低。多项式插值对靠近插值区间中点的部分插值精度高,远离中点部分精度低。
规则网点的插值
y=interp1(x0,y0,x,’method’),y是对应x插值后获得的因变量,x0和y0为初始数据的自变量和因变量
Method 的选项有 ‘nearest’, ‘next’, ‘previous’, ‘linear’,‘spline’,‘pchip’, 和 ‘cubic’. 缺省的机器设置为’linear’.
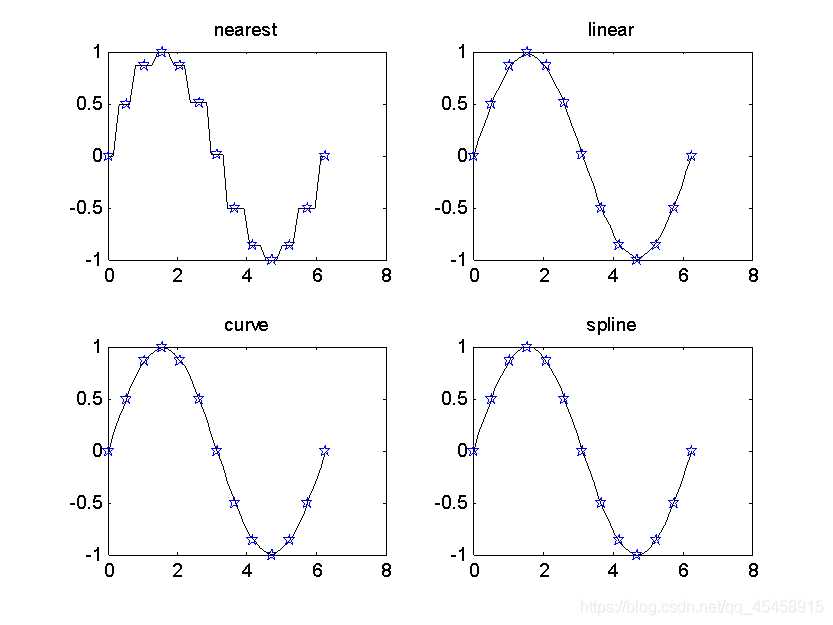
插值效果:
参考程序:
xdata=0:pi/6:2*pi;
ydata=sin(xdata);
x=0:pi/20:2*pi;
subplot(2,2,1)
y=interp1(xdata,ydata,x,’nearest’);
plot(xdata,ydata,’p’,x,y,’k-‘)
title(‘nearest’)
subplot(2,2,2)
y=interp1(xdata,ydata,x,’linear’);
plot(xdata,ydata,’p’,x,y,’k-‘)
title(‘linear’)
subplot(2,2,3)
y=interp1(xdata,ydata,x,’cubic’);
plot(xdata,ydata,’p’,x,y,’k-‘)
title(‘cubic’)
subplot(2,2,4)
y=interp1(xdata,ydata,x,’spline’);
plot(xdata,ydata,’p’,x,y,’k-‘)
title(‘spline’)
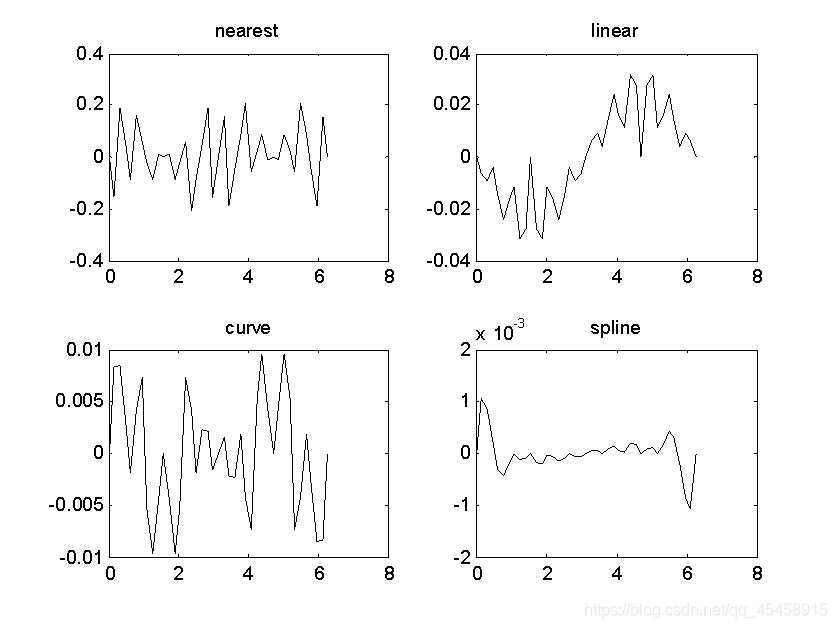
插值误差:
参考程序:
xdata=0:pi/6:2*pi;
ydata=sin(xdata);
x=0:pi/20:2*pi;
yy=sin(x);
subplot(2,2,1)
y=interp1(xdata,ydata,x,’nearest’);
plot(x,y-yy,’k-‘)
title(‘nearest’)
subplot(2,2,2)
y=interp1(xdata,ydata,x,’linear’);
plot(x,y-yy,’k-‘)
title(‘linear’)
subplot(2,2,3)
y=interp1(xdata,ydata,x,’curve’);
plot(x,y-yy,’k-‘)
title(‘curve’)
subplot(2,2,4)
y=interp1(xdata,ydata,x,’spline’);
plot(x,y-yy,’k-‘)
title(‘spline’)
小tips:插值中使用较多的是分段线性插值和三次样条插值。
三次样条插值是解决一维插值问题最常用的方法, Matlab中实现三次样条插值的方法有:
yi=interp1(x,y,xi,’spline’)
使用spline函数:
yi=spline(x, y, xi) ,效果同 1
pp=spline(x, y),获得三次样条插值的分段多项式pp,可使用ppval计算插值
使用csape函数:pp=csape(x, y),可以添加参数选择边界条件
例1:通过实验测得某函数的一组数据如下,试作出其插值函数的图形。
解法一:
x=[0,3,5,7,9,11,12,13,14,15];
y=[0,1.2,1.65,2.1,2.15,2.0,1.85,1.65,1.55,1.25];
xi=0:0.1:15;
yi=interp1(x,y,xi, ‘spline’);
yi1=interp1(x,y,xi, ‘linear’);
yi2=interp1(x,y,xi, ‘cubic’);
plot(x,y,’*’,xi,yi,’r-‘,xi,yi1,’b-‘,xi,yi2,’g-‘)
legend(‘节点’,’三次样条插值’,’线性插值’,’立方插值’)
解法二:
x=[0,3,5,7,9,11,12,13,14,15];
y=[0,1.2,1.65,2.1,2.15,2.0,1.85,1.65,1.55,1.25];
xx=0: 0.1: 15;
S=csape(x, y);
%Sa=spline(x, y) ;
P=S.coefs;
%Pa=Sa.coefs;
yy=ppval(S,xx);
plot(x,y,’o’,xx,yy,’r’);
关于pp形式:
pp就是分段多项式,百语句形如:
breaks = -5:-1;
coefs = -22:-11;
pp = ppmak(breaks,coefs)
其中:breaks就是各度段的端点值,-5,-4,-3,-2,-1,有问4个区间
coefs就是每段多项式的系数,答共有12个值,12/4=3,则有回4个多项式,每个多项式的最高次答数是3
二、 二元函数插值
网格节点数据插值
函数:interp2
格式:z=interp2(x0, y0, z0, x, y, ’method’)
x0,y0,z0:插值节点坐标,要求x0, y0单调;
x, y是被插值点的横坐标与纵坐标( x, y不能超过x0,y0的范围),z是被插值点的函数值。
Method:(1)nearest 最邻近插值,(2)linear 双线性插值,(3)cubic双三次插值,默认为双线性插值。
例2:要在一山区修建公路,首先测得一些点的高程(见附件,表中数据为坐标点的高程,单位:米,y轴正向为北)绘制该地地貌图。
4800
1350
1370
1390
1400
1410
960
940
880
800
690
570
430
290
210
150
4400
1370
1390
1410
1430
1440
1140
1110
1050
950
820
690
540
380
300
210
4000
1380
1410
1430
1450
1470
1320
1280
1200
1080
940
780
620
450
370
350
3600
1420
1430
1450
1480
1500
1550
1510
1430
1300
1200
980
850
750
550
500
3200
1430
1450
1460
1500
1550
1600
1550
1600
1600
1600
1550
1500
1500
1550
1500
2800
950
1190
1370
1500
1200
1100
1550
1600
1550
1380
1070
900
1050
1150
1200
2400
910
1090
1270
1500
1200
1100
1350
1450
1200
1150
1010
880
1000
1050
1100
2000
880
1060
1230
1390
1500
1500
1400
900
1100
1060
950
870
900
930
950
1600
830
980
1180
1320
1450
1420
1400
1300
700
900
850
840
380
780
750
1200
740
880
1080
1130
1250
1280
1230
1040
900
500
700
780
750
650
550
800
650
760
880
970
1020
1050
1200
830
800
700
300
500
550
480
350
400
510
620
730
800
850
870
850
780
720
650
500
200
300
350
320
0
370
470
550
600
670
690
670
620
580
450
400
300
100
150
250
y/x
0
400
800
1200
1600
2000
2400
2800
3200
3600
4000
4400
4800
5200
5600
解:
A = xlsread(‘新建 XLSX 工作表.xlsx’);
[xx,yy]=size(A);
Z=A([1:xx-1],[2:yy]);
x=0:400:5600;
y=4800:-400:0;
[X,Y]=meshgrid(x,y);
surf(X,Y,Z); %离散图
figure(2);
xi=linspace(0, 5600, 80);
yi=linspace(0, 4800, 80);
[Xi,Yi]=meshgrid(xi, yi);
%%——————————-
Zi=interp2(X,Y,Z,Xi,Yi,’linear’); %二元插值 linear
surf(Xi,Yi,Zi);
%%——————————-
figure(3)
Zi=interp2(X,Y,Z,Xi,Yi,’spline’); %二元插值 spline
surf(Xi,Yi,Zi);
%%——————————-
figure(4)
t=0:100:1600;
[c,h]= contourf(Xi,Yi,Zi,t); %等高线
clabel(c, h)
colormap cool
colorbar
散点数据插值函数
已知n个插值节点(xi, yi, zi), (i=1,2,…,n), 求在点(x,y)处的插值z, matlab提供函数griddata。
格式:cz=griddata(x,y,z,cx,cy,’method’)
其中x,y,z 均为n 维向量,指明所给数据点(插值节点)的横坐标、纵坐标和竖坐标。cx, cy是给定被插值点的横坐标和纵坐标,cz为相应点的竖坐标。
若cx,cy是向量,则给定以它们所确定网格点的横坐标和纵坐标,这时要求cx,cy一个为行向量一个为列向量。 编程时也可先用meshgrid将cx,cy定义成网格矩阵。
例3:在某海域测得一些点(x,y)处的水深z(英尺)如下表,船的吃水深度为5英尺,在矩形区域(75,200)×(-50,150)里那些地方船要避免进入。
x
129
140
103.5
88
185.5
195
105
157.5
107.5
77
81
162
162
117.5
y
7.5
141.5
23
147
22.5
137.5
85.5
-6.5
-81
3
56.5
-66.5
84
-33.5
z
4
8
6
8
6
8
8
9
9
8
8
9
4
9
解:
x=[129,140,103.5,88,185.5,195,105,157.5,107.5,77,81,162,162,117.5];
y=[7.5,141.5,23,147,22.5,137.5,85.5,-6.5,-81,3,56.5,-66.5,84,-33.5];
z=-[4,8,6,8,6,8,8,9,9,8,8,9,4,9];
[x1,y1]=meshgrid(75:5:200,150:-5:-50);
z1=griddata(x,y,z,x1,y1,’v4′);
surf(x1,y1,z1)
figure(2)
[c,h]=contourf(x1,y1,z1);
clabel(c,h)
三、 三元函数插值
函数:interp3
格式:v = interp3(x0, y0, z0, v0 , x, y, z ,’method’)
x0,y0,z0,v0为插值数据,x,y,z为被插值的范围,v代表val
虽然三元图像不能直观的画图观察,但是可以通过切割观察剖面,配合slice函数观察切片情况
格式:slice(X,Y,Z,V,sx,sy,sz)
X,Y,Z,V为数据,sx,sy,sz可决定切片形式和位置
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/36007.html