前言
提示:本文主要讲述行列式的求解方法,所以本文侧重于方法的讲解,而并非推导。主要思路为从三阶行列式举例,再过渡到高阶行列式的通用方法 。
以下是本篇文章正文内容:
一、对角线法
▍以三阶行列式为例:
D 3 = ∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ D_3= \left| \begin{matrix} a_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\\ \end{matrix} \right| D3=∣∣∣∣∣∣a11a21a31a12a22a32a13a23a33∣∣∣∣∣∣
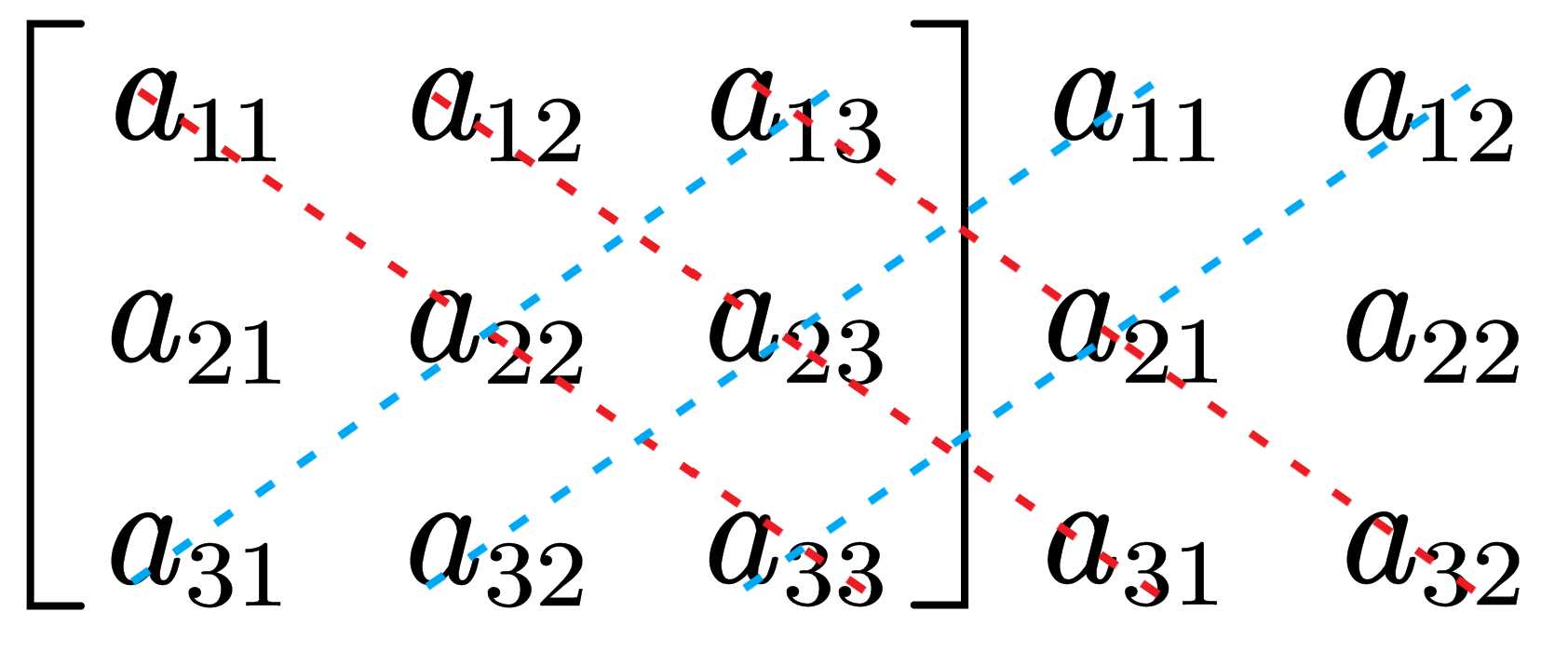
①将第一、二列平移到行列式右侧
②如图做出六条斜对角线
③对角线上的元素相乘,红色相加的和 减去 蓝色相加的和
D 3 = D_3= D3=
a 11 a 22 a 33 + a 12 a 23 a 31 + a 13 a 21 a 32 a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32} a11a22a33+a12a23a31+a13a21a32
− a 13 a 22 a 31 − a 11 a 23 a 32 − a 12 a 21 a 33 -a_{13}a_{22}a_{31}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33} −a13a22a31−a11a23a32−a12a21a33
对角线法也是三阶行列式计算使用最广泛的方法
▍ 对角线法适用于二、三阶行列式,对于更高阶的行列式暂时未找到规律
二、代数余子式法
▍以三阶行列式为例:
例 : D 3 = ∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ 例:D_3= \left| \begin{matrix} a_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\\ \end{matrix} \right| 例:D3=∣∣∣∣∣∣a11a21a31a12a22a32a13a23a33∣∣∣∣∣∣
以 第 一 行 展 开 , 得 D 3 = 以第一行展开,得D_3= 以第一行展开,得D3=
= ( − 1 ) 1 + 1 a 11 M 11 + ( − 1 ) 1 + 2 a 12 M 12 + ( − 1 ) 1 + 3 a 13 M 13 =\left( -1 \right) ^{1+1}a_{11}M_{11}+\left( -1 \right) ^{1+2}a_{12}M_{12}+\left( -1 \right) ^{1+3}a_{13}M_{13} =(−1)1+1a11M11+(−1)1+2a12M12+(−1)1+3a13M13
= a 11 ∣ a 22 a 23 a 32 a 33 ∣ − a 12 ∣ a 21 a 23 a 31 a 33 ∣ + a 13 ∣ a 21 a 22 a 31 a 32 ∣ =a_{11}\left| \begin{matrix} a_{22}& a_{23}\\ a_{32}& a_{33}\\ \end{matrix} \right|-a_{12}\left| \begin{matrix} a_{21}& a_{23}\\ a_{31}& a_{33}\\ \end{matrix} \right|+a_{13}\left| \begin{matrix} a_{21}& a_{22}\\ a_{31}& a_{32}\\ \end{matrix} \right| =a11∣∣∣∣a22a32a23a33∣∣∣∣−a12∣∣∣∣a21a31a23a33∣∣∣∣+a13∣∣∣∣a21a31a22a32∣∣∣∣
对于任一行(列)都可进行展开
▍例n阶行列式:
D n = ∣ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋮ a n 1 a n 2 ⋯ a n n ∣ D_n=\left| \begin{matrix} a_{11}& a_{12}& \cdots& a_{1n}\\ a_{21}& a_{22}& \cdots& a_{2n}\\ \vdots& \vdots& & \vdots\\ a_{n1}& a_{n2}& \cdots& a_{nn}\\ \end{matrix} \right| Dn=∣∣∣∣∣∣∣∣∣a11a21⋮an1a12a22⋮an2⋯⋯⋯a1na2n⋮ann∣∣∣∣∣∣∣∣∣
以第 i 行展开:
= ( − 1 ) i + 1 a i 1 M i 1 + ( − 1 ) i + 2 a i 2 M i 2 + ⋯ + ( − 1 ) i + n a i n M i n =\left( -1 \right) ^{i+1}a_{i1}M_{i1}+\left( -1 \right) ^{i+2}a_{i2}M_{i2}+\cdots +\left( -1 \right) ^{i+n}a_{in}M_{in} =(−1)i+1ai1Mi1+(−1)i+2ai2Mi2+⋯+(−1)i+nainMin
以第 j 列展开:
= ( − 1 ) 1 + j a 1 j M 1 j + ( − 1 ) 2 + j a 2 j M 2 j + ⋯ + ( − 1 ) n + j a n j M n j =\left( -1 \right) ^{1+j}a_{1j}M_{1j}+\left( -1 \right) ^{2+j}a_{2j}M_{2j}+\cdots +\left( -1 \right) ^{n+j}a_{nj}M_{nj} =(−1)1+ja1jM1j+(−1)2+ja2jM2j+⋯+(−1)n+janjMnj
例 : ∣ 0 1 0 2 15 3 1 41 2 ∣ = ( − 1 ) 1 + 2 ∣ 3 2 2 1 ∣ = 1 例: \left| \begin{matrix} 0& 1& 0\\ 2& 15& 3\\ 1& 41& 2\\ \end{matrix} \right|=\left( -1 \right) ^{1+2}\left| \begin{matrix} 3& 2\\ 2& 1\\ \end{matrix} \right|=1 例:∣∣∣∣∣∣02111541032∣∣∣∣∣∣=(−1)1+2∣∣∣∣3221∣∣∣∣=1
本例中,利用代数余子式法能够简便运算
三、等价转化法
①行列式的某一行(列)的各元素乘同一数然后加到另一行(列)对应的元素上去,行列式不变
②行列式中某一行(列)的所有元素的公因子可以提到行列式记号的外面
转化法的核心思想是将行列式转化成上三角行列式
直接举例:
D 4 = ∣ 3 1 1 1 1 3 1 1 1 1 3 1 1 1 1 3 ∣ D_4=\left| \begin{matrix} 3& 1& 1& 1\\ 1& 3& 1& 1\\ 1& 1& 3& 1\\ 1& 1& 1& 3\\ \end{matrix} \right| D4=∣∣∣∣∣∣∣∣3111131111311113∣∣∣∣∣∣∣∣
∣ 3 1 1 1 1 3 1 1 1 1 3 1 1 1 1 3 ∣ = r 1 + r 2 + r 3 + r 4 ∣ 6 6 6 6 1 3 1 1 1 1 3 1 1 1 1 3 ∣ = r 1 ÷ 6 6 ∣ 1 1 1 1 1 3 1 1 1 1 3 1 1 1 1 3 ∣ \left| \begin{matrix} 3& 1& 1& 1\\ 1& 3& 1& 1\\ 1& 1& 3& 1\\ 1& 1& 1& 3\\ \end{matrix} \right|\xlongequal{r_1+r_2+r_3+r_4}\left| \begin{matrix} 6& 6& 6& 6\\ 1& 3& 1& 1\\ 1& 1& 3& 1\\ 1& 1& 1& 3\\ \end{matrix} \right|\xlongequal{r_1\div 6}6\left| \begin{matrix} 1& 1& 1& 1\\ 1& 3& 1& 1\\ 1& 1& 3& 1\\ 1& 1& 1& 3\\ \end{matrix} \right| ∣∣∣∣∣∣∣∣3111131111311113∣∣∣∣∣∣∣∣r1+r2+r3+r4∣∣∣∣∣∣∣∣6111631161316113∣∣∣∣∣∣∣∣r1÷66∣∣∣∣∣∣∣∣1111131111311113∣∣∣∣∣∣∣∣
= r 2 − r 1 , r 3 − r 1 , r 4 − r 1 6 ∣ 1 1 1 1 0 2 0 0 0 0 2 0 0 0 0 2 ∣ = 6 × 1 × 2 × 2 × 2 = 48 \xlongequal{r_2-r_1,r_3-r_1,r_4-r_1}6\left| \begin{matrix} 1& 1& 1& 1\\ 0& 2& 0& 0\\ 0& 0& 2& 0\\ 0& 0& 0& 2\\ \end{matrix} \right|=6\times1\times 2\times 2\times 2=48 r2−r1,r3−r1,r4−r16∣∣∣∣∣∣∣∣1000120010201002∣∣∣∣∣∣∣∣=6×1×2×2×2=48
四、逆序数法
▍以三阶行列式为例
D 3 = ∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ = ∑ ( − 1 ) t a 1 p 1 a 2 p 2 a 3 p 3 D_3=\left| \begin{matrix} a_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\\ \end{matrix} \right| =\sum{\left( -1 \right) ^ta_{1p_1}a_{2p_2}a_{3p_3}} D3=∣∣∣∣∣∣a11a21a31a12a22a32a13a23a33∣∣∣∣∣∣=∑(−1)ta1p1a2p2a3p3
t 为排列 p 1 p 2 p 3 的逆序数 t\text{为排列 }p_1p_2p_3\ \text{的逆序数} t为排列 p1p2p3 的逆序数
其 中 p 1 、 p 2 、 p 3 ≤3,且各不相同 其中p_1\text{、}p_2\text{、}p_3\text{≤3,且各不相同} 其中p1、p2、p3≤3,且各不相同
▍对于n阶行列式:
D n = ∣ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋮ a n 1 a n 2 ⋯ a n n ∣ D_n=\left| \begin{matrix} a_{11}& a_{12}& \cdots& a_{1n}\\ a_{21}& a_{22}& \cdots& a_{2n}\\ \vdots& \vdots& & \vdots\\ a_{n1}& a_{n2}& \cdots& a_{nn}\\ \end{matrix} \right| Dn=∣∣∣∣∣∣∣∣∣a11a21⋮an1a12a22⋮an2⋯⋯⋯a1na2n⋮ann∣∣∣∣∣∣∣∣∣
= ∑ ( − 1 ) t a 1 p 1 a 2 p 2 ⋯ a n p n =\sum{\left( -1 \right) ^ta_{1p_1}a_{2p_2}\cdots a_{np_n}} =∑(−1)ta1p1a2p2⋯anpn
t 为排列 p 1 p 2 ⋯ p n 的逆序数 t\text{为排列 }p_1p_2\cdots p_n\ \text{的逆序数} t为排列 p1p2⋯pn 的逆序数
其 中 p 1 、 p 2 ⋯ p n ≤n,且各不相同 其中p_1\text{、}p_2\cdots p_n\text{≤n,且各不相同} 其中p1、p2⋯pn≤n,且各不相同
前三种方法的本质其实都是逆序数法,逆序数法也是行列式求解最基础的方法,但使用起来更加复杂
总结
本文讲述了四种行列式的计算方法:
▍其中对角线法,是使用最简单、最广泛的方法
▍代数余子式法和等价转化法,在特定情况下能极大程度上简便运算,但需要读者对行列式进行灵活地观察
▍逆序数法,是一种更加基础的方法,使用起来比较复杂
提示:以上是本人关于行列式学习的体会,若有错误,欢迎大家批评和交流(*^▽ ^*)/
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/37503.html