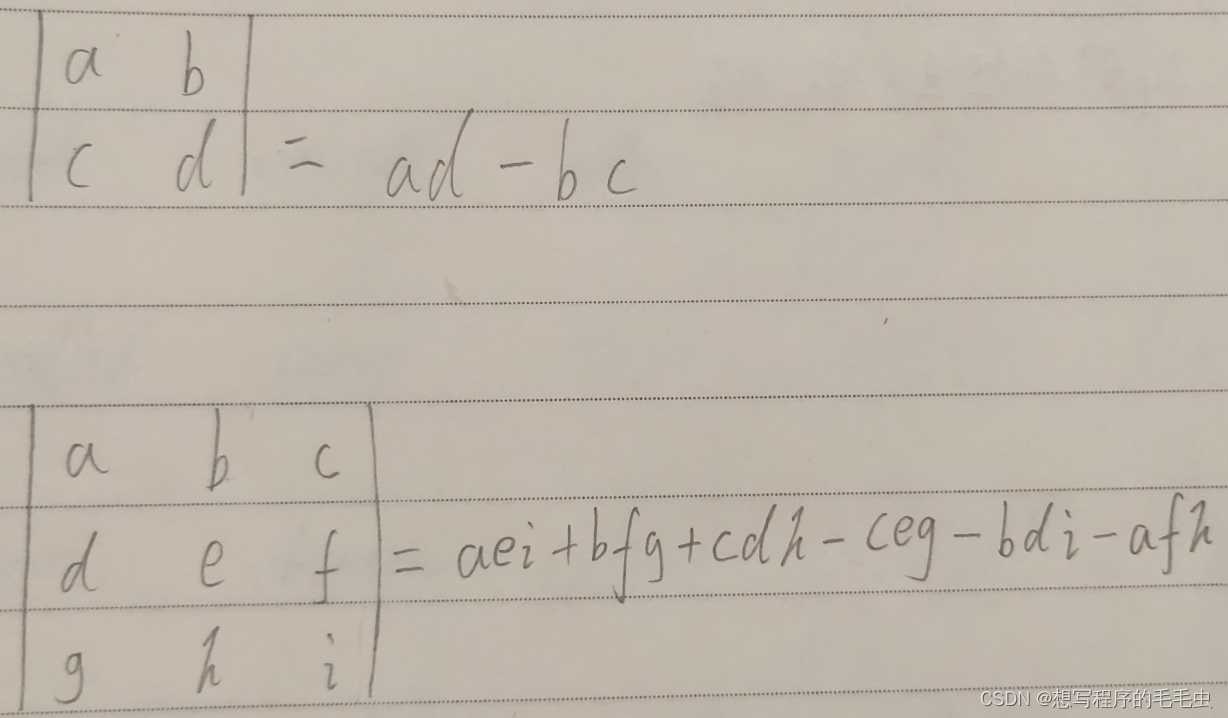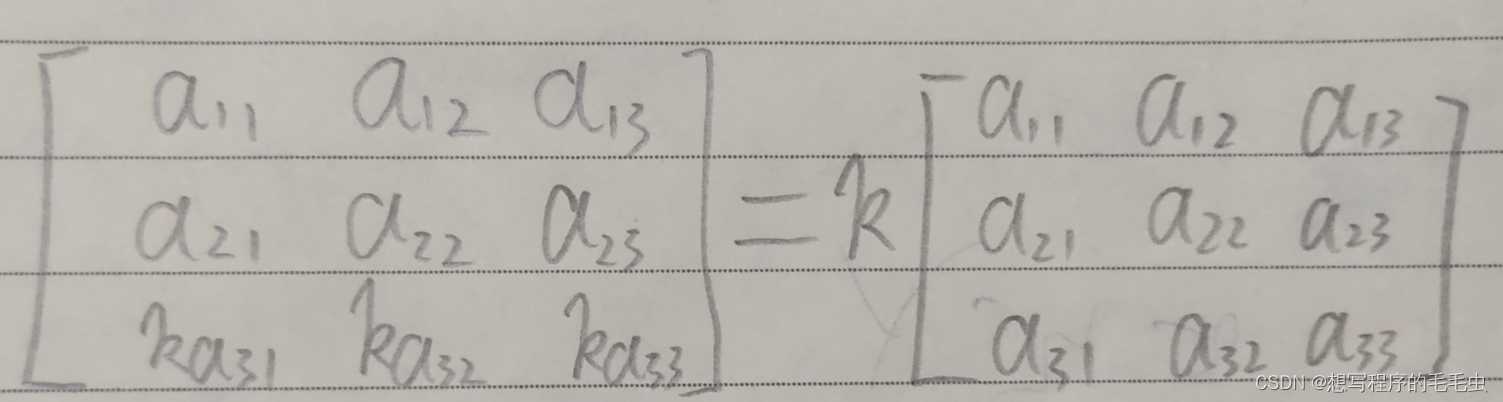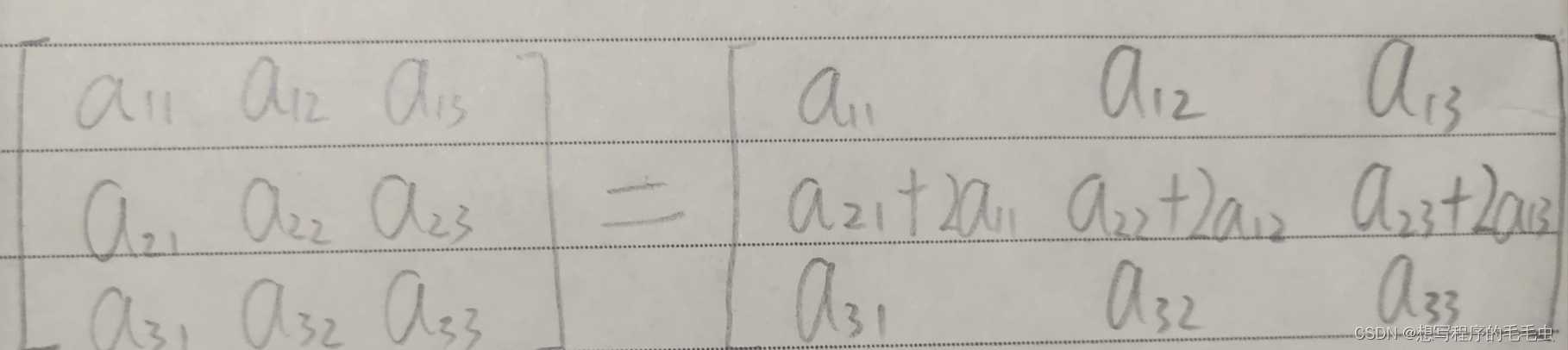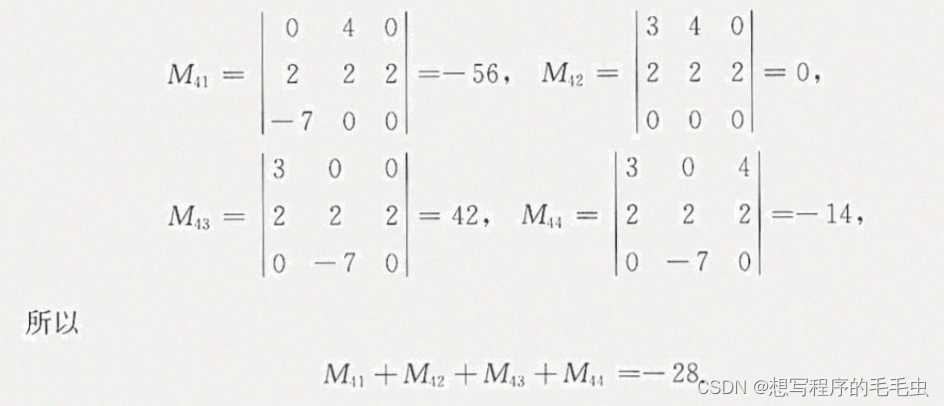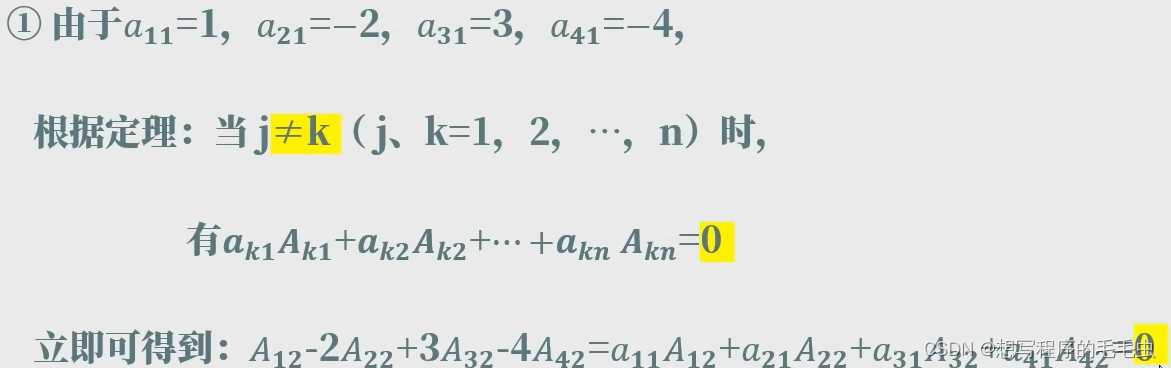线性代数（1）：行列式和展开式

一、行列式

（1）定义

        矩阵的行列式是线性代数的一个重要组成部分，是基于矩阵所包含的行列数据计算得到的一个标量。

        矩阵的行列式是通过正对角线数值乘积减去反对角线的数值乘积得出的；

         例：

        而在上（下）三角矩阵和只有对角线元素的矩阵中，因为存在零值所以可以通过对角线相乘计算出该行列式的的结果，由于 3 阶以上矩阵的行列式结果值计算量会比较大，所以我们通常将 3 阶以上的行列式转换成上（下）三角矩阵进行计算；

        例：

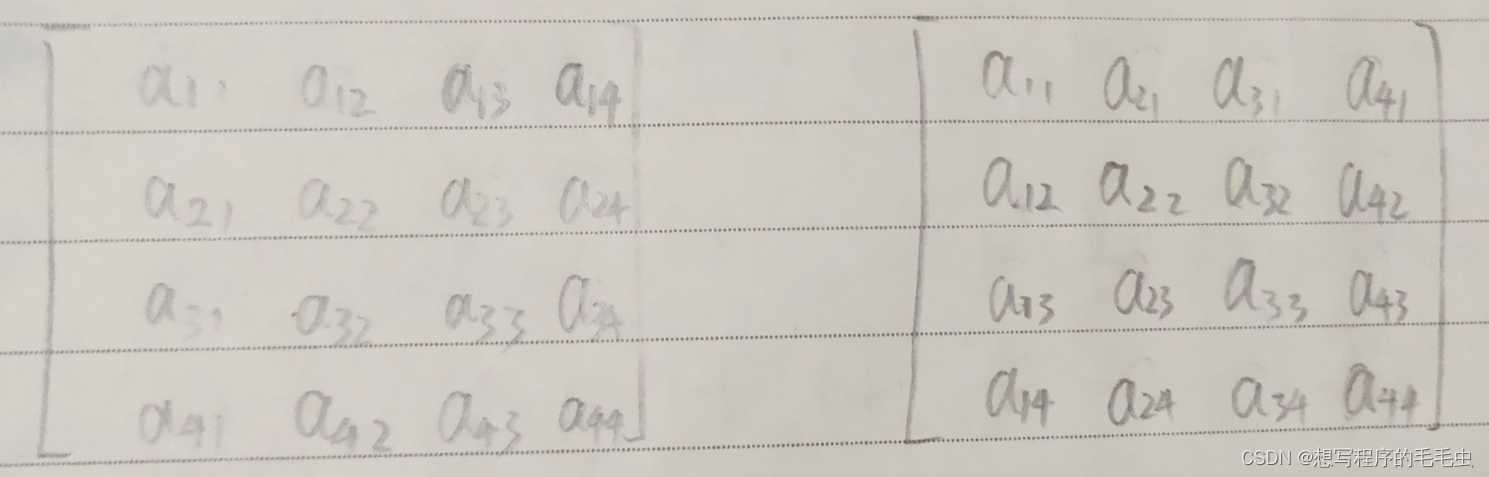
这两个矩阵的结果数值皆为( a11 * a22 * a33 * a44 )

a11代表的为第一行第一列的元素，a12代表的为第一行第二列的元素。

a21代表的为第二行第一列的元素，a22代表的为第二行第二列的元素。

……   ……

（2）性质

        a. 一个行列式的转置行列式与它本身相等；

        b. 行列式的某一行（列）同时乘以 k ，相当于使用 k 乘以整个行列式；

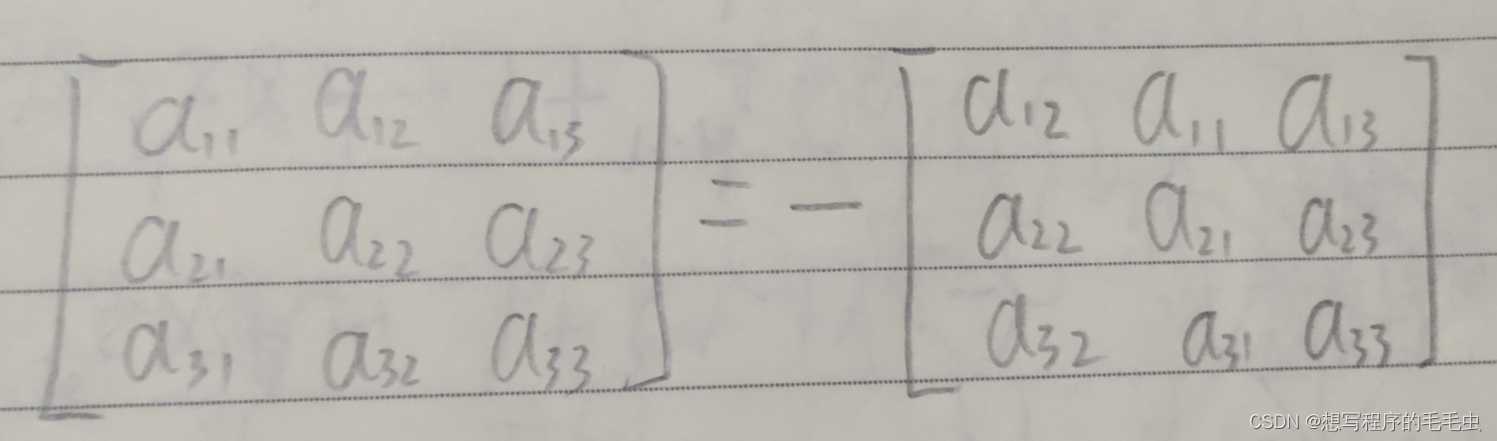
        c. 行列式的两行（列）交换位置，整个行列式的符号发生改变；

        d. 行列式的某一行（列）的所有元素同时加（减）到另一 k 倍行（列）上，整个行列式不会发生改变；

        e. 若行列式的某一行（列）的所有元素都是两个数相加（减） ，可以将此行列式拆分为两个行列式相加（减）；

二、逆序数

（1）定义

        有n个元素排列，从第1个元素开始直至最后一个元素依次对排列在前的元素进行比较，如果有比当前元素更大的值排列于该元素之前，那么这个元素数列就是一个逆序排列。

        逆序数的计算规则为所有元素的逆序个数之和，即第1个元素前的逆序元素个数记录为X1,第2个元素前的逆序元素个数记录为X2， ……   …… 第n个元素前的逆序元素个数记录为Xn。最终该序列的逆序数的大小为 (X1 + X2 + ……   …… + Xn )

（2）

        例：求排列 648157 的逆序数

        解： 6排在首位，X1为0；                          4前面有1个更大的元素，X2为1；

                8前面没有更大的元素，X3为0；        1前面有3个更大的元素，X4为3；

                5前面有2个更大的元素，X5为2；      7前面有1个更大的元素，X6为1；

        于是这个排列的逆序数为:

                                ( X1 + X2 + X3 + X4 + X5 + X6 ) = 0 + 1 + 0 + 3 + 2 + 1 = 7 ;

三、展开式

（1）余子式和代数余子式

        余子式：顾名思义余子式就是余下的子式，一般余子式用符号M来表示，M ij 表示将行列式中i行与j列全部删除后所余下的数据组成的行列式；

        代数余子式：一般用符号A表示，A ij 表示 在M ij 的基础上乘以pow( -1 , i+j )，即A ij = pow( -1 ，i+j ) * M ij ；

（2）展开式定义

        a. 展开定理：展开式等于它的任意一行的所有元素与他们各自代数余子式的乘积之和；（ k = j 时）

                        a k1 * A k1 + a k2 * A k2 + ……   …… + a kn * A kn ( k 为行数)

        b. 零值定理：展开式等于0； （ k ≠ j 时）

                        a k1 * A k1 + a k2 * A k2 + ……   …… + a kn * A kn = 0 ( k 为行数)

        例1：

        解：

            例2：

解：