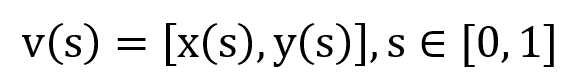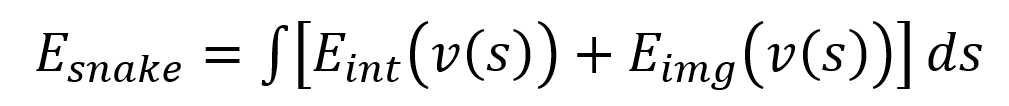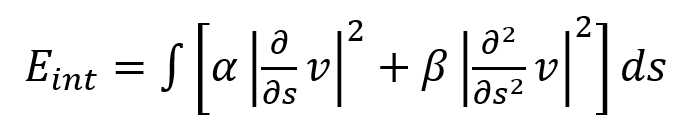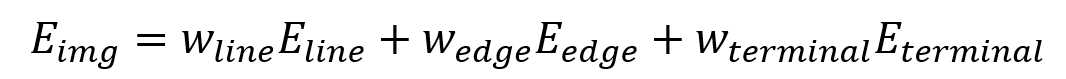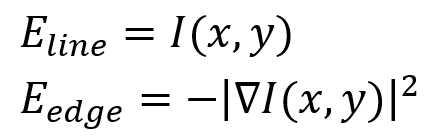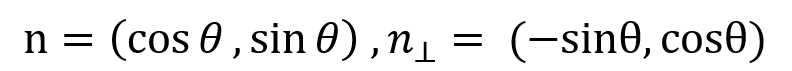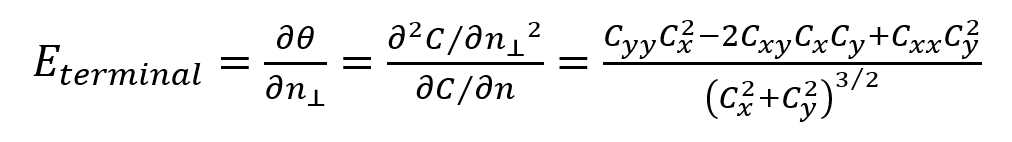Snake算法与遥感影像应用，python matlab对比

最近，在做一个关于遥感信息提取的工作，发现一个Snake模型可以应用于图像分割，初学Python和Matlab，因此使用这两门语言进行了一定的了解和深入学习，这也是我的第一篇博客，欢迎一起讨论。

Snake算法原理

这个模型是基于“分割线是有能量的”这一基础进行的研究，当轮廓线稳定到能量最小处时，就是分割的终点，因此需要输入一个初始轮廓线用以计算能量，在运算过程中，能量是朝着减小的方向进行的。

相关公式如下：

Snake的边界由一组控制点表示，s是以傅立叶变换形式描述边界的自变量

Snake能量函数是有内部能量函数和外部能量函数组成。

• 内部能量控制轮廓的平滑性和连续性，由弹性势能和弯曲势能组成，其中弹性势能为v一阶导数的模，弯曲势能为v二阶导数的模。

• 外部能量（又称图像力）由线性能量Eline、边缘能量Eedge和终端能量Eterminal三者加权相加而成。

• 设定Eline为图像强度，Eedge为亮度的梯度变化

• 定义C(x,y)为高斯滤波（可否不进行滤波操作？）后的图像，θ是(x,y)处的梯度角度

可以得到Eterminal

关于优化：作者用数值方法进行推导，得到了一个迭代的方程式（这个我不太清楚），主要来源于以下文章

老笨妞 snake算法总结

田问渠Carlnait 主动轮廓模型——Snake分割算法 matlab源码

在此也借鉴了许多的博客内容，在这一部分不过多赘述。

由于轮廓点信息都是投影坐标，因此需要将投影坐标先转换为行列式坐标。在转换时，matlab数组序号起始是1，而python数组起始是0，因此在计算x，y的行列式坐标时，应相应加减0.5

Matlab 进行计算（代码主要来源于以上所列博客及matlab官网，并根据实际情况进行修改）

1.打开影像与分割线

Former=shaperead("修改前线/6_former.shp");
[Igs,R]=geotiffread("校正背景/6.tif");
Igs=double(Igs);
x=(Former.X-R.XWorldLimits(1))/R.CellExtentInWorldX + 0.5;
y=(Former.Y-R.YWorldLimits(2))/-R.CellExtentInWorldY + 0.5;%第y行 第x列
if(length(x)==length(y))
    c=length(x);
    for i=1:c-1
        x_temporary(i)=x(i);
        y_temporary(i)=y(i);
    end
    x=x_temporary;
    y=y_temporary;
%     x(:,c)=x(:,1);% shp文件中已经是环状点集合，因此不需要把第一个点添加到最后
%     y(:,c)=y(:,1);%
    xy = [x;y];
end

2.样条曲线差值（不过我没有进行插值）

% 样条曲线差值
t=1:c;
ts = 1:0.1:c;
xys = spline(t,xy,ts);
xs = xys(1,:);
ys = xys(2,:);
% 样条差值效果
hold on
temp=plot(x,y,'ro',xs,ys,'b.');
legend(temp,'原点','插值点');

 3.Snake主体部分（这一部分除参数外基本一样）

******需要改动的一个地方是：栅格图像的行列号坐标与实际坐标是有差异的，差异在0.5个空间分辨率上，例如：行列坐标计算为2的坐标点事实上在栅格中是位于第二个像元和第三个像元之间的共享边界上，因此不能直接使用计算得到的距离坐标来代入到矩阵坐标中进行计算。

% =========================================================================
%                     Snakes算法实现部分
% =========================================================================
NIter =200; % 迭代次数
alpha=0.2; beta=0.2; gamma = 1; kappa = 0.1;
wl = 0.06; we=0.16; wt=0.78;
[row,col] = size(Igs);

% 图像力-线函数
Eline = Igs;
% 图像力-边函数
[gx,gy]=gradient(Igs);
Eedge = -1*sqrt((gx.*gx+gy.*gy));
% 图像力-终点函数
% 卷积是为了求解偏导数，而离散点的偏导即差分求解
m1 = [-1 1]; 
m2 = [-1;1];
m3 = [1 -2 1]; 
m4 = [1;-2;1];
m5 = [1 -1;-1 1];
cx = conv2(Igs,m1,'same');
cy = conv2(Igs,m2,'same');
cxx = conv2(Igs,m3,'same');
cyy = conv2(Igs,m4,'same');
cxy = conv2(Igs,m5,'same');

for i = 1:row
    for j= 1:col
        Eterm(i,j) = (cyy(i,j)*cx(i,j)*cx(i,j) -2 *cxy(i,j)*cx(i,j)*cy(i,j) + cxx(i,j)*cy(i,j)*cy(i,j))/((1+cx(i,j)*cx(i,j) + cy(i,j)*cy(i,j))^1.5);
    end
end

% 外部力 Eext = Eimage + Econ
Eext = wl*Eline + we*Eedge + wt*Eterm;
% 计算梯度
[fx,fy]=gradient(Eext);

xs=x';%数组序列与坐标之间的差异
ys=y';
[m,n] = size(xs);
[mm,nn] = size(fx);
% 计算五对角状矩阵
% 附录: 公式（14） b(i)表示vi系数(i=i-2 到 i+2)
b(1)=beta;
b(2)=-(alpha + 4*beta);
b(3)=(2*alpha + 6 *beta);
b(4)=b(2);
b(5)=b(1);

A=b(1)*circshift(eye(m),2);
A=A+b(2)*circshift(eye(m),1);
A=A+b(3)*circshift(eye(m),0);
A=A+b(4)*circshift(eye(m),-1);
A=A+b(5)*circshift(eye(m),-2);

% 计算矩阵的逆
[L,U] = lu(A + gamma * eye(m));
Ainv = inv(U) * inv(L); 

figure(1)
for i=1:NIter
    %限制轮廓点在图像内
    for p=1:m
        if(xs(p)<1)
            xs(p)=1;
        end
        if(ys(p)<1)
            ys(p)=1;
        end
        if(xs(p)>col)
            xs(p)=col;
        end
        if(ys(p)>row)
            ys(p)=row;
        end
    end
    ssx = gamma*xs - kappa*interp2(fx,xs,ys);
    ssy = gamma*ys - kappa*interp2(fy,xs,ys);
 
    % 计算snake的新位置
    xs = Ainv * ssx;
    ys = Ainv * ssy;
end

4.显示图像

imshow(Igs,[],'InitialMagnification','fit'); %'[]'是灰度显示，"'InitialMagnification','fit'"是把图像放大显示以匹配对话框大小
hold on;
plot(x',y','b-');
plot([xs;xs(1)], [ys; ys(1)], 'r-');
hold off;

imshow中的参数是为了放大图像可移至matlab小技巧：imshow放大图像显示位置(以合适大小显示)

Python

1.导入相关的包

import gdal
import numpy as np
import osr
import ogr
import os
import csv
from scipy import signal,ndimage,linalg
import matplotlib.pyplot as plt

2.定义附属函数 

cirshift（）  #用于做矩阵的上下循环移位操作，我没有找见python中这个函数，但我认为一定有，有知道的朋友麻烦告知一声哦，谢谢

def circshift(A,K,m=1):
    B=np.array(A)
    x,y=A.shape
    for i in range(0,x):
        for j in range(0,y):
            B[(i+K)%x,j]=A[i,j]
    return B

3.调用部分

Imagefilename="D:\\6.tif"
Linefilename="D:\\6_former.shp"
Igs,xy,xys=Snake_Python(Imagefilename,Linefilename,wl=0.06,we=0.14,wt=0.8)

plt.imshow(Igs,cmap='gray')
plt.plot(xy[0],xy[1])
plt.plot(xys[0],xys[1])#按列叠加在一起
plt.show()

4.Snake函数（主体）

使用python编写的Snake算法基本上是参照Matlab那个算法的流程写下来的，只在部分区域有差异。

def Snake_Python(Imagefilename,Linefilename,alpha=0.2,beta=0.2,gamma = 1,kappa = 0.1,wl = 0.06,we=0.16,wt=0.78,NIter =200):
    #打开遥感影像
    dataset=gdal.Open(Imagefilename)
    im_width=dataset.RasterXSize     #列数
    im_height=dataset.RasterYSize    #行数
    im_bands=dataset.RasterCount     #波段数
    im_geotrans=dataset.GetGeoTransform()   #仿射矩阵
    im_proj=dataset.GetProjection()      #地图投影信息
    im_band=dataset.GetRasterBand(1)
    Igs=im_band.ReadAsArray(0,0,im_width,im_height)
    del dataset
    #关闭图像进程
    Igs=np.double(Igs)
    ######################### 读点数据(存在excel里处理过)
    #with open("D:\\Point_6.csv") as pointprefile:
    #    pointdata=csv.reader(pointprefile)
    #    for pointrow in pointdata:
    #        point.append([pointrow[3],pointrow[4]])
    ##########################        

    #打开shapefile文件得到坐标
    ds=ogr.Open(Linefilename,False) #打开Shape文件（False - read only, True - read/write）
    layer=ds.GetLayer(0)#获取图层
    geomlist=[]#SF数据记录– 几何对象
    feature = layer.GetNextFeature() #获得第一个SF
    while feature is not None:
        geom = feature.GetGeometryRef()#创建Geometry引用geom
        geomlist += [geom.ExportToWkt()]
        feature = layer.GetNextFeature()
    ds.Destroy() 
    #关闭shapefile进程
    
    point=ogr.CreateGeometryFromWkt(geomlist[0]).GetPoints()#导出为string再生成Geometry，其实相当于geom，可以使用geom在循环中使用GetPoints
    point_change=np.array(point)
    x=point_change[:,0]
    y=point_change[:,1]
    x=(x-im_geotrans[0])/im_geotrans[1] -0.5 #投影坐标转换为行列号
    y=(y-im_geotrans[3])/im_geotrans[5] -0.5
    
    # =========================================================================
    #                      Snakes算法实现部分
    # =========================================================================
    #NIter =200; # 迭代次数
    #alpha=0.2; beta=0.2; gamma = 1; kappa = 0.1;
    #wl = 0.06; we=0.16; wt=0.78;
    row,col = Igs.shape

    #数组与矩阵关于方向的说法正好相反，矩阵的x向是同行运算，二维数组的x向是同列运算（第一维度，axis=0）
    #图像力 线函数
    Eline=Igs
    #图像力 边函数
    gy,gx=np.gradient(Igs)
    ############################################################################
    #The gradient is computed using second order accurate central differences  #
    #in the interior points and either first or second order accurate one-sides#
    #(forward or backwards) differences at the boundaries.                     #
    ############################################################################
    Eedge=-1*np.sqrt(gx*gx+gy*gy) #python中 *，dot是点乘；@，multiply是叉乘

    #图像力-终点函数
    #卷积是为了求解偏导数，而离散点的偏导即差分求解
    m1 = [-1,1]
    m2 = [1,-2,1]
    m3 = [[1,-1],[-1,1]]
    #卷积 矩阵操作 axis=1 第二维度 行操作；axis=0第一纬度 列操作
    cx = ndimage.filters.convolve1d(Igs,m1,mode='constant',axis=1)
    cy = ndimage.filters.convolve1d(Igs,m1,mode='constant',axis=0)
    cxx = ndimage.filters.convolve1d(Igs,m2,mode='constant',axis=1)
    cyy = ndimage.filters.convolve1d(Igs,m2,mode='constant',axis=0)
    cxy = ndimage.filters.convolve(Igs,m3,mode='constant')
    Eterm=np.zeros([row,col])#初始化数组大小
    for i in range(0,row):
        for j in range(0,col):
            Eterm[i,j] =(cyy[i,j]*cx[i,j]**2 + cxx[i,j]*cy[i,j]**2 -2*cxy[i,j]*cx[i,j]*cy[i,j])/((1+cx[i,j]**2+cy[i,j]**2)**1.5)

    #计算外部力
    Eext = wl*Eline + we*Eedge + wt*Eterm;
    fy, fx = np.gradient(Eext);

    #计算五对角状矩阵
    xs = x.copy()
    ys = y.copy()
    m= xs.shape[0]
    mm,nn = fx.shape

    b=np.zeros([5,])
    b[0]=beta
    b[1]=-(alpha + 4*beta)
    b[2]=(2*alpha + 6*beta) #b(i) 表示v(i)系数，从(i-2)到(i+2)
    b[3]=b[1];
    b[4]=b[0];

    A = b[0]*circshift(np.eye(m),2);
    A = A + b[1]*circshift(np.eye(m),1);
    A = A + b[2]*circshift(np.eye(m),0);
    A = A + b[3]*circshift(np.eye(m),-1);
    A = A + b[4]*circshift(np.eye(m),-2);

    ##计算矩阵A+γI逆
    LU=linalg.lu(A+gama*np.eye(m),permute_l=True)
    L=LU[0]
    U=LU[1]
    Ainv=linalg.inv(U)@linalg.inv(L)

    for i in range(0,NIter):
        #限制边界条件，约束点一直在图像里
        xs[xs<0] = 0
        ys[ys<0] = 0
        xs[xs>(col-1)] = col - 1
        ys[ys>(row-1)] = row - 1
        #迭代计算xt=(A+γI)inv@(x(t-1)-fx(x(t-1),y(t-1)));yt同理
        ssx = gama*xs - kappa*ndimage.map_coordinates(fx,[ys,xs]);#fx中插值计算出[xs,ys]的点
        ssy = gama*ys - kappa*ndimage.map_coordinates(fy,[ys,xs]);
        xs = Ainv@ssx;
        ys = Ainv@ssy;

    return Igs,[x,y],[np.concatenate((xs,[xs[0]])),np.concatenate((ys,[ys[0]]))]

总结

此算法核心思想是一样的，通过不同方法实现，在这个过程中也意识到了很多narray和matlab矩阵的区别，以及一些函数的区别，比如ndimage.map_coordinates和interp2的插值区别，当然numpy中也有Matrix矩阵，在这个地方没有用是因为觉得numpy功能还是更强大一些哈哈哈，虽然可能这个强大并没有用到，初学python和matlab，在这个改写的过程中学到了很多，另外，后来我发现了一个Python的skimage和Matlab的Active Contour Segmentation可以直接调用，但还没有进行深入研究，待研究后更新