本节根据置换的和多重线性函数来推导行列式的展开式
0 回忆行列式函数D的性质
(i) 若存在i不等于j有ai= aj 则D(a1,…,an)=0;
(ii)D是其自变量的多重线性函数
(iii)D(e1,…,en)=1;
(iv)若D是其自变量的交错函数,即如果交换ai和aj,则D的值将改变一个因子(-1)
1 行列式函数D的展开式
(1)定义函数D(a1,a2,…,an)是以a1,a2,…,an为列的矩阵的行列式其自变量aj是列向量:
因此函数D满足行列式的性质
(2)根据性质(ii)D是多重线性函数,于是有:
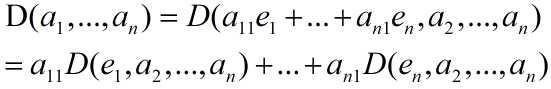
接下来,将a2表示成e1,e2,…,en的线性组合进而得到一个nxn项的公式。上述步骤重复n次可以得到:
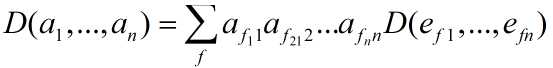
其中的求和号表示从{1,…,n}到{1,…,n}的全体映射ff求和如果f不是置换,则存在i不等于j使得fi = fj 于是根据性质(i)有:
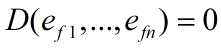
这说明只需对群体置换求和即可。
(3)由于每一个置换都可以分解成对换的乘积根据性质(iv)对D做一次对换,D的值将改变一个因子(-1),
再由置换的性质可知:
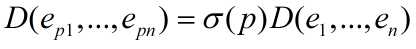
(4)综合上边的式子可以得到:
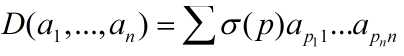
这样就用自变量的分量表示出了D,也就是求出了矩阵行列式的展开式。
(5)矩阵行列式展开式的例子:
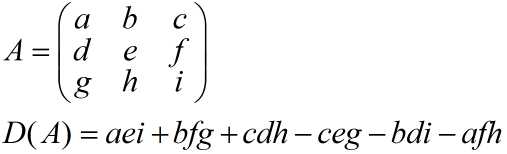
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/37846.html
