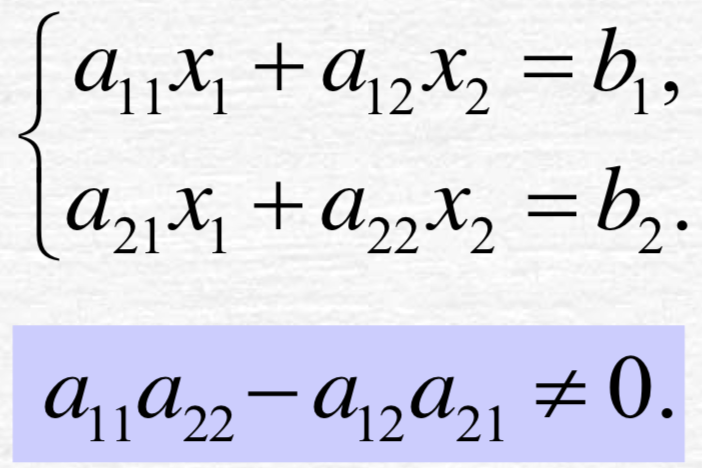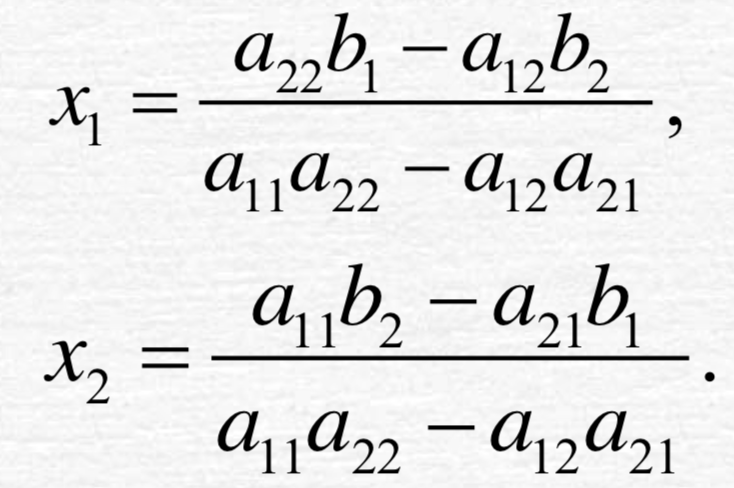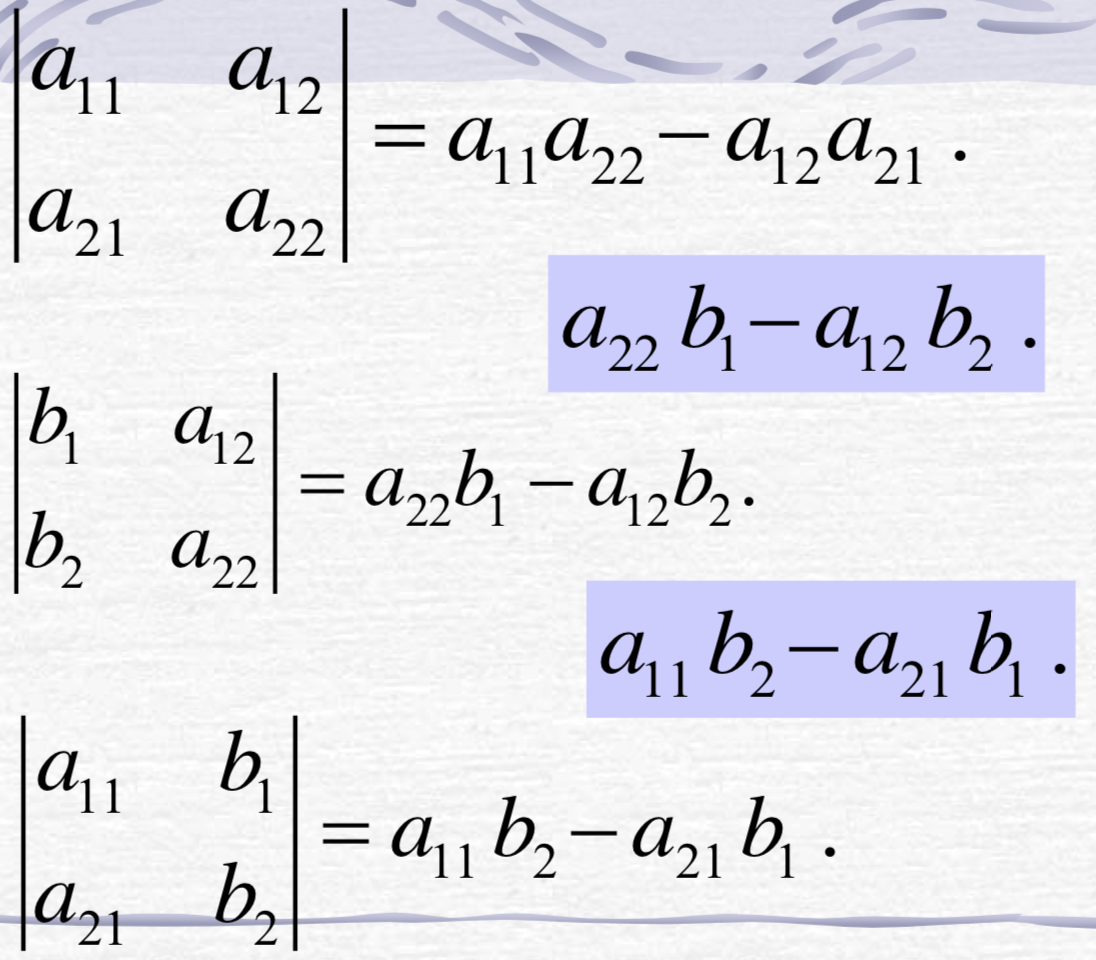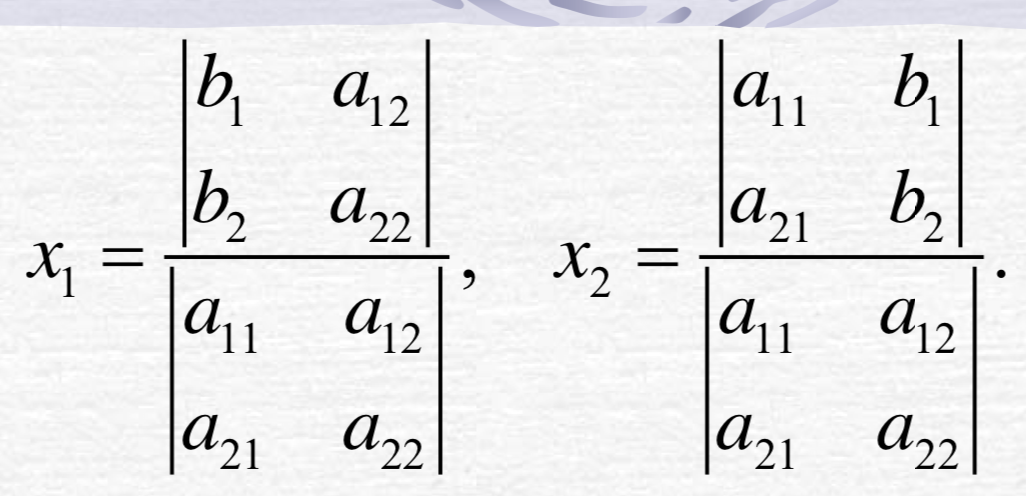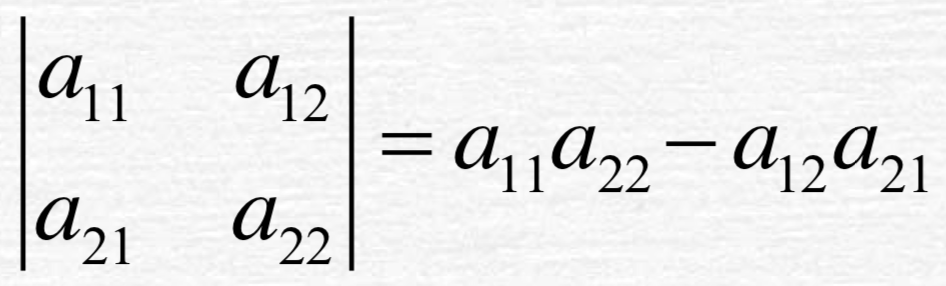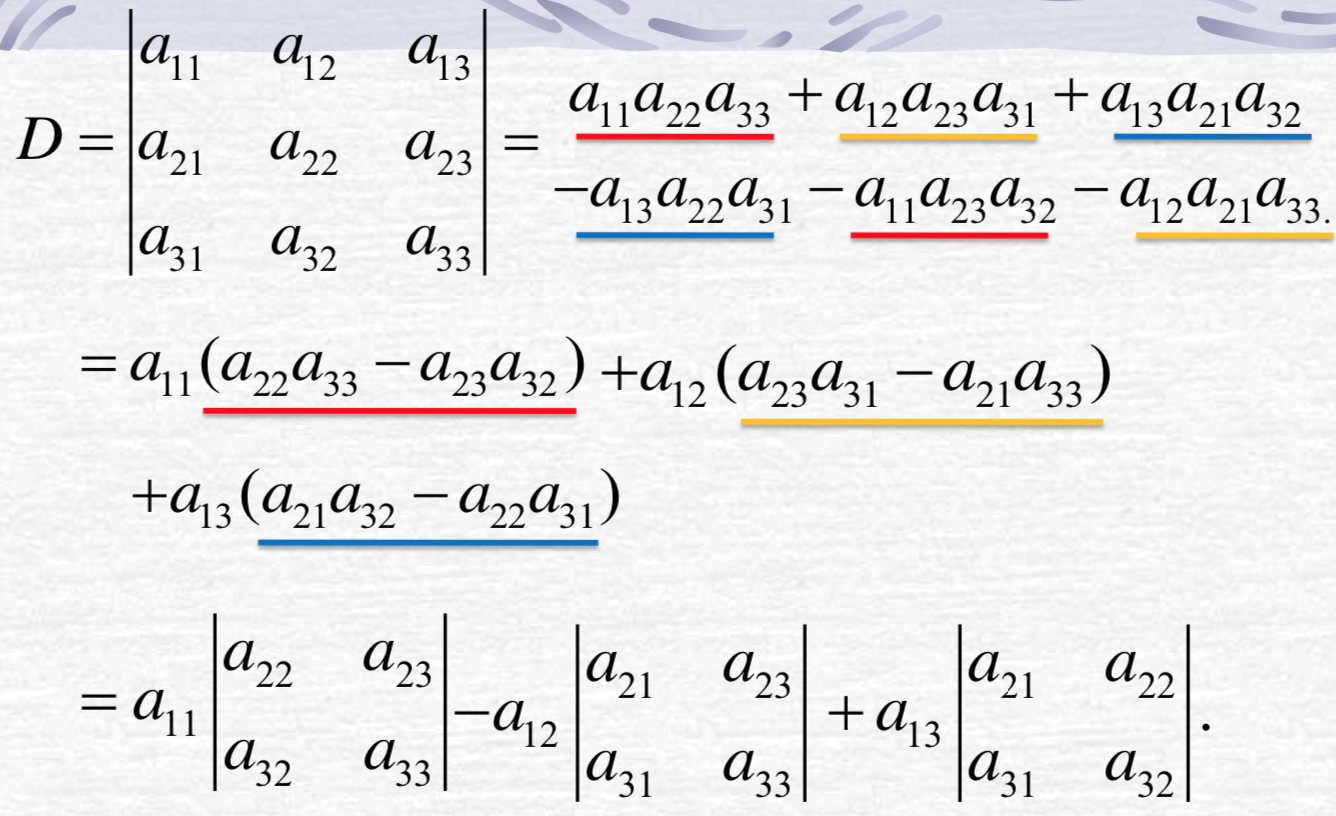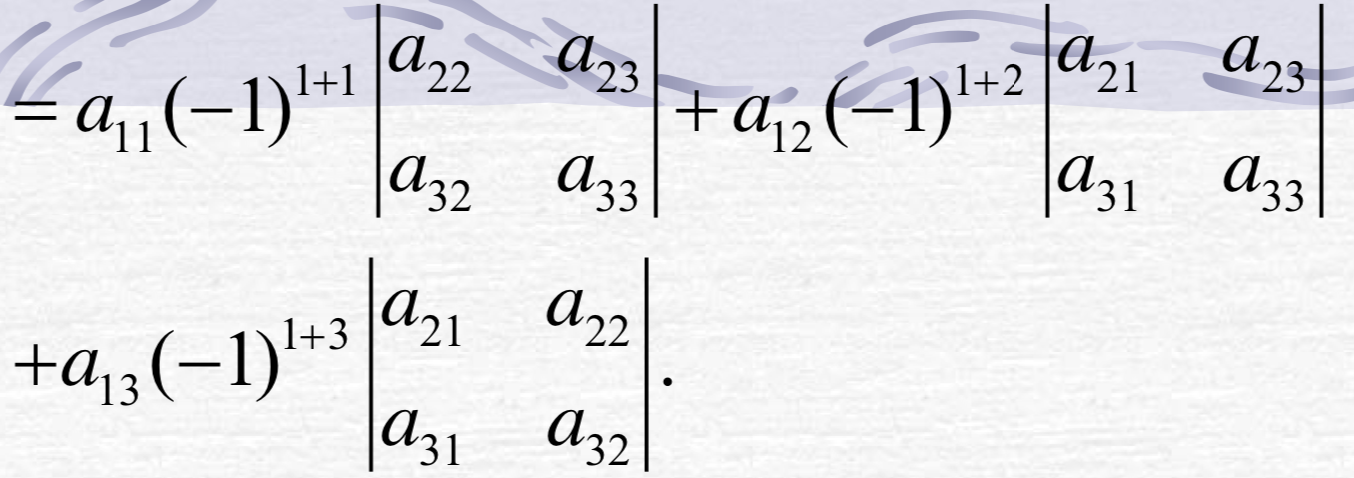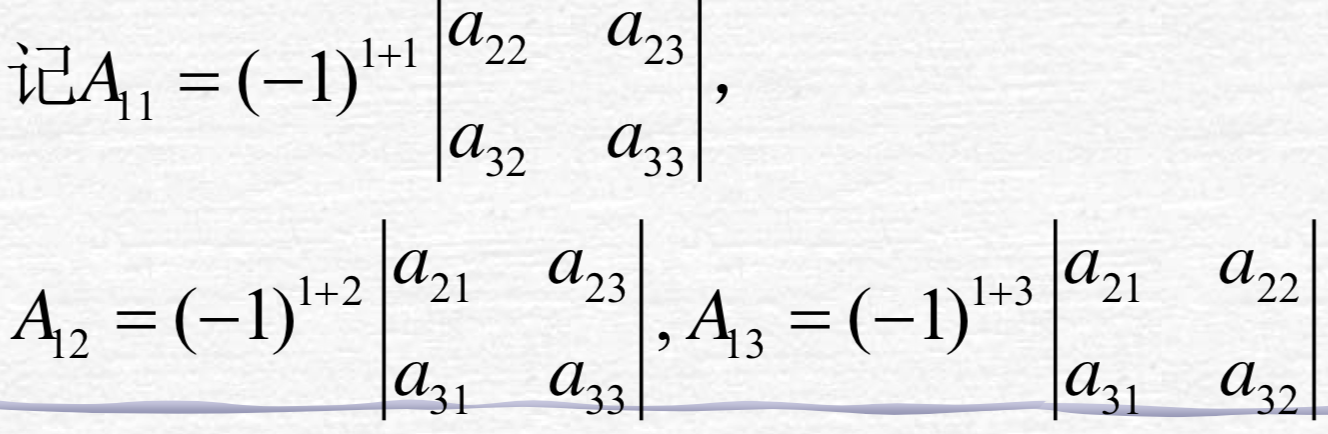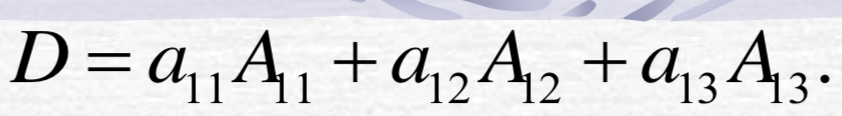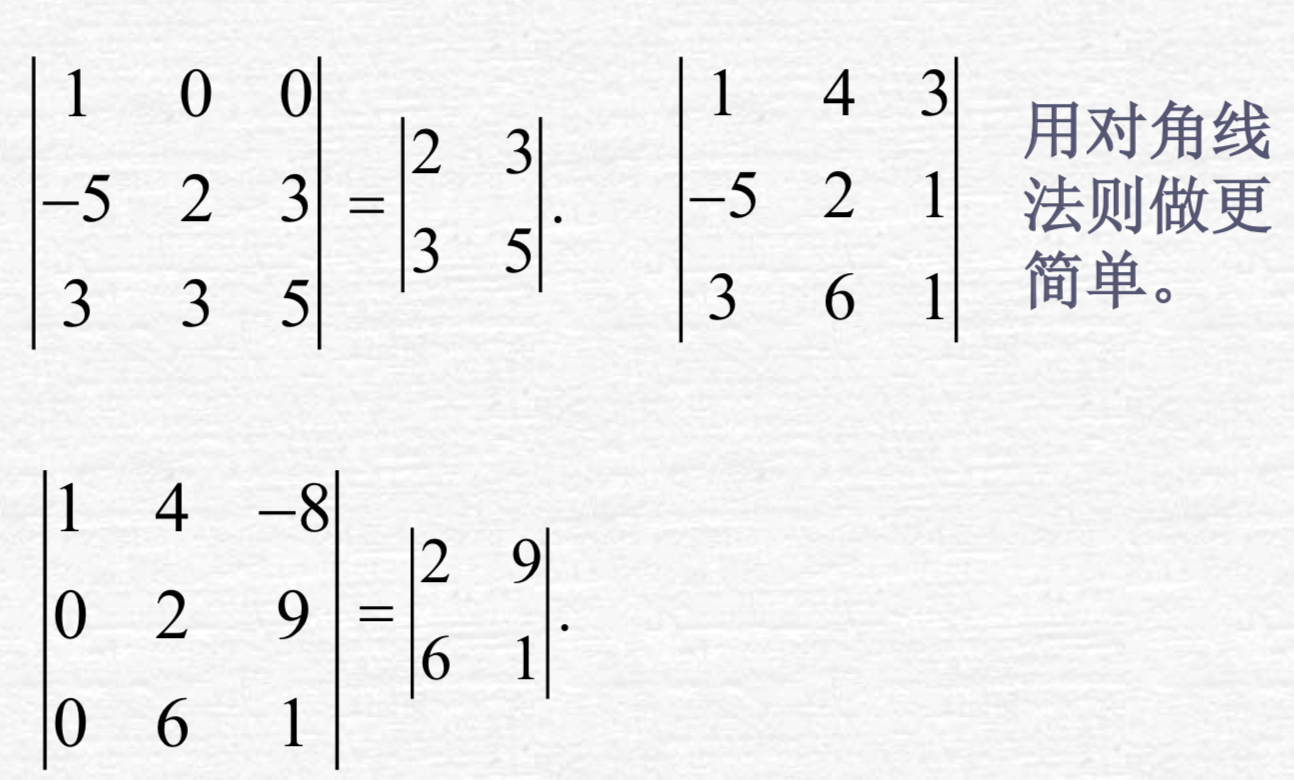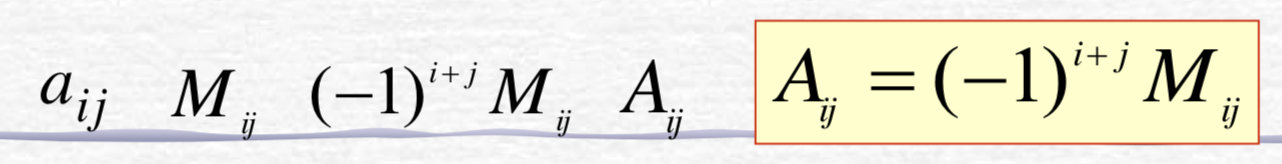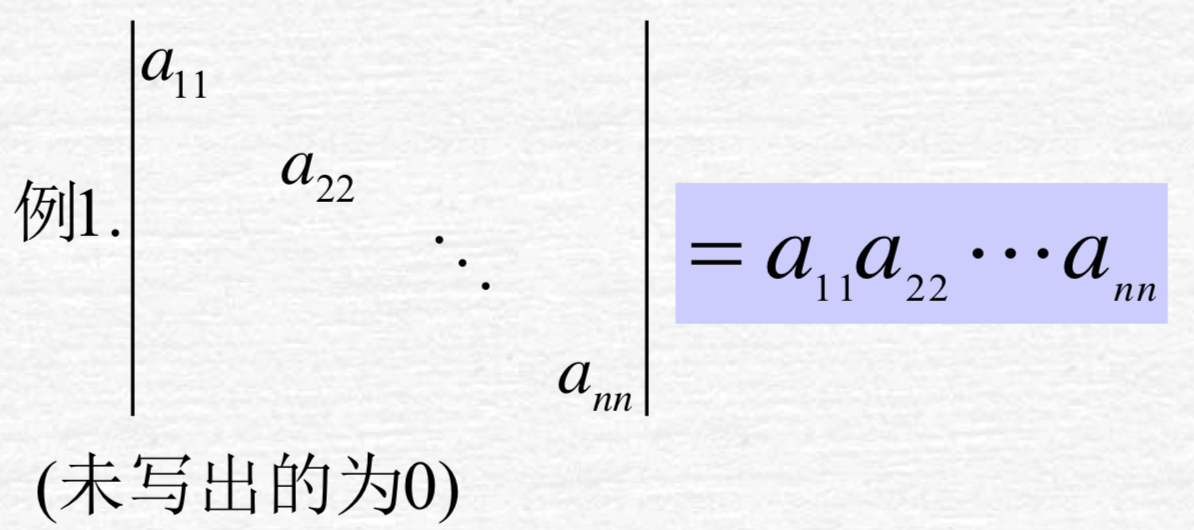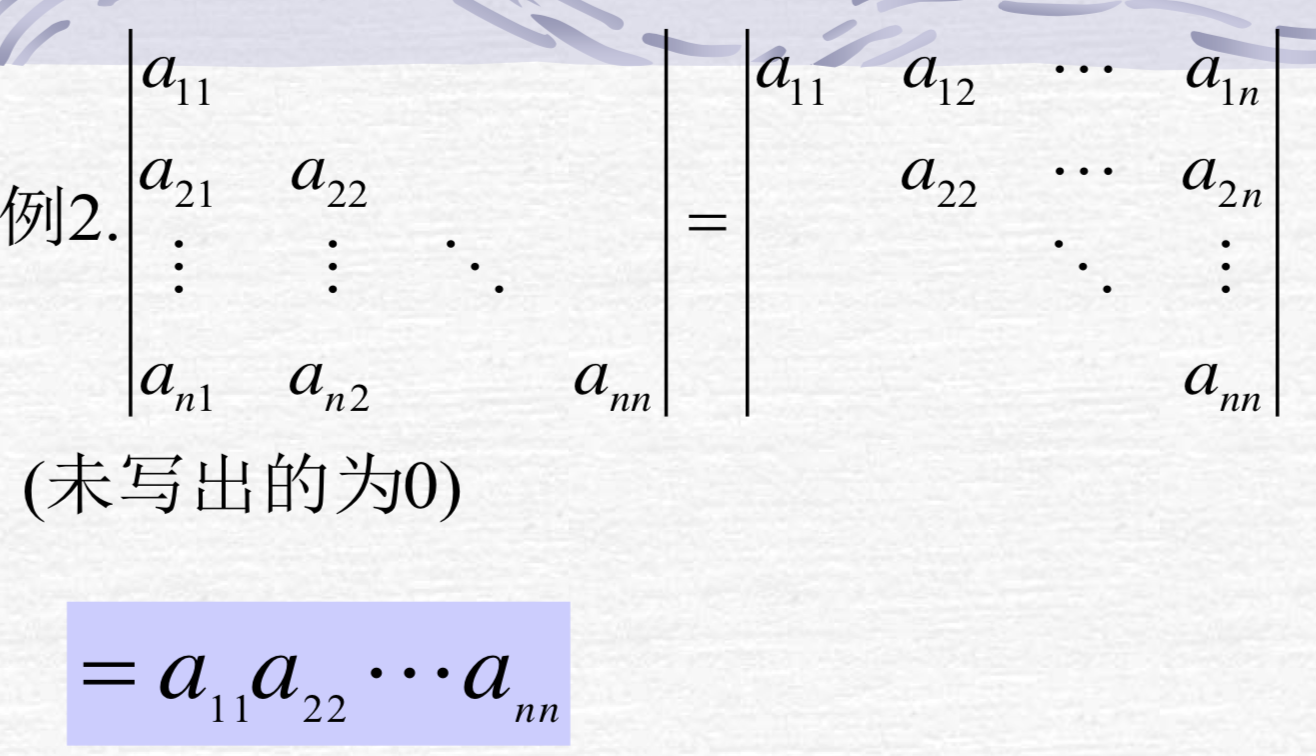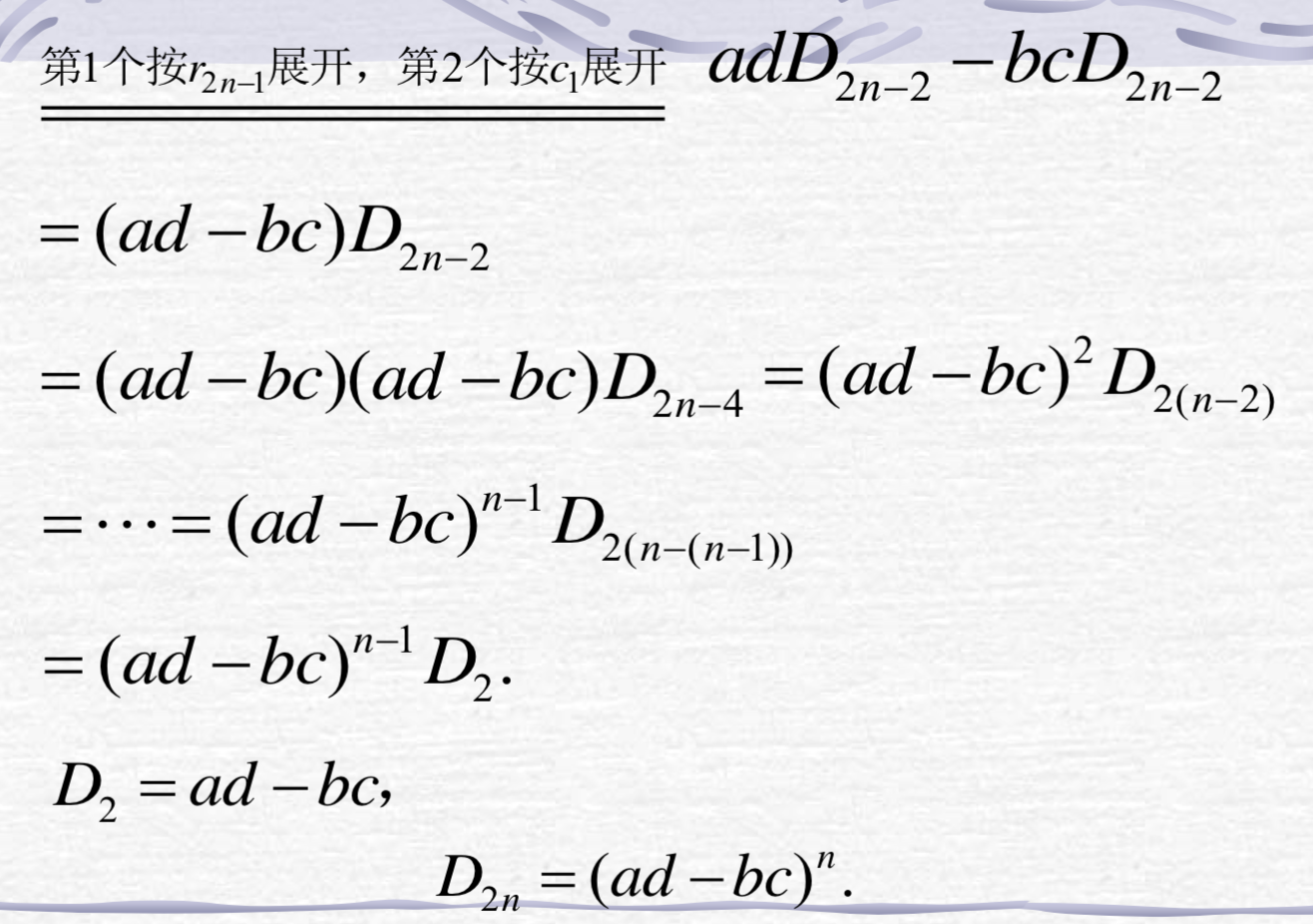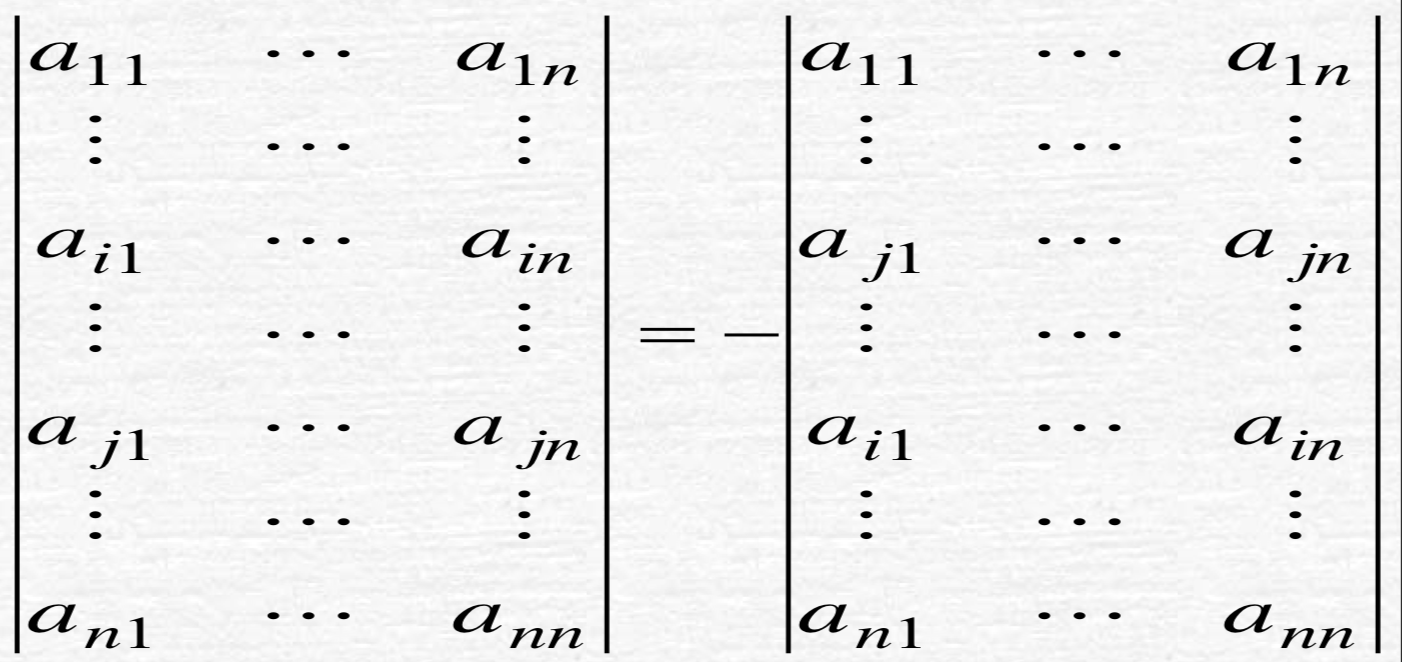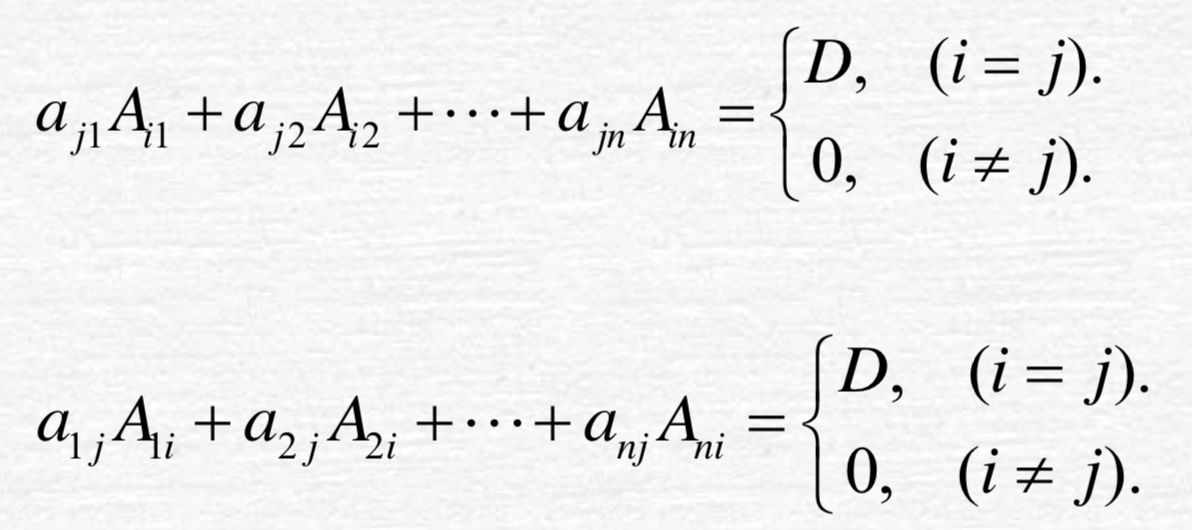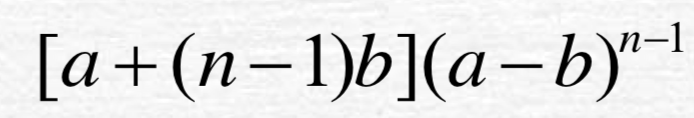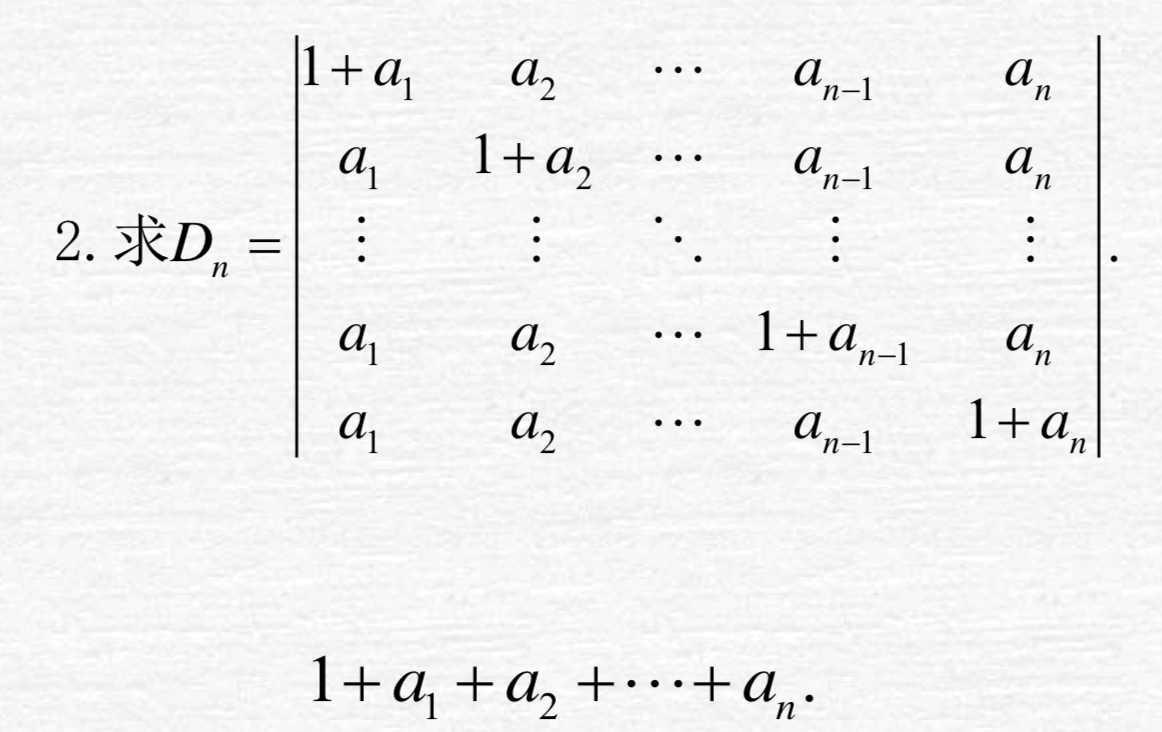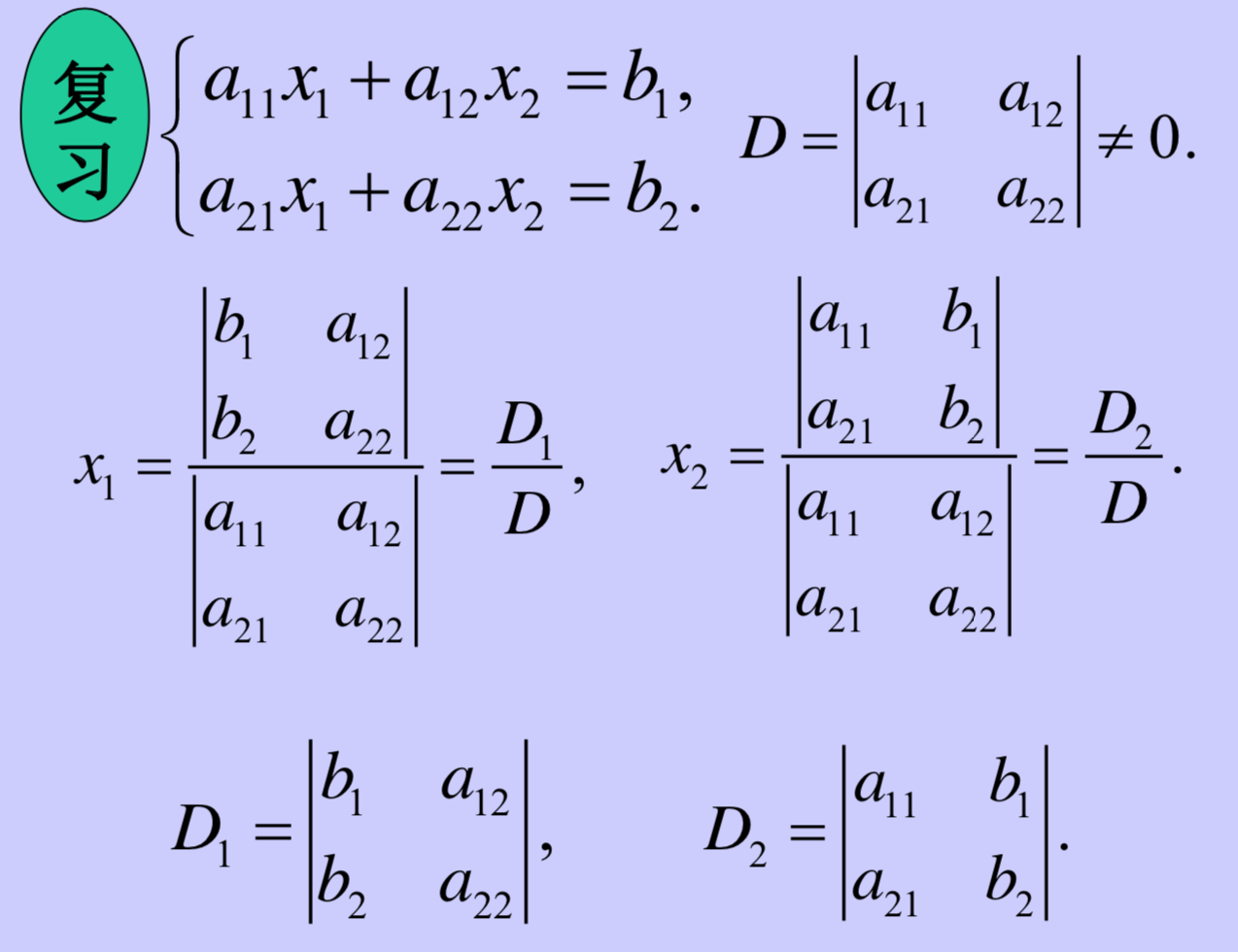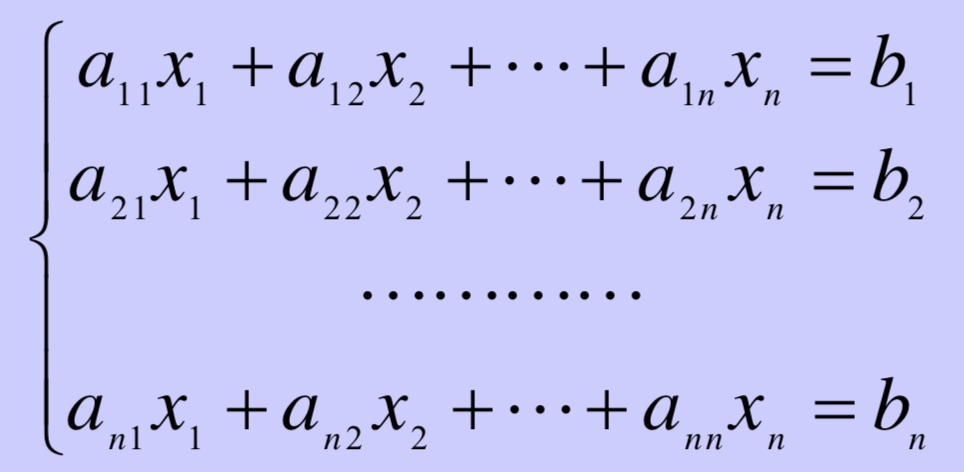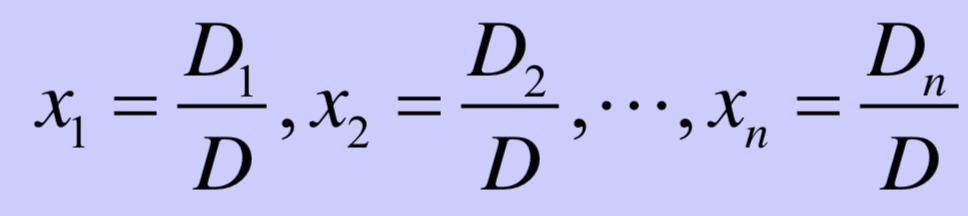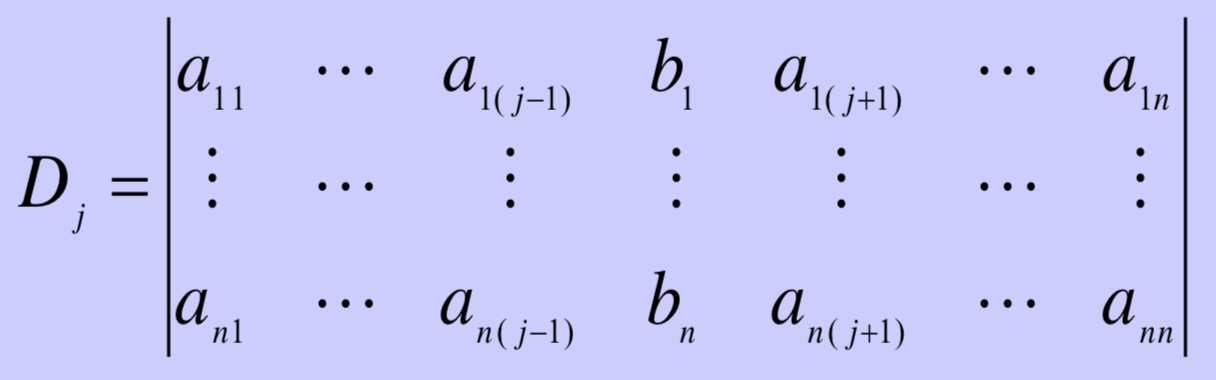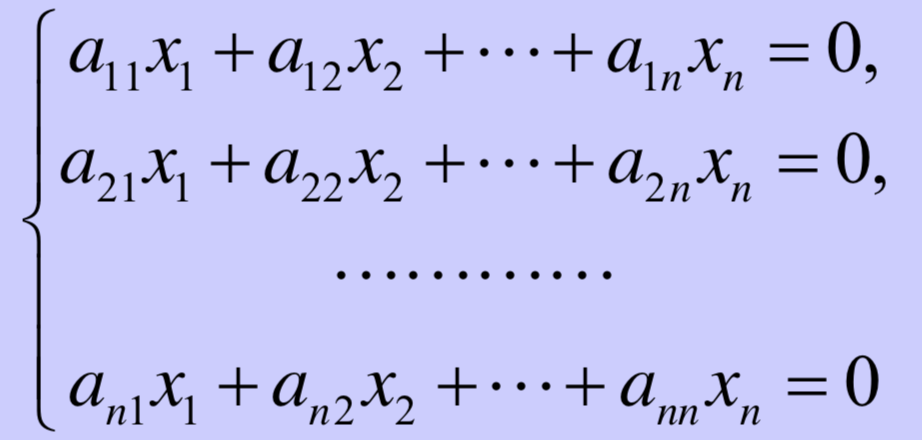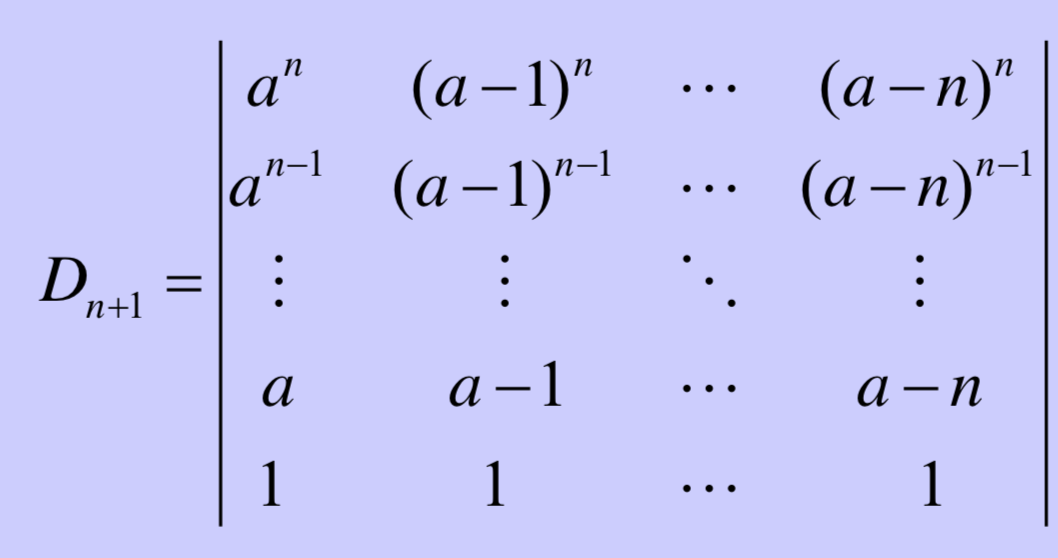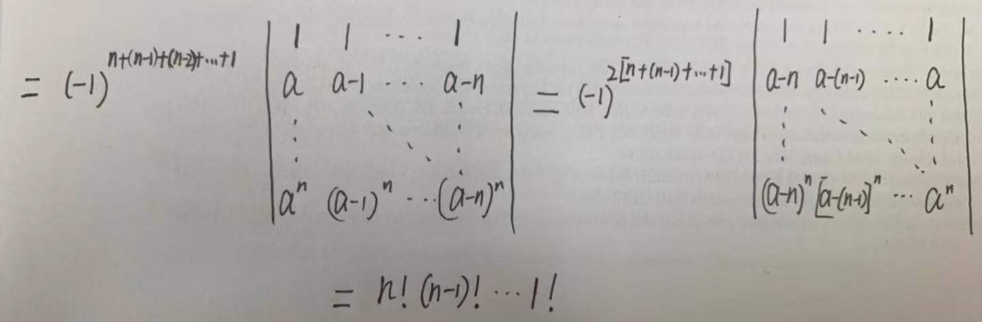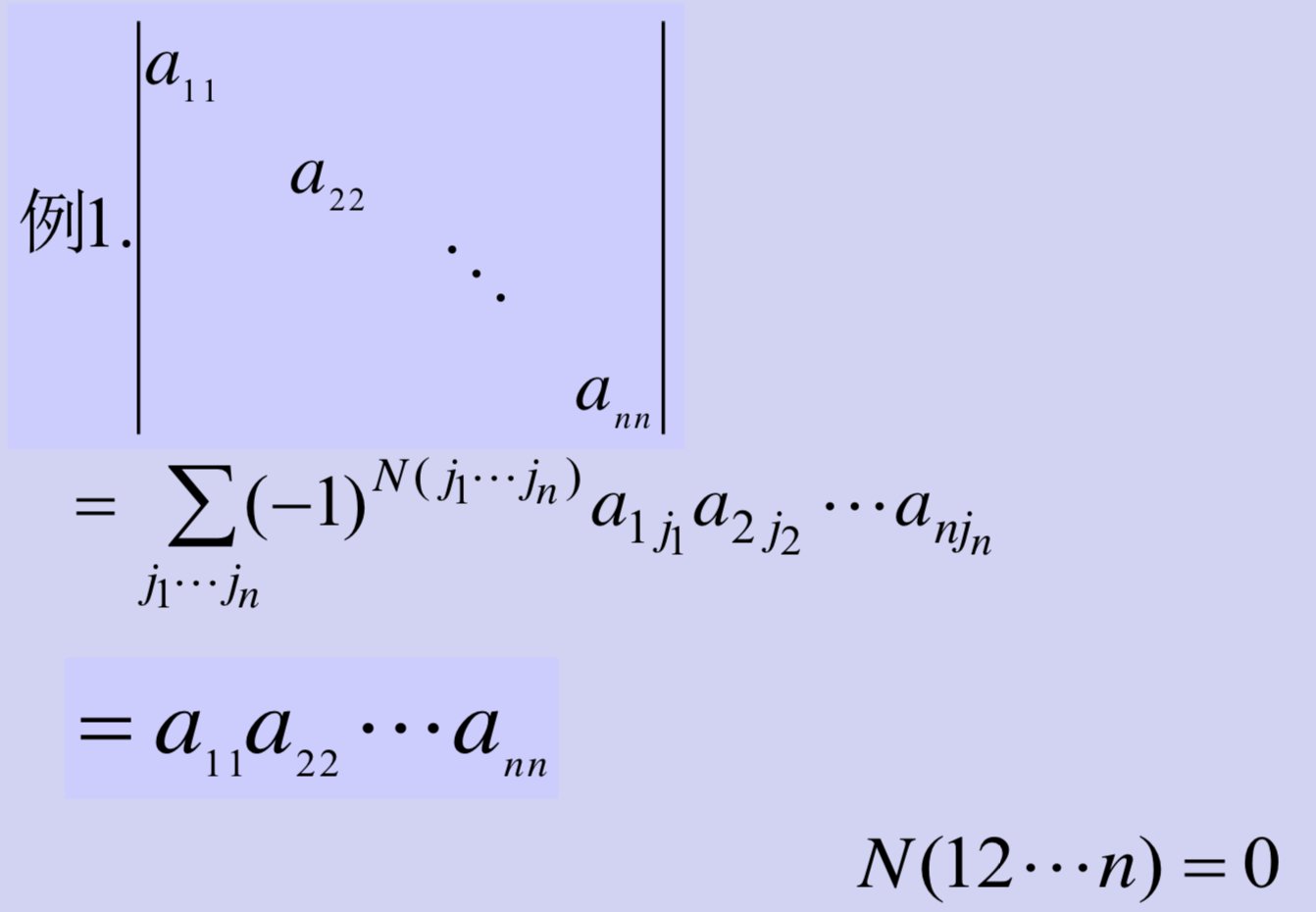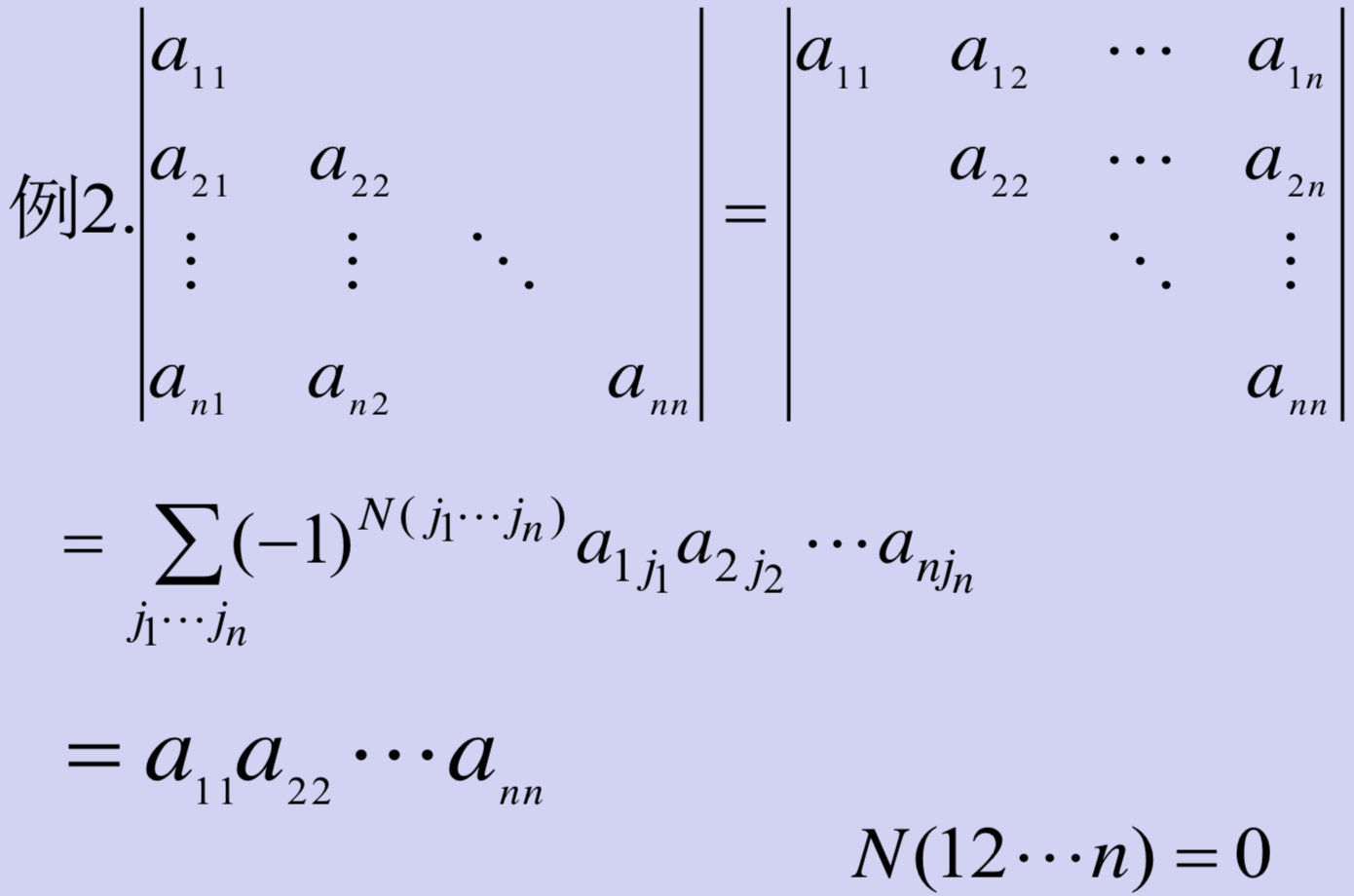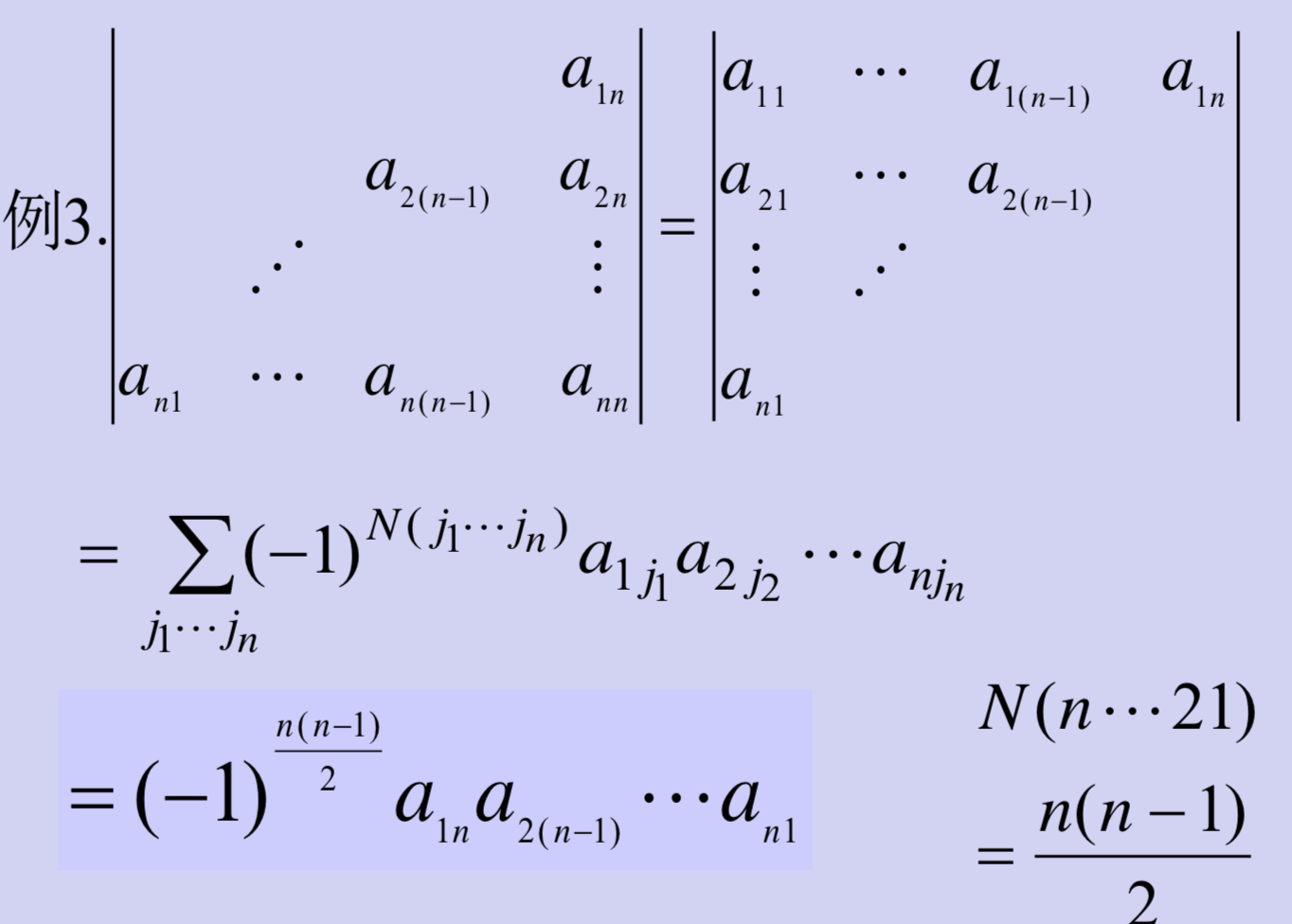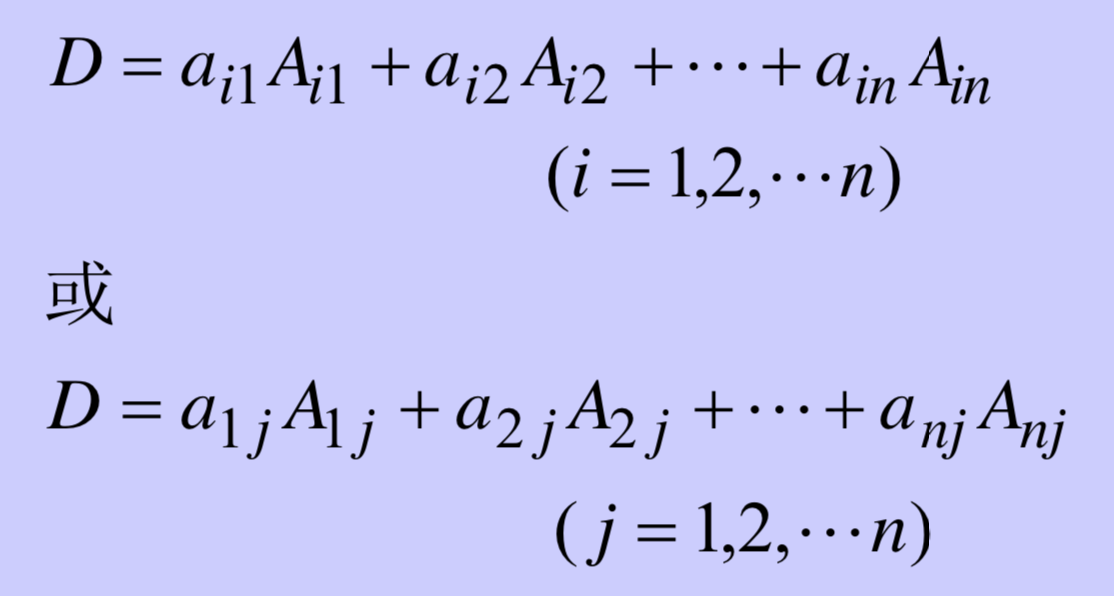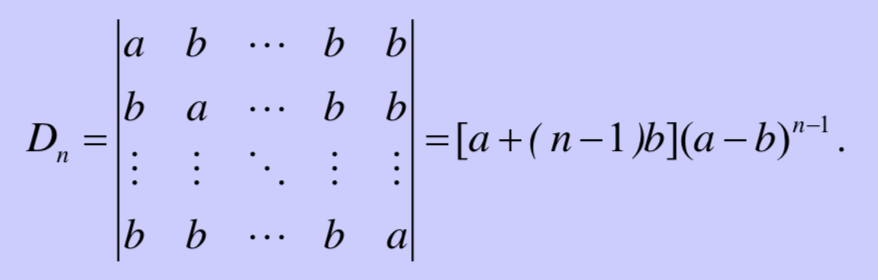线性代数 | (3) 行列式

目录

1. 行列式的概念

2. n阶行列式

3. 特殊行列式的计算

4. 行列式的性质

5. 行列式的计算

6.  克莱姆法则

7. 范德蒙行列式

8. 行列式与逆序数

9. 行列式展开定理

1. 行列式的概念

求下列方程组的解：

利用高斯消元法求解：

为了记忆，引入如下的符号：

下面是给出解的形式：

二阶行列式：

三阶行列式：

2. n阶行列式

这样就可以得到：

类似地，可以按任意一行或列展开：

当计算3阶行列式时，当某一行或列只有一个非零值时，用代数余子式展开会非常好做，不然还是使用之前的对角线法则来做：

• n阶行列式

注意余子式和代数余子式的区别，后者有符号：

一般地，余子式,在原始行列式中去掉第i行、第j列的元素后，剩余元素的行列式，代数余子式是在的基础上再乘以：

n阶行列式的计算可以按行或列展开：

3. 特殊行列式的计算

• 对角行列式

• 三角行列式

包括下三角行列式和上三角行列式：

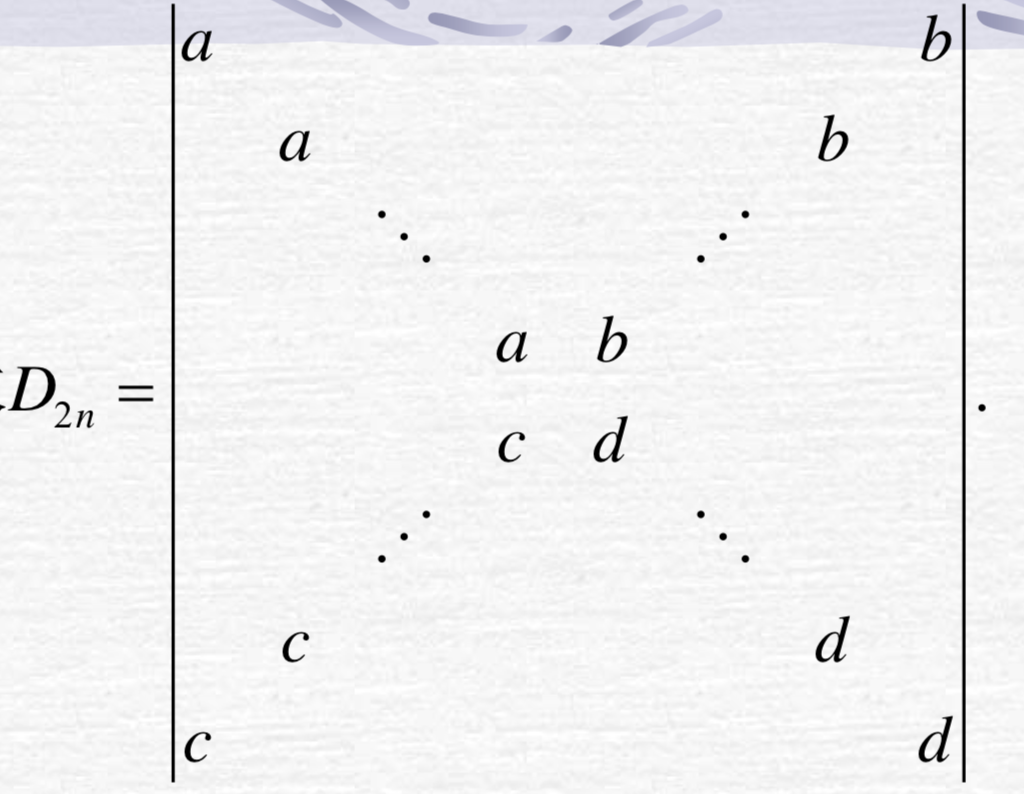
• 斜三角行列式

• 计算下列行列式

按第一列展开：

4. 行列式的性质

• 性质1

  即

在行列式中，行和列的位置是对称的，对行成立的，对列也成立。下面只介绍关于行列式的行的性质。

• 性质2

互换两行，行列式变号：

推论：

若行列式中有两行元素完全相同 则行列式为零（只有0的相反数是本身）。

证明：

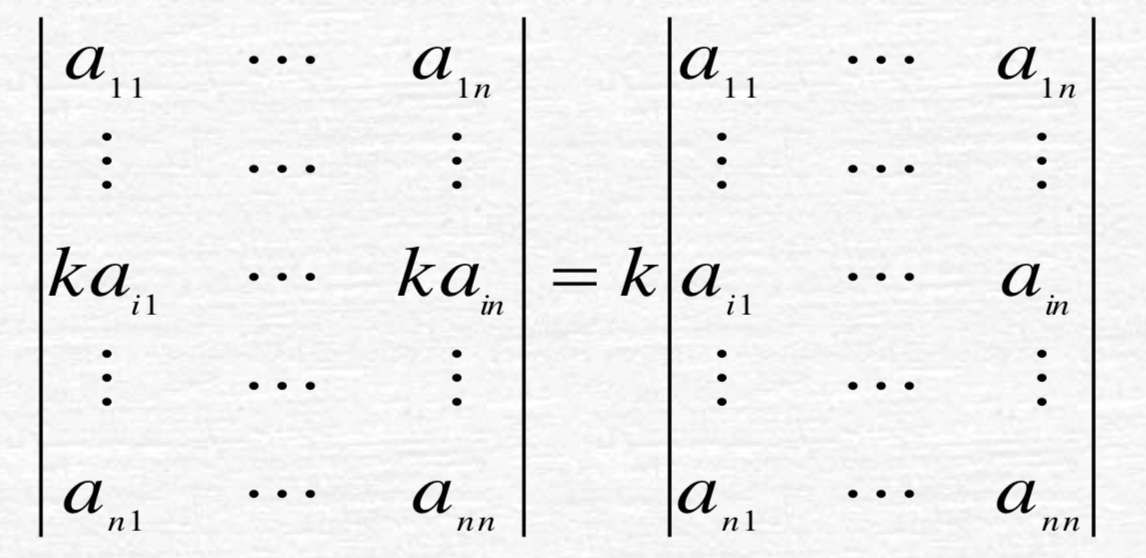
• 性质3

用数k乘行列式某一行中所有元 素，等于用k乘此行列式。即:

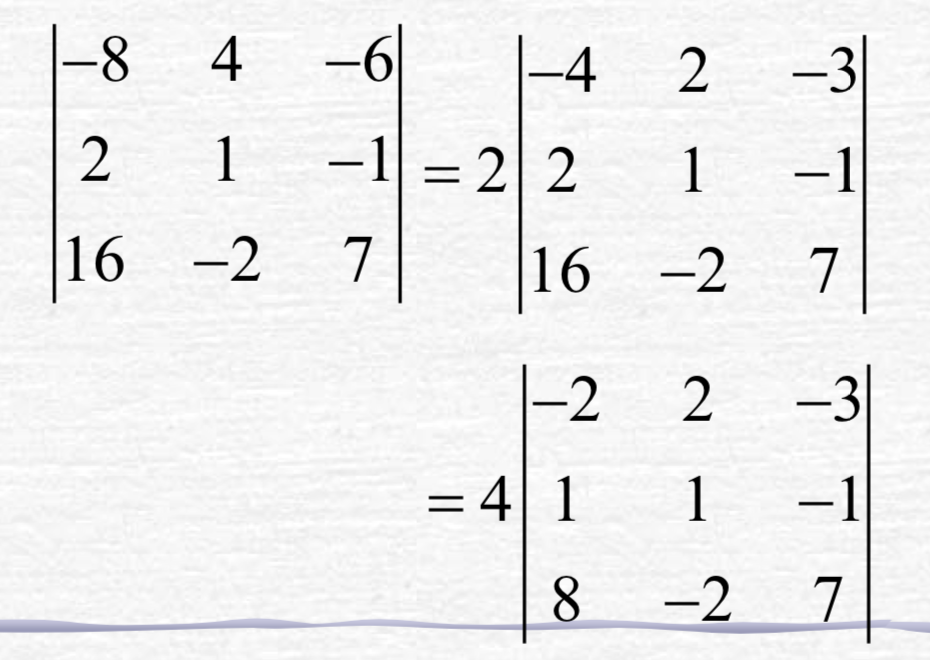
推论：

某一行/列的所有元素的公因子可以 提到行列式符号的外面。

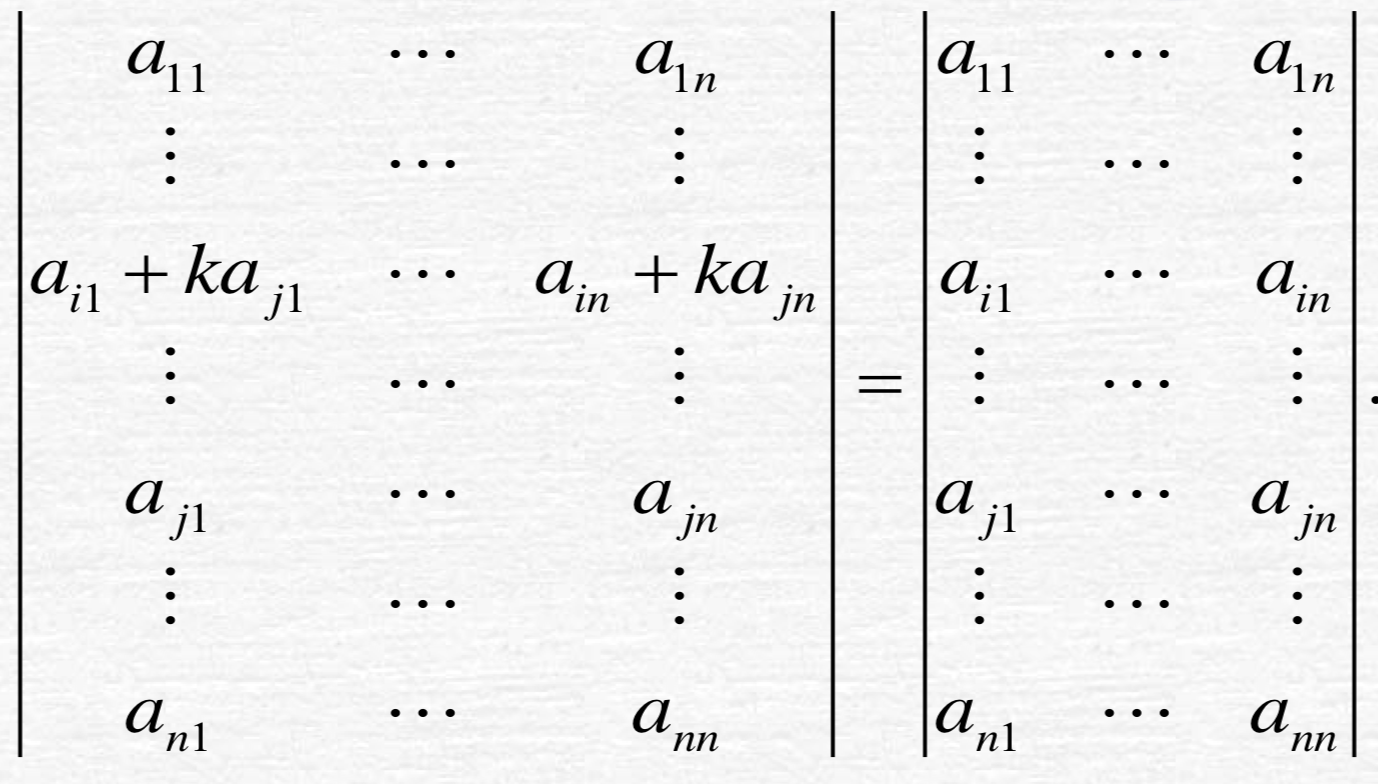
• 性质4

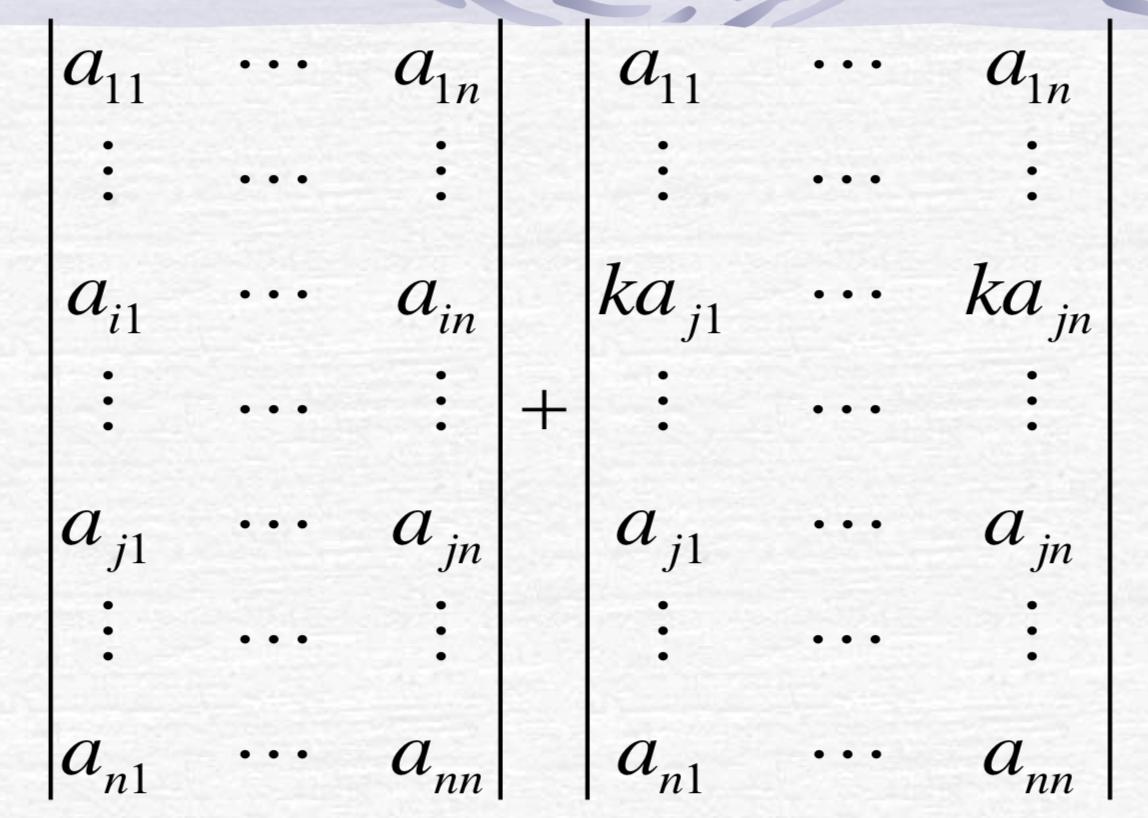
行列式某一行元素加上另 一行对应元素的k倍，行列式的值 不变。即:

证明：

可以把左边行列式拆开，把拆开后的右边提出k后，会发现有两行相同，这一部分为0，所以是不变的：

• 性质5

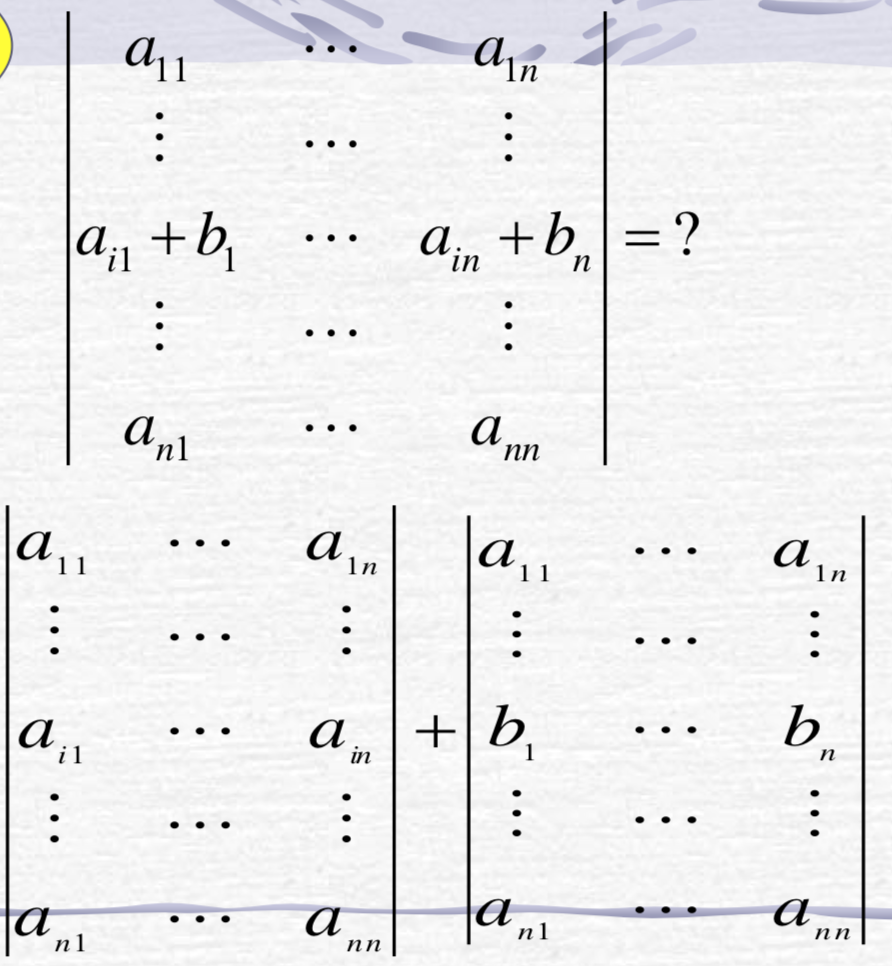
若行列式某一行的元素是两数之 和，则行列式可拆成两个行列式的和。

推论：

若行列式某一行的元素都是m个元素的和，则行列式可以写成m个 行列式的和。

5. 行列式的计算

更一般地：

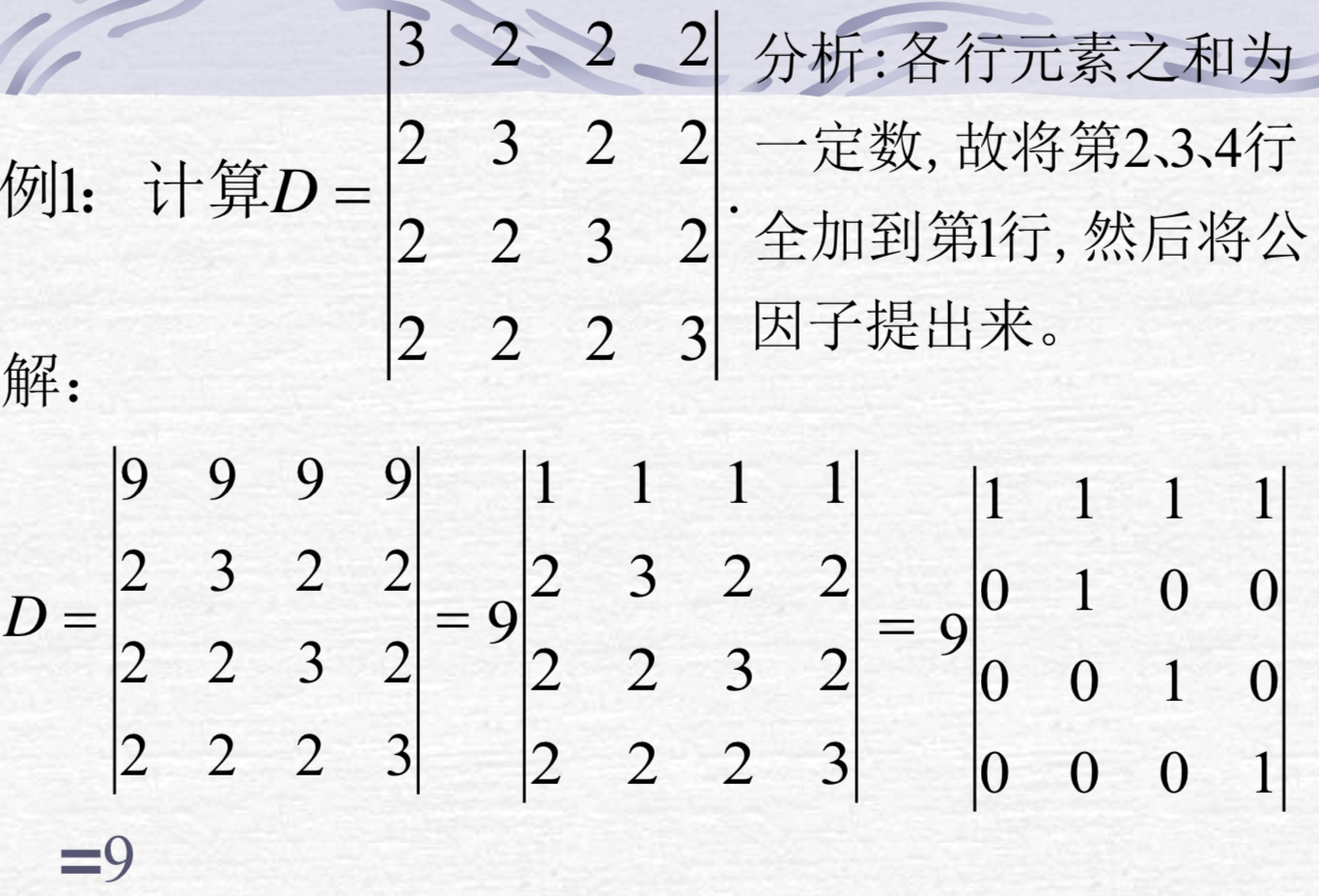
• 练习

如果某行或列全为0的话，则行列式为0.

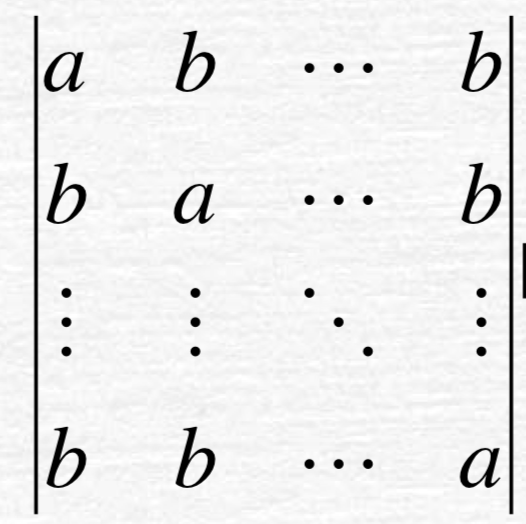
各个行的和是一样的，所以可以把各列加到第一列上，提出因子,分别把第一列的倍加到第j列上，得到一个下三角矩阵。

可以把某行/列的k倍加到另一行/列，使某行或列尽可能出现更多0值，然后按该行/列展开，逐步化简。

6.  克莱姆法则

二元方程组可以使用行列式求解：

n元方程组的解也可以用行列式求解：

• 定理1

若方程组的系数行列式不等于0：

则方程组有惟一解：

• 定理2

下面的方程组被称为奇次线性方程组：

若齐次方程组的系数行列式,则方程组有惟一零解.

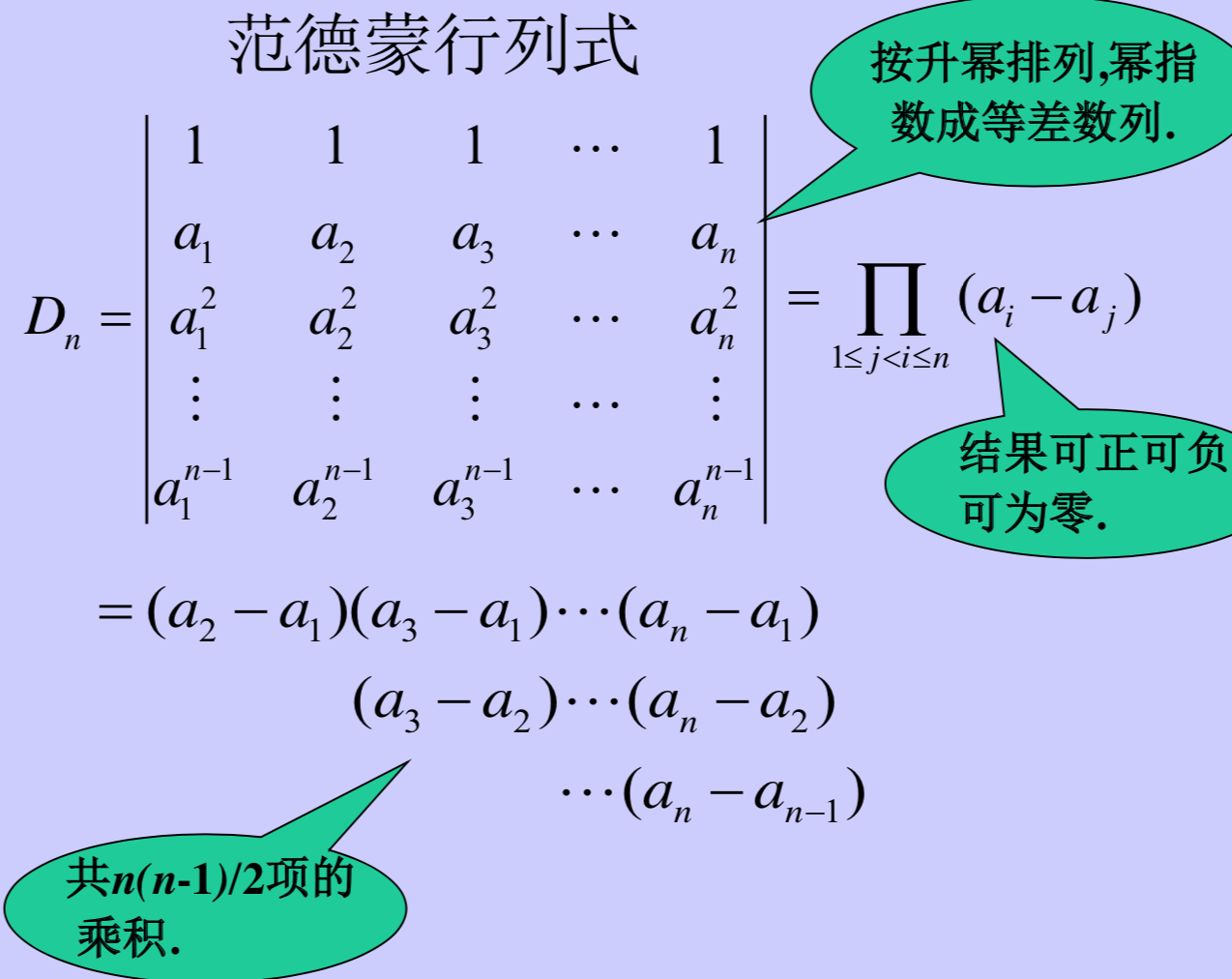
7. 范德蒙行列式

对于降幂排列：

先把降幂转换为升幂，最后一行依次向上移动，其他行同样依次移动；再以同样的方式，移动各个列，把大数放在右边，小数在左边，保证为正数：

8. 行列式与逆序数

• 全排列与逆序数

全排列：

n个不同的元素排成一列，称为n个元素的 全排列。如:12345678，76532184，等等 均为8个元素的全排列。n个元素的全排列共有n!个。

逆序与逆序数：

全排列123 ·n称为标准排列,此时元素之间的顺序称为标准顺序。在任一排列中，若某两个元素的顺序与标准顺序不 同，就称这两个元素构成了一个逆序。213中，2与1就构成了一 个逆序。321中，1与2， 2与3，1与3都构成逆序。

在一个排列中，逆序的总和称为逆序 数。如213的逆序数为1，321的逆序 数为3。

从第一个元素起，该元素前 有几个数比它大，这个元素的逆序就 是几。将所有元素的逆序相加，即得到排列的逆序数。

• 练习

• 逆序数为奇数的排列称为奇排列，逆 序数为偶数的排列称为偶排列。如

在三个元素的全排列中，123、231、312为偶排列，逆序数分别为0、2、2；132、213、321为奇排列，逆序数分别为1、1、3.

• 对换

在一个排列中，任意对调两个元素， 其余元素不变，即得到一个新排列， 这样一种变换称为对换。

性质：

1) 任意一个排列经过一次对换后，奇偶性改变。

2）在n个元素的全排列中，奇偶排列各占一半 n!/2.

• 三阶行列式

• n阶行列式

9. 行列式展开定理

n阶行列式D 等于它的任一行(列)各 元素与其对应的代数余子式乘积之和,即