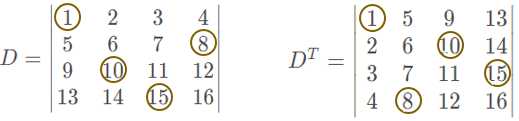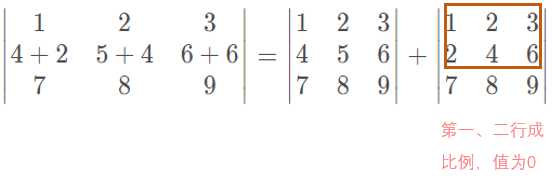行列式的展开形式
上一篇文章中,我们提到过行列式的按行展开:
行标始终取为标准排列,列标取遍排列的所有可能,从不同行不同列取出n个元素相乘,其符号由列标排列的奇偶性决定。
行列式除了可以按行展开,还有另外两种展开方式:按列展开和既不按行也不按列展开。
- 按列展开
列标始终取为标准排列,行标取遍排列的所有可能,从不同行不同列取出n个元素相乘,其符号由行标排列的奇偶性决定。
例如下面这个三阶行列式,按列展开为:
∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ = a 11 a 22 a 33 − a 11 a 32 a 23 − a 21 a 12 a 33 + a 21 a 32 a 13 + a 31 a 12 a 23 − a 31 a 22 a 13 = ① − ② − ③ + ④ + ⑤ − ⑥ \begin{aligned}\begin{vmatrix}a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix}&=a_{11} a_{22}a_{33} -a_{11} a_{32} a_{23}-a_{21} a_{12}a_{33}+a_{21}a_{32}a_{13}+a_{31}a_{12}a_{23}-a_{31}a_{22}a_{13} \\&= \ \ \ \ \ \ \ ①\ \ \ \ \ \ -\ \ \ \ \ \ ②\ \ \ \ \ \ -\ \ \ \ \ \ ③\ \ \ \ \ \ +\ \ \ \ \ \ ④\ \ \ \ \ \ +\ \ \ \ \ \ ⑤\ \ \ \ \ \ -\ \ \ \ \ \ ⑥\end{aligned} ∣∣∣∣∣∣a11a21a31a12a22a32a13a23a33∣∣∣∣∣∣=a11a22a33−a11a32a23−a21a12a33+a21a32a13+a31a12a23−a31a22a13= ① − ② − ③ + ④ + ⑤ − ⑥
观察展开式中的每一项,我们可以得到如下结果:
| 第 i 项 | 符号 | 行 标 | 列 标 | 行标的逆序数 |
|---|---|---|---|---|
| ① | + | 123 | 123 | 0(偶排列) |
| ② | – | 132 | 123 | 1(奇排列) |
| ③ | – | 213 | 123 | 1(奇排列) |
| ④ | + | 231 | 123 | 2(偶排列) |
| ⑤ | + | 312 | 123 | 2(偶排列) |
| ⑥ | – | 321 | 123 | 3(奇排列) |
与前面我们所学习过的按行展开的行列式对比,我们可以发现,其结果是一致的,只是顺序有调换。
对于 n \ n n阶行列式,按列展开的一般形式可以写作:
∣ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ∣ = ∑ i 1 , i 2 , ⋯ , i n ( − 1 ) N ( i 1 i 2 ⋯ i n ) a i 1 1 a i 2 2 ⋯ a i n n \begin{vmatrix}a_{11} & a_{12}& \cdots&a_{1n}\\a_{21} & a_{22}&\cdots& a_{2n}\\\vdots &\vdots& \ddots&\vdots\\ a_{n1} & a_{n2}& \cdots&a_{nn}\end{vmatrix}=\sum_{i_1,i_2,\cdots,i_n}(-1)^{N(i_1i_2 \cdots i_n)} a_{i_11}a_{i_22} \cdots a_{i_nn} ∣∣∣∣∣∣∣∣∣a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1na2n⋮ann∣∣∣∣∣∣∣∣∣=i1,i2,⋯,in∑(−1)N(i1i2⋯in)ai11ai22⋯ainn
- 既不按行也不按列展开
与前两种展开方式区别,这种展开方式的列标和行标都不取为标准排列。从不同行不同列取出n个元素相乘,其符号由行标排列与列标排列的和的奇偶性决定。
对于 n \ n n阶行列式,既不按行也不按列展开的一般形式可以写作:
∣ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ∣ = ∑ ( − 1 ) N ( i 1 i 2 ⋯ i n ) + N ( j 1 j 2 ⋯ j n ) a i 1 j 1 a i 2 j 2 ⋯ a i n j n \begin{vmatrix}a_{11} & a_{12}& \cdots&a_{1n}\\a_{21} & a_{22}&\cdots& a_{2n}\\\vdots &\vdots& \ddots&\vdots\\ a_{n1} & a_{n2}& \cdots&a_{nn}\end{vmatrix}=\sum_{}(-1)^{N(i_1i_2 \cdots i_n)+N(j_1j_2 \cdots j_n)} a_{i_1j_1}a_{i_2j_2} \cdots a_{i_nj_n} ∣∣∣∣∣∣∣∣∣a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1na2n⋮ann∣∣∣∣∣∣∣∣∣=∑(−1)N(i1i2⋯in)+N(j1j2⋯jn)ai1j1ai2j2⋯ainjn
我们可以将三种展开方式做一个对比:
| 展开方式 | 特点 | n阶行列式的一般表示 |
|---|---|---|
| 按行展开 | 行标始终取为标准排列,列标取遍排列的所有可能,从不同行不同列取出n个元素相乘,其符号由列标排列的奇偶性决定。 | ∑ j 1 , j 2 , ⋯ , j n ( − 1 ) N ( j 1 j 2 ⋯ j n ) a 1 j 1 a 2 j 2 ⋯ a n j n \sum_{j_1,j_2,\cdots,j_n}(-1)^{N(j_1j_2 \cdots j_n)} a_{1j_1}a_{2j_2} \cdots a_{nj_n} ∑j1,j2,⋯,jn(−1)N(j1j2⋯jn)a1j1a2j2⋯anjn |
| 按列展开 | 列标始终取为标准排列,行标取遍排列的所有可能,从不同行不同列取出n个元素相乘,其符号由行标排列的奇偶性决定。 | ∑ i 1 , i 2 , ⋯ , i n ( − 1 ) N ( i 1 i 2 ⋯ i n ) a i 1 1 a i 2 2 ⋯ a i n n \sum_{i_1,i_2,\cdots,i_n}(-1)^{N(i_1i_2 \cdots i_n)} a_{i_11}a_{i_22} \cdots a_{i_nn} ∑i1,i2,⋯,in(−1)N(i1i2⋯in)ai11ai22⋯ainn |
| 既不按行也不按列展开 | 列标和行标都不取为标准排列。从不同行不同列取出n个元素相乘,其符号由行标排列与列标排列的和的奇偶性决定。 | ∑ ( − 1 ) N ( i 1 i 2 ⋯ i n ) + N ( j 1 j 2 ⋯ j n ) a i 1 j 1 a i 2 j 2 ⋯ a i n j n \sum_{}(-1)^{N(i_1i_2 \cdots i_n)+N(j_1j_2 \cdots j_n)} a_{i_1j_1}a_{i_2j_2} \cdots a_{i_nj_n} ∑(−1)N(i1i2⋯in)+N(j1j2⋯jn)ai1j1ai2j2⋯ainjn |
小练习
讨论行列式展开式中某一项: ( − 1 ) N ( i 21 m ) + N ( 1 k 32 ) a i 1 a 2 k a 13 a m 2 (-1)^{N(i21m)+N(1k32)}a_{i1}a_{2k}a_{13}a_{m2} (−1)N(i21m)+N(1k32)ai1a2ka13am2的符号为正还是为负。
思路:1) 观察该项,首先判断该展开式采用哪一种展开方式。从两个排列 i 21 m i21m i21m 和 1 k 32 1k32 1k32,可以看出他的列标和行标都不取为标准排列,因此属于既不按行排列,也不按列排列;
2) 元素 a i 1 a_{i1} ai1、 a 2 k a_{2k} a2k、 a 13 a_{13} a13和 a m 2 a_{m2} am2分别来自不同行和不同列。所以 k = 4 , i = 3 k=4,i=3 k=4,i=3 或 4 ; m = 4 \ 4;m=4 4;m=4 或 3 \ 3 3;
3) 再根据两个排列的逆序数之和,判断出其符号。
行列式的转置
行列式的转置即:把行列式原来的行变作列(原来的列变作行)。如果把行列式记作 D D D,那么行列式的转置记作 D T D^T DT。
以三阶行列式为例:
我们可以发现, ( D T ) T = D (D^T)^T=D (DT)T=D。
小练习
求 D = ∣ 1 2 3 1 1 1 8 8 8 ∣ D=\begin{vmatrix}1 & 2 & 3 \\1 & 1 &1 \\8 & 8 & 8 \end{vmatrix} D=∣∣∣∣∣∣118218318∣∣∣∣∣∣的转置和转置的转置。
解: D T = ∣ 1 2 3 1 1 1 8 8 8 ∣ D^T=\begin{vmatrix}1 & 2 & 3 \\1 & 1 &1 \\8 & 8 & 8 \end{vmatrix} DT=∣∣∣∣∣∣118218318∣∣∣∣∣∣ ( D T ) T = ∣ 1 2 3 1 1 1 8 8 8 ∣ (D^T)^T=\begin{vmatrix}1 & 2 & 3 \\1 & 1 &1 \\8 & 8 & 8 \end{vmatrix} (DT)T=∣∣∣∣∣∣118218318∣∣∣∣∣∣
行列式的性质
- 性质1:行列式转置,行列式的值不变(对行成立,对列也成立)。
一起来看一个例子叭!下图是行列式 D D D和 D D D的转置:
我们按行展开,取出 D D D中的一项(包含数字1、8、10、15),记为 a a a:
a = ( − 1 ) N ( 1423 ) × 1 × 8 × 10 × 15 a=(-1)^{N(1423)}×1×8×10×15 a=(−1)N(1423)×1×8×10×15
相似的,我们要取出 D T D^T DT中同样包含包含数字1、8、10、15的一项,观察 D T D^T DT中这几个数字的行标(1423)和列标(1234),可以推断出其为按列展开,记为 a ′ a’ a′:
a ′ = ( − 1 ) N ( 1423 ) × 1 × 8 × 10 × 15 a’=(-1)^{N(1423)}×1×8×10×15 a′=(−1)N(1423)×1×8×10×15
我们可以发现, a = a ′ a=a’ a=a′。其实,如果我们把 D D D和 D T D^T DT展开项中的元素一一对比,可以发现他们的所有项都是相等的,即 D = D T D=D^T D=DT(前面已经说明了行列式按行展开和按列展开的结果是一样的)。
- 性质2:行列式两行互换,行列式的值变号(展开式的每一项都相差一个负号)。
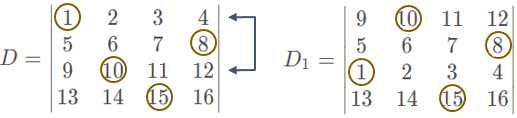
还是通过一个例子来说明!下图是行列式 D D D和进行了两行互换的 D 1 D_1 D1:
我们按行展开,取出 D D D中的一项(包含数字1、8、10、15),记为 a a a:
a = ( − 1 ) N ( 1423 ) × 1 × 8 × 10 × 15 a=(-1)^{N(1423)}×1×8×10×15 a=(−1)N(1423)×1×8×10×15
我们要取出 D 1 D_1 D1中同样包含包含数字1、8、10、15的一项,观察 D 1 D_1 D1中这几个数字的行标(3214)和列标(1423),可以推断出其为既不按行也不按列展开,记为 a ′ a’ a′
a ′ = ( − 1 ) N ( 3214 ) + N ( 1423 ) × 1 × 8 × 10 × 15 a’=(-1)^{N(3214)+N(1423)}×1×8×10×15 a′=(−1)N(3214)+N(1423)×1×8×10×15
我们可以发现, a a a和 a ′ a’ a′的值的区别在于 ( − 1 ) N ( 3214 ) (-1)^{N(3214)} (−1)N(3214)。其实,行列式两行互换,他们的列标不会改变,但行标会交换次序(第一行和第三行互换,行标就由1234变为了3214),因此,两行兑=互换后,结果会多一个负号。 - 推论: 两行(列)相等, D = 0 D=0 D=0。
例如: 对行列式 D = ∣ 1 2 3 4 5 6 7 8 1 2 3 4 13 14 15 16 ∣ D=\begin{vmatrix}1 & 2 & 3& 4 \\5 & 6 &7 & 8 \\1 & 2 & 3 & 4\\13 & 14 & 15&16\end{vmatrix} D=∣∣∣∣∣∣∣∣15113262143731548416∣∣∣∣∣∣∣∣,假如我们交换第一行和第三行,变换成 D ′ = ∣ 1 2 3 4 5 6 7 8 1 2 3 4 13 14 15 16 ∣ D’=\begin{vmatrix}1 & 2 & 3& 4 \\5 & 6 &7 & 8 \\1 & 2 & 3 & 4\\13 & 14 & 15&16\end{vmatrix} D′=∣∣∣∣∣∣∣∣15113262143731548416∣∣∣∣∣∣∣∣。由于第一行和第三行是相等的,所以 D ′ = D D’=D D′=D;又由性质2,可以知道于 D ′ = − D D’=-D D′=−D。于是可知 D = D ′ = 0 D=D’=0 D=D′=0。
- 性质3:行列式的某一行都乘以k,等于用k乘以此行列式。
例如: 行列式 D = ∣ 1 2 3 4 k 5 k 6 k 7 8 9 ∣ = k ∣ 1 2 3 4 5 6 7 8 9 ∣ D=\begin{vmatrix}1 & 2 & 3 \\4k & 5k &6k \\7 & 8 & 9\end{vmatrix}=k\begin{vmatrix}1 & 2 & 3 \\4 & 5 &6 \\7 & 8 & 9\end{vmatrix} D=∣∣∣∣∣∣14k725k836k9∣∣∣∣∣∣=k∣∣∣∣∣∣147258369∣∣∣∣∣∣。
推论1: 行列式的某一行都有公因子 k k k,可以把 k k k提到外面。
推论2: 行列式的所有元素都有公因子 k k k, k k k朝外面提 n n n(对 n n n阶行列式而言)次。
例如: 行列式 D = ∣ 1 k 2 k 3 k 4 k 5 k 6 k 7 k 8 k 9 k ∣ = k 3 ∣ 1 2 3 4 5 6 7 8 9 ∣ D=\begin{vmatrix}1k & 2k & 3k \\4k & 5k &6k \\7k & 8k & 9k\end{vmatrix}=k^{3}\begin{vmatrix}1 & 2 & 3 \\4 & 5 &6 \\7 & 8 & 9\end{vmatrix} D=∣∣∣∣∣∣1k4k7k2k5k8k3k6k9k∣∣∣∣∣∣=k3∣∣∣∣∣∣147258369∣∣∣∣∣∣。
- 性质4:行列式的两行元素对应成比例,则行列式的值为零。
例如: 行列式 D = ∣ 1 2 3 4 5 6 8 10 12 ∣ = 2 ∣ 1 2 3 4 5 6 4 5 6 ∣ D=\begin{vmatrix}1 & 2 & 3 \\4 & 5 &6 \\8 & 10 &12\end{vmatrix}=2\begin{vmatrix}1 & 2 & 3 \\4 & 5 &6 \\4 & 5 &6\end{vmatrix} D=∣∣∣∣∣∣14825103612∣∣∣∣∣∣=2∣∣∣∣∣∣144255366∣∣∣∣∣∣,由性质2的推论,我们可以得出该行列式的值为0。
推论: 行列式的某一行全为0,则行列式的值为零。
针对上述的几种,行列式值为零的情况做一个总结:
- 性质5:行列式的某一行都为两项之和,可以拆分为两行项之和(和的那一行分开,其余行保持不变)。
例如: D = ∣ 1 2 3 4 + 1 5 + 2 6 + 3 7 8 9 ∣ = ∣ 1 2 3 4 5 6 4 5 6 ∣ + ∣ 1 2 3 1 2 3 4 5 6 ∣ D=\begin{vmatrix}1 & 2 & 3 \\4+1 & 5+2 &6 +3 \\7 & 8 &9\end{vmatrix}=\begin{vmatrix}1 & 2 & 3 \\4 & 5 &6 \\4 & 5 &6\end{vmatrix}+\begin{vmatrix}1 & 2 & 3 \\1 & 2 & 3 \\4 & 5 &6\end{vmatrix} D=∣∣∣∣∣∣14+1725+2836+39∣∣∣∣∣∣=∣∣∣∣∣∣144255366∣∣∣∣∣∣+∣∣∣∣∣∣114225336∣∣∣∣∣∣
小练习
D = ∣ b + c c + a a + b a + b b + c c + a c + a a + b b + c ∣ = ∣ b c a a + b b + c c + a c + a a + b b + c ∣ + ∣ c a b a + b b + c c + a c + a a + b b + c ∣ = ∣ b c a a b c c + a a + b b + c ∣ + ∣ b c a b c a c + a a + b b + c ∣ ∣ c a b a b c c + a a + b b + c ∣ + ∣ c a b b c a c + a a + b b + c ∣ = ∣ b c a a b c c a b ∣ + ∣ b c a a b c a b c ∣ + ∣ b c a b c a c a b ∣ + ∣ b c a b c a a b c ∣ + ∣ c a b a b c c a b ∣ + ∣ c a b a b c a b c ∣ + ∣ c a b b c a c a b ∣ + ∣ c a b b c a a b c ∣ \begin{aligned}D=&\begin{vmatrix}b+c & c+a & a+b \\a+b & b+c &c+a \\c+a & a+b &b+c\end{vmatrix}\\\\=&\begin{vmatrix}b & c & a \\a+b & b+c &c+a\\c+a & a+b &b+c\end{vmatrix}+\begin{vmatrix}c & a & b \\a+b & b+c &c+a\\c+a & a+b &b+c\end{vmatrix}\\\\=&\begin{vmatrix}b & c & a \\a & b&c\\c+a & a+b &b+c\end{vmatrix}+\begin{vmatrix}b & c & a \\b & c &a\\c+a & a+b &b+c\end{vmatrix}\begin{vmatrix}c & a & b \\a & b &c\\c+a & a+b &b+c\end{vmatrix}+\begin{vmatrix}c & a & b \\b & c &a\\c+a & a+b &b+c\end{vmatrix}\\\\=&\begin{vmatrix}b & c & a \\a & b&c\\c & a &b\end{vmatrix}+\begin{vmatrix}b & c & a \\a & b&c\\a & b &c\end{vmatrix}+\begin{vmatrix}b & c & a \\b & c &a\\c & a &b\end{vmatrix}+\begin{vmatrix}b & c & a \\b & c &a\\a & b &c\end{vmatrix}+\begin{vmatrix}c & a & b \\a & b &c\\c & a &b\end{vmatrix}+\begin{vmatrix}c & a & b \\a & b &c\\a & b &c\end{vmatrix}+\begin{vmatrix}c & a & b \\b & c &a\\c & a &b\end{vmatrix}+\begin{vmatrix}c & a & b \\b & c &a\\a & b &c\end{vmatrix}\end{aligned} D====∣∣∣∣∣∣b+ca+bc+ac+ab+ca+ba+bc+ab+c∣∣∣∣∣∣∣∣∣∣∣∣ba+bc+acb+ca+bac+ab+c∣∣∣∣∣∣+∣∣∣∣∣∣ca+bc+aab+ca+bbc+ab+c∣∣∣∣∣∣∣∣∣∣∣∣bac+acba+bacb+c∣∣∣∣∣∣+∣∣∣∣∣∣bbc+acca+baab+c∣∣∣∣∣∣∣∣∣∣∣∣cac+aaba+bbcb+c∣∣∣∣∣∣+∣∣∣∣∣∣cbc+aaca+bbab+c∣∣∣∣∣∣∣∣∣∣∣∣baccbaacb∣∣∣∣∣∣+∣∣∣∣∣∣baacbbacc∣∣∣∣∣∣+∣∣∣∣∣∣bbcccaaab∣∣∣∣∣∣+∣∣∣∣∣∣bbaccbaac∣∣∣∣∣∣+∣∣∣∣∣∣cacababcb∣∣∣∣∣∣+∣∣∣∣∣∣caaabbbcc∣∣∣∣∣∣+∣∣∣∣∣∣cbcacabab∣∣∣∣∣∣+∣∣∣∣∣∣cbaacbbac∣∣∣∣∣∣
- 性质6:行列式某一行乘以一个数,加到另一行上去,行列式的值不变。
例如: 把行列式 D = ∣ 1 2 3 4 5 6 7 8 9 ∣ D=\begin{vmatrix}1 & 2 & 3 \\4 & 5 &6 \\7 & 8 &9\end{vmatrix} D=∣∣∣∣∣∣147258369∣∣∣∣∣∣的第一行乘2,加到第二行去:
可以发现拆开的两项中,第二项里有两行对应成比例,所以第二项的值为0,因此,可以发现 D ′ = D D’=D D′=D,即得到性质6。
求解多阶行列式,通常是要把行列式化成上三角的形式。
参考文献
[1]宋浩.《线性代数》高清教学视频 “惊叹号”系列 宋浩老师[EB/OL].https://www.bilibili.com/video/BV1aW411Q7x1?p=3,2019-06-12.
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/37951.html