1. 编程号首页

CSAPP实验-CacheLab

编程小号 • • 未分类

CSAPP实验-CacheLabcachelab是csapp的配套实验之一，该实验分为A、B两个部分，A部分要求实现一个cache模拟器，B部分是实现一个针对cache优化的矩阵转置函数PartAPartA部分我们需要完成csim.c源文件，参考csim-ref程序接收相同的命令行参数并产生相同的输出。csim-ref是一个参考可执行程序，它能够模拟cache并处理valgrind生成的trace文件，它遵循LRU(最近使用)替换策略。我们的main函数要依次做如下几件事情：使用getopt库处理参数，保存cache的几个基本

cachelab是csapp的配套实验之一，该实验分为A、B两个部分，A部分要求实现一个cache模拟器，B部分是实现一个针对cache优化的矩阵转置函数

Part A

Part A部分我们需要完成csim.c源文件，参考csim-ref程序接收相同的命令行参数并产生相同的输出。csim-ref是一个参考可执行程序，它能够模拟cache并处理valgrind生成的trace文件，它遵循LRU(最近使用)替换策略。我们的main函数要依次做如下几件事情：

  • 使用getopt库处理参数，保存cache的几个基本参数如s、E、b，并根据基本参数计算其它参数如S、B、t等。
  • 根据这些参数初始化cache，这步需要使用malloc动态申请内存。
  • 读取trace文件并逐行处理每一个operation，其中I操作可以忽略，L和S操作访问cache一次，M操作访问cache两次，这是最关键的一步。
  • 关闭文件流并释放cache的内存。
  • 使用printSummary函数输出结果。

代码如下，关键部分已有注释：

#include <stdlib.h>
#include <stdio.h>
#include <getopt.h>
#include <stdbool.h>
#include <string.h>
#include "cachelab.h"

#define m (sizeof(void*)*8)

//块结构(不带数据)
struct block{ 
   
    bool valid;
    int tag;
    int timestamp;
};

int hits = 0;
int misses = 0;
int evictions = 0;

int timestamp = 0; //时间戳，每读取一个操作+1
bool verbose = false;
int s, E, b;
int S, B, t;
int C;
FILE *fp;
struct block ***cache;
char operationStr[256];

void printHelp(){ 
   
    printf("Help...\n");
}

//解析参数
void getOptions(int argc, char* argv[]){ 
   
    int opt;
    while((opt=getopt(argc, argv, "hvs:E:b:t:"))!=-1){ 
   
        switch (opt)
        { 
   
        case 'h':
            printHelp();
            exit(0);
        case 'v':
            verbose = true;
            break;
        case 's':
            s = atoi(optarg);
            S = 1<<s;
            break;
        case 'E':
            E = atoi(optarg);
            break;
        case 'b':
            b = atoi(optarg);
            B = 1<<b;
            break;
        case 't':
            fp = fopen(optarg, "r");
            if(fp == NULL){ 
   
                fprintf(stderr, "Open file failed");
                exit(-1);
            }
            break;
        default:
            break;
        }
    }
    t = m - (s+b);
    C = B*E*S;
}

//根据参数初始化cache
void initCache(){ 
   
    cache = malloc(sizeof(void*)*S);
    for(int i = 0; i<S; i++){ 
   
        cache[i] = malloc(sizeof(void*)*E);
        for(int j = 0; j<E; j++){ 
   
            struct block *pBlock = malloc(sizeof(struct block));
            pBlock->valid = false;
            pBlock->tag = 0;
            pBlock->timestamp = 0;
            cache[i][j] = pBlock;
        }
    }
}

//释放cache
void freeCache(){ 
   
    for(int i = 0; i<S; i++){ 
   
        for(int j = 0; j<E; j++){ 
   
            free(cache[i][j]);
        }
        free(cache[i]);
    }
    free(cache);
}

void callCache(unsigned long long address){ 
   
    int setAddress = address<<t>>(t+b);
    int tagAddress = address>>(s+b);
    struct block **pSet = cache[setAddress];
    struct block *pHitBlock = NULL;//命中的Block
    struct block *pEmptyBlock = NULL;//set中首个空的block
    struct block *pLRUBlock = NULL;//LRU策略下准备替换的block
    for(int i = 0; i<E; i++){ 
   
        struct block *pBlock = pSet[i];
        //找到对应tag的block即为命中缓存
        if(pHitBlock == NULL && pBlock->valid && pBlock->tag == tagAddress){ 
   
            pHitBlock = pBlock;
        }
        //遍历到的第一个空的block作为miss后使用的block
        if(pEmptyBlock == NULL && !pBlock->valid){ 
   
            pEmptyBlock = pBlock;
        }
        //timestamp最小的block即为最长时间没有访问的block
        if(pBlock->valid && (pLRUBlock == NULL || pLRUBlock->timestamp > pBlock->timestamp)){ 
   
            pLRUBlock = pBlock;
        }
    }

    if(pHitBlock!=NULL){ 
   
        hits++;
        if(verbose){ 
   
            printf(" hit");
        }
        pHitBlock->timestamp = timestamp;
    }
    else{ 
   
        misses++;
        if(verbose){ 
   
            printf(" miss");
        }
        if(pEmptyBlock!=NULL){ 
   
            pEmptyBlock->valid = true;
            pEmptyBlock->tag = tagAddress;
            pEmptyBlock->timestamp = timestamp;
        }
        else{ 
   
            //此时pLRUBlock必不为空
            if(pLRUBlock == NULL){ 
   
                printf("LRU Error\n");
                exit(-1);
            }
            evictions++;
            if(verbose){ 
   
                printf(" eviction");
            }
            pLRUBlock->tag = tagAddress;
            pLRUBlock->timestamp = timestamp;
        }
    }
}

//处理操作
void handleOpertaion(){ 
   
    timestamp++;
    char opType;
    unsigned long long address;
    int size;
    int count = sscanf(operationStr, " %c %llx,%d", &opType, &address, &size);

    //不匹配的行是I操作，忽略即可
    if(count==0){ 
   
        return;
    }
    if(verbose){ 
   
        printf("%s", operationStr);
    }
    switch (opType)
    { 
   
    case 'L':
        callCache(address);
        break;
    case 'S':
        callCache(address);
        break;
    case 'M': //M需要访问两次
        callCache(address);
        callCache(address);
        break;
    default:
        break;
    }
    if(verbose){ 
   
        printf("\n");
    }
}

void handleInput(){ 
   
    while(fgets(operationStr, 256, fp)){ 
   
        if(operationStr[strlen(operationStr)-1]=='\n'){ 
   
            operationStr[strlen(operationStr)-1]='\0';
        }
        handleOpertaion();
    }
}

int main(int argc, char* argv[])
{ 
   
    getOptions(argc, argv);
    initCache();
    handleInput();
    fclose(fp);
    freeCache();
    printSummary(hits, misses, evictions);
    return 0;
}

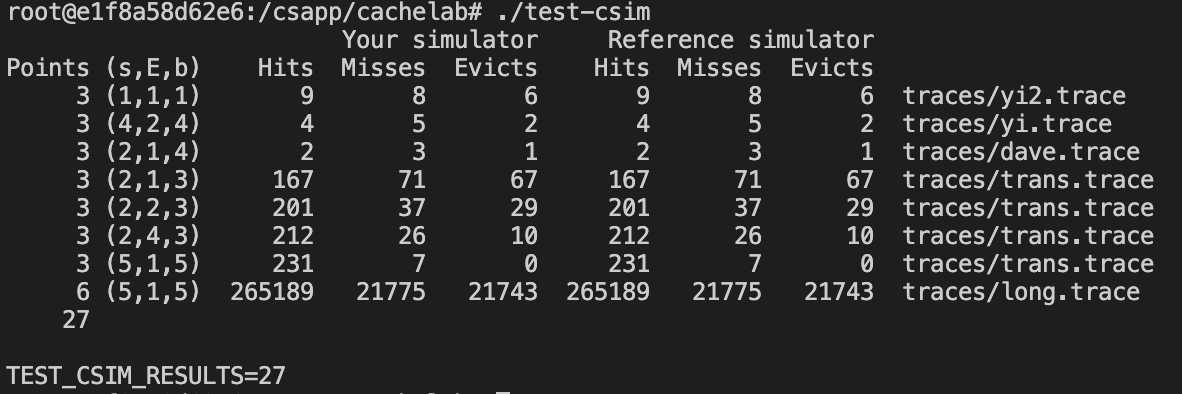
根据ReadMe中的指示，Make命令编译后，再运行测试程序test-csim，运行结果如下：
运行结果
得到27分即完成Part A。

Part B

Part B部分我们需要完成trans.c源文件，实现矩阵的转置同时要尽可能的减少cache miss。
首先如下指令安装valgrind

sudo apt install valgrind

注意在进行后续步骤前，要将当前实验目录移动到linux其它目录而非docker的共享文件夹中，否则会出现Program timed out，并且运行driver.py脚本需要python2.7环境。所谓cache friendly如何做到呢，现在脑子里有几个概念：

  • 程序要有良好的空间局部性和时间局部性。时间局部性是多次访问同一个地址尽可能在同一小时间段内(后面访问时该地址大概率在cache里)；空间局部性是在一小段时间内访问的地址尽可能靠近(这样两个地址更可能在同一个block内)。大部分业务层的代码做到这两点基本就够了
  • 对于性能要求苛刻的场景(大循环和重计算)，核心开销代码不得不考虑进行更深层次的cache优化。每个函数都可以视为自身 独占 完整的cache资源(就算刚执行时cache中都是其它数据，在函数执行一定时间后cache的大量block也会被替换为该函数访问的地址)，此时考虑cache的平均hit率，一个有效的策略是对于循环访问的数组进行分块。
32×32

首先计算cache的大小，在test-trans.c中使用的cache是(s=5,E=1,b=5)规格，每个block 2^5=32个字节，能存储8个int值；每一组只有一个块，一共有2^5=32组，所以cache能同时保存32*8=256个int值，也就是可以同时缓存256*4=1024字节=1M连续地址空间的内容。
分析给出的示例代码，单次循环要分别访问A[i][j]和B[j][i]一次，cache在执行该函数时被A和B数组共用。函数对A数组的是沿行遍历访问，效率尚可，对A的访问一共会产生32*4=128次左右miss。但是由于需要对数组转置，对B数组的遍历访问是沿列遍历访问，空间局部性很差，几乎每次访问都是miss，一共会产生1024次左右miss。我们的目标就清晰了，改进遍历方式，优化B数组访问的空间局部性，同时不对A的空间局部性产生影响。根据ppt的提示，我们可以使用分块的方式，也就是将A、B数组分成数个大小一致的正方块，只要保证访问每个块的空间局部性是较优的，那么让数组按块遍历的空间局部性也是较优的。由于cache至多可以存放32×32数组中连续8行的地址空间，所以我们选用8x8作为遍历的基本单位，A、B数组分别被分为16个块，平均每个块产生8次miss，理论上一共产生16*8*2=256次miss。

void transpose_submit(int M, int N, int A[N][M], int B[M][N])
{ 
   
    if(M == 32){ 
   
        int i, j, tmp;
        int k1, k2;
        for(k1 = 0; k1<32; k1+=8){ 
   
            for(k2=0; k2<32; k2+=8){ 
   
                for(i=0; i<8; i++){ 
   
                    for(j=0; j<8; j++){ 
   
                        tmp = A[k1+i][k2+j];
                        B[k2+j][k1+i] = tmp;
                    }
                }
            }
        }
    }
}

使用如上代码测试转置32×32的矩阵一共产生了343次miss，原因是A、B数组共用一个cache，所以某些块会出现A某行(对应B某列)使用cache的同一个block的情况，此时A、B不再能视为各自独立访问。简化计算可以假设A[0][0]和B[0][0]都使用cache的第0组，位于左对角线上的元素会额外产生一次miss，位于对角线上的块会多产生8次miss，每个数组的访问会多产生32次miss，这样理论上一共产生(16*8+32)*2=320次miss。此时就要考虑 时间局部性 的优化，由于题目限制不能在栈上定义超过12个局部变量，我们可以定义8个中间值tmp0～tmp7，将A数组块中一行的数据一次性取出分别赋给8个局部变量，然后在逐个赋给B数组块中一列的数据，这样对角线上的元素仅在访问B时才会产生一次额外miss，理论上一共产生16*8*2+32=288次。

void transpose_submit(int M, int N, int A[N][M], int B[M][N])
{ 
   
    if(M == 32){ 
   
        int i, tmp0,tmp1,tmp2,tmp3,tmp4,tmp5,tmp6,tmp7;
        int k1, k2;
        for(k1 = 0; k1<M; k1+=8){ 
   
            for(k2=0; k2<M; k2+=8){ 
   
                for(i=0; i<8; i++){ 
   
                    tmp0 = A[k1+i][k2];
                    tmp1 = A[k1+i][k2+1];
                    tmp2 = A[k1+i][k2+2];
                    tmp3 = A[k1+i][k2+3];
                    tmp4 = A[k1+i][k2+4];
                    tmp5 = A[k1+i][k2+5];
                    tmp6 = A[k1+i][k2+6];
                    tmp7 = A[k1+i][k2+7];
                    B[k2][k1+i] = tmp0;
                    B[k2+1][k1+i] = tmp1;
                    B[k2+2][k1+i] = tmp2;
                    B[k2+3][k1+i] = tmp3;
                    B[k2+4][k1+i] = tmp4;
                    B[k2+5][k1+i] = tmp5;
                    B[k2+6][k1+i] = tmp6;
                    B[k2+7][k1+i] = tmp7;
                }
            }
        }
    }
}

使用如上代码测试转置32×32的矩阵一共产生了287次miss符合预期，低于300次即可拿到满分。

64×64

对于64×64的矩阵，明显不能单纯使用8×8的分块策略，因为每行从32个值增加为64个值，此时cache至多可以存放64×64数组中连续4行的地址空间。按照之前的思路我们选用 4x4的分块策略，数组将被分为256个块，那么理论上共会产生256*4*256*2+64=1600次miss,实际测试时发现产生了1699次miss，没达到满分1300次以内的要求，只得到了3.4分，原因是在4×4分块时cache的利用率较低。看了下网上的解决方案都比较复杂，这种针对特定场景的高级别的优化基本可以看作是纯粹的脑力训练，这里我就不求甚解了，代码如下

void transpose_submit(int M, int N, int A[N][M], int B[M][N]){ 
   
    if(M == 64){ 
   
        int i, tmp0,tmp1,tmp2,tmp3;
        int k1, k2;
        for(k1 = 0; k1<M; k1+=4){ 
   
            for(k2=0; k2<N; k2+=4){ 
   
                for(i=0;i<4;i++){ 
   
                    tmp0 = A[k1+i][k2];
                    tmp1 = A[k1+i][k2+1];
                    tmp2 = A[k1+i][k2+2];
                    tmp3 = A[k1+i][k2+3];
                    B[k2][k1+i] = tmp0;
                    B[k2+1][k1+i] = tmp1;
                    B[k2+2][k1+i] = tmp2;
                    B[k2+3][k1+i] = tmp3;
                }
            }
        }
    }
}
61×67

对于不规则61×67的矩阵，可以先对60×60的矩阵使用4×4的分块策略，剩下的部分直接用最原始的赋值即可。代码如下：

void transpose_submit(int M, int N, int A[N][M], int B[M][N]){ 
   
    if(M == 61){ 
   
        int i, tmp0,tmp1,tmp2,tmp3;
        int k1, k2;
        int k1_max = M/4*4;
        int k2_max = N/4*4;
        for(k1 = 0; k1<k1_max; k1+=4){ 
   
            for(k2=0; k2<k2_max; k2+=4){ 
   
                for(i=0;i<4;i++){ 
   
                    tmp0 = A[k1+i][k2];
                    tmp1 = A[k1+i][k2+1];
                    tmp2 = A[k1+i][k2+2];
                    tmp3 = A[k1+i][k2+3];
                    B[k2][k1+i] = tmp0;
                    B[k2+1][k1+i] = tmp1;
                    B[k2+2][k1+i] = tmp2;
                    B[k2+3][k1+i] = tmp3;
                }
            }
        }
        for(k1=k1_max; k1<M; k1++){ 
   
            for(k2=0; k2<k2_max; k2++){ 
   
                tmp0 = A[k1][k2];
                B[k2][k1] = tmp0;
            }
        }
        for(k1=0; k1<k1_max; k1++){ 
   
            for(k2=k2_max; k2<N; k2++){ 
   
                tmp0 = A[k1][k2];
                B[k2][k1] = tmp0;
            }
        }
        for(k1=k1_max; k1<M; k1++){ 
   
            for(k2=k2_max; k2<N; k2++){ 
   
                tmp0 = A[k1][k2];
                B[k2][k1] = tmp0;
            }
        }
    }
}

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请发送邮件至 举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/38135.html

赞 (0)
编程小号编程小号
0

相关推荐

发表回复

您的电子邮箱地址不会被公开。 必填项已用*标注