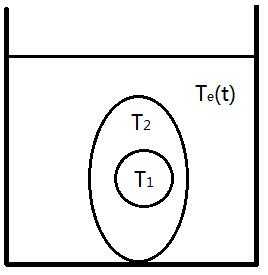
一,上一讲的例题,如图:
设 x = T 1 x=T_1 x=T1, y = T 2 y=T_2 y=T2
方程组为·: { x ′ = − 2 x + 2 y y ′ = 2 x − 5 y \left\{\begin{matrix}{x}'=-2x+2y\\ {y}'=2x-5y\end{matrix}\right. {
x′=−2x+2yy′=2x−5y
用消元法求出的通解为: { x = c 1 e − t + c 2 e − 6 t y = 1 2 c 1 e − t − 2 c 2 e − 6 t \left\{\begin{matrix}x=c_{1}e^{-t}+c_{2}e^{-6t}\\ y=\frac{1}{2}c_{1}e^{-t}-2c_{2}e^{-6t}\end{matrix}\right. {
x=c1e−t+c2e−6ty=21c1e−t−2c2e−6t
二,用矩阵重新表示方程组:
[ x ′ y ′ ] = [ − 2 2 2 − 5 ] [ x y ] \begin{bmatrix}{x}'\\ {y}'\end{bmatrix}=\begin{bmatrix} -2 &2 \\ 2 & -5\end{bmatrix}\begin{bmatrix}x\\ y\end{bmatrix} [x′y′]=[−222−5][xy]
三,用矩阵重新表示通解:
[ x y ] = c 1 [ 1 1 2 ] e − t + c 2 [ 1 − 2 ] e − 6 t \begin{bmatrix}x\\ y\end{bmatrix}=c_{1}\begin{bmatrix} 1\\ \frac{1}{2}\end{bmatrix}e^{-t}+c_{2}\begin{bmatrix}1\\ -2\end{bmatrix}e^{-6t} [xy]=c1[121]e−t+c2[1−2]e−6t
四,设解的形式为:
[ x y ] = [ a 1 a 2 ] e λ t \begin{bmatrix}x\\ y\end{bmatrix}=\begin{bmatrix} a_{1}\\ a_{2}\end{bmatrix}e^{\lambda t} [xy]=[a1a2]eλt
五,将解带入方程组:
[ x ′ y ′ ] = λ [ a 1 a 2 ] e λ t = [ − 2 2 2 − 5 ] [ a 1 a 2 ] e λ t = [ − 2 2 2 − 5 ] [ x y ] \begin{bmatrix}{x}'\\ {y}'\end{bmatrix}=\lambda \begin{bmatrix} a_{1}\\ a_{2}\end{bmatrix}e^{\lambda t}=\begin{bmatrix} -2 &2 \\ 2 & -5\end{bmatrix}\begin{bmatrix}a_{1}\\ a_{2} \end{bmatrix}e^{\lambda t}=\begin{bmatrix} -2 &2 \\ 2 & -5\end{bmatrix}\begin{bmatrix}x\\ y\end{bmatrix} [x′y′]=λ[a1a2]eλt=[−222−5][a1a2]eλt=[−222−5][xy]
六,化简,求出特征值:
- λ [ a 1 a 2 ] = [ − 2 2 2 − 5 ] [ a 1 a 2 ] \lambda \begin{bmatrix} a_{1}\\ a_{2}\end{bmatrix}=\begin{bmatrix} -2 &2 \\ 2 & -5\end{bmatrix}\begin{bmatrix}a_{1}\\ a_{2} \end{bmatrix} λ[a1a2]=[−222−5][a1a2]
- [ − 2 2 2 − 5 ] [ a 1 a 2 ] − λ [ a 1 a 2 ] = 0 \begin{bmatrix}-2 &2 \\ 2 & -5\end{bmatrix}\begin{bmatrix}a_{1}\\ a_{2} \end{bmatrix}-\lambda \begin{bmatrix}a_{1}\\ a_{2}\end{bmatrix}=0 [−222−5][a1a2]−λ[a1a2]=0
- [ − 2 − λ 2 2 − 5 − λ ] [ a 1 a 2 ] = 0 \begin{bmatrix}-2-\lambda &2 \\ 2 & -5-\lambda \end{bmatrix}\begin{bmatrix}a_{1}\\ a_{2} \end{bmatrix}=0 [−2−λ22−5−λ][a1a2]=0
- 要使等式有非0解,必须满足: ∣ − 2 − λ 2 2 − 5 − λ ∣ = 0 \begin{vmatrix}-2-\lambda & 2 \\ 2 & -5-\lambda \end{vmatrix}=0 ∣∣∣∣−2−λ22−5−λ∣∣∣∣=0
- 解得: λ 1 = − 1 , λ 2 = − 6 \lambda _{1}=-1, \lambda _{2}=-6 λ1=−1,λ2=−6,(答案跟上一讲求的特征值一样)
七,将 λ 1 \lambda _{1} λ1和 λ 2 \lambda _{2} λ2分别代入等式,求出特征向量:
- 将 λ 1 \lambda _{1} λ1代入: [ − 1 2 2 − 4 ] [ a 1 a 2 ] = 0 \begin{bmatrix}-1 &2 \\ 2 & -4 \end{bmatrix}\begin{bmatrix}a_{1}\\ a_{2} \end{bmatrix}=0 [−122−4][a1a2]=0
- 设自由变量 a 1 = 1 a_{1}=1 a1=1,则 a 2 = 1 2 a_{2}=\frac{1}{2} a2=21, [ a 1 a 2 ] = c 1 [ 1 1 2 ] \begin{bmatrix}a_{1}\\ a_{2}\end{bmatrix}=c_{1}\begin{bmatrix}1 \\ \frac{1}{2}\end{bmatrix} [a1a2]=c1[121], c 1 c_{1} c1为任意常数
- [ x y ] = [ a 1 a 2 ] e λ t = c 1 [ 1 1 2 ] e − t \begin{bmatrix}x\\ y\end{bmatrix}=\begin{bmatrix}a_{1}\\ a_{2}\end{bmatrix}e^{\lambda t}=c_{1}\begin{bmatrix}1 \\ \frac{1}{2}\end{bmatrix}e^{-t} [xy]=[a1a2]eλt=c1[121]e−t
- 将 λ 2 \lambda _{2} λ2代入: [ 4 2 2 1 ] [ a 1 a 2 ] = 0 \begin{bmatrix}4 &2 \\ 2 & 1 \end{bmatrix}\begin{bmatrix}a_{1}\\ a_{2} \end{bmatrix}=0 [4221][a1a2]=0
- 设自由变量 a 1 = 1 a_{1}=1 a1=1,则 a 2 = − 2 a_{2}=-2 a2=−2, [ a 1 a 2 ] = c 2 [ 1 − 2 ] \begin{bmatrix}a_{1}\\ a_{2}\end{bmatrix}=c_{2}\begin{bmatrix}1 \\ -2\end{bmatrix} [a1a2]=c2[1−2], c 2 c_{2} c2为任意常数
- [ x y ] = [ a 1 a 2 ] e λ t = c 2 [ 1 − 2 ] e − 6 t \begin{bmatrix}x\\ y\end{bmatrix}=\begin{bmatrix}a_{1}\\ a_{2}\end{bmatrix}e^{\lambda t}=c_{2}\begin{bmatrix}1 \\ -2\end{bmatrix}e^{-6t} [xy]=[a1a2]eλt=c2[1−2]e−6t
八,得解空间:
[ x y ] = c 1 [ 1 1 2 ] e − t + c 2 [ 1 − 2 ] e − 6 t \begin{bmatrix}x\\ y\end{bmatrix}=c_{1}\begin{bmatrix} 1\\ \frac{1}{2}\end{bmatrix}e^{-t}+c_{2}\begin{bmatrix}1\\ -2\end{bmatrix}e^{-6t} [xy]=c1[121]e−t+c2[1−2]e−6t
九,二阶矩阵的特征值是如下方程的解:
λ 2 − t r a c e ( A ) λ + d e t A = 0 \lambda ^{2}-trace(A)\lambda +detA =0 λ2−trace(A)λ+detA=0
trace(A)是A的迹,detA是A的行列式
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/38261.html