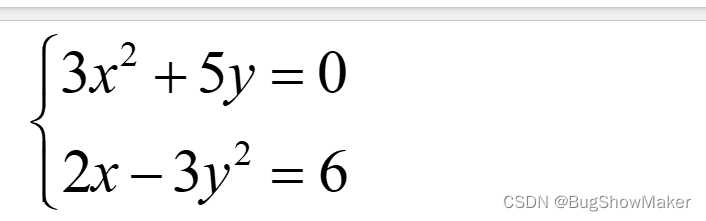方程解的分类

方程解有两类：

1.数值解 — 近似解

2.符号解 — 精确解

为什么会产生这两类？ 

求方程的符号解

将方程的解用符号表示而不是一个具体的数值，此时方程的解叫做方程的符号解

一元一次方程

slove(F,x) 以x为变量 F关系式的解

案例：

a*x^2+b*x+c = 0求解

syms a b c x;
f = a*x^2+b*x+c;
solve(f,x)

结果：

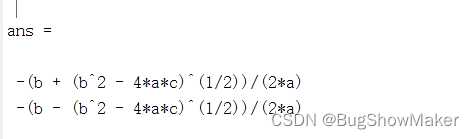
案例2：

syms a b c x;
f = x^3-2*x+1;
solve(f,x)

结果：

一元二次方程组

使用方法 [x,y] = solve(f1,f2,x,y)

案例：

syms x y;
f1 = 3*x^2+5*y;
f2 = 2*x-3*y-6;
[x,y] = solve(f1,f2,x,y)

结果：

 求方程的数值解

 当我们使用solve求不出一个一元函数具体的解（值<1）时。方法如下：

1.作图观察零点位置

使用相应的作图方法

2.利用近似解方法确定解

//两个零点的利用

 x = fzero (F,x0)

x = fzero(F,[x0,y0])

//方程近似解的求解

[x,f,h] = fsolve(f,x0) 当h趋近于0 表示结果可靠