学习目标:
(一)了解递归算法思想
(二)用递归思想来理解和实现递归经典实例
I.阶乘问题
II.斐波那契问题
III.汉诺塔问题
IV.全排列问题
 _全排列” style=”width: 520px; visibility: visible; height: 520px;”>
_全排列” style=”width: 520px; visibility: visible; height: 520px;”>
(一)递归
I. 定义
递归算法(英语:recursion algorithm)在计算机科学中是指一种通过重复将问题分解为同类的子问题而解决问题的方法。
需要满足的条件:
(1)子问题和原始问题要执行的操作应该是一致的,通常来说,子问题规模更小,更为简单。
(2)不能无限制的调用自身,需要有一个出口,化简为非递归的情况进行处理。
II.递归算法的特点
(1) 递归就是在过程或函数里调用自身。
(2) 在使用递归策略时,必须有一个明确的递归结束条件,称为递归出 口。
(3) 递归算法解题通常显得很简洁,但递归算法解题的运行效率较低。 所以一般不提倡用递归算法设计程序。
(4) 在递归调用的过程当中系统为每一层的返回点、局部量等开辟了栈 来存储。递归次数过多容易造成栈溢出等。
III.执行过程
(1)向下递推:通过多次调用自身函数进行下递推,直到满足终止条件
(2)向上回归:达到终止条件后,返回执行,直到得到最终结果
IV.递归要素
(1)递归方程
(2)边界条件
(二)经典递归算法应用实例
I.阶乘问题
给出任意一个正整数n,求解其阶层?

解决问题方式:
//阶层函数
int Fact(int n){
if(n==0)return 1;
else return n*Fact(n-1);
}
int main(){
int n,total;
printf("请输入正整数n:\n");
scanf("%d",&n);
total=Fact(n);
printf("%d的阶层为:%d\n",n,total);
return 0;
}
运行结果演示:

弊端:如果正整数过大,其就无法算出结果
利用斯特林公式来求大数阶乘
公式一:

公式二:

代码实现如下:
using namespace std;
//结点
struct bigNum
{
double n; //科学计数法表示的尾数部分
int e; //科学计数法表示的指数部分,若一个bigNum为x,这x=n * 10^e
};
//const修饰的量为一个常变量,需要初始化
const double a1[]=
{ 1.00, 1.0/12.0, 1.0/288, -139/51840,-571.0/2488320.0 };//
const double a2[]=
{ 1.0/12.0, -1.0/360, 1.0/1260.0 };
void printfResult(struct bigNum *p,char buff[])
{
while (p->n >=10.00 )
{p->n/=10.00; p->e++;}
sprintf(buff,"%.14fe%d",p->n,p->e);
}
// n!=sqrt(2*PI*n)*(n/e)^n*(1+ 1/12/n+ 1/288/n^2 -139/51840/n^3-571/2488320/n^4+…)
void calcFac1(struct bigNum *p,int n)
{
double logx,
s, //级数的和
item; //级数的每一项
int i;
// x^n= pow(10,n * log10(x));
logx= n* log10((double)n/E);
p->e= (int)(logx);
p->n= pow(10.0, logx-p->e);
p->n *= sqrt( 2* PI* (double)n);
//求(1+ 1/12/n+ 1/288/n^2 -139/51840/n^3-571/2488320/n^4+…)
for (item=1.0,s=0.0,i=0;i<sizeof(a1)/sizeof(double);i++)
{
s=s + item * a1[i];//求和
item= 1/(n^i);
}
p->n *=s;
}
//ln(n!)=0.5*ln(2*PI)+(n+0.5)*ln(n)-n+(1/12/n -1/360/n^3 + 1/1260/n^5 -...)
void calcFac2(struct bigNum *p,int n)
{
double logR;
double s, //级数的和
item; //级数的每一项
int i;
logR=0.5*log(2.0*PI)+((double)n+0.5)*log(n)-(double)n;
// s= (1/12/n -1/360/n^3 + 1/1260/n^5)
for (item=1/(double)n,s=0.0,i=0;i<sizeof(a2)/sizeof(double);i++)
{
s+= item * a2[i];
item /= (double)(n)* (double)n; //item= 1/(n^(2i+1))
}
logR+=s;
//根据换底公式,log10(n)=ln(n)/ln(10)
p->e = (int)( logR / log(10));
p->n = pow(10.00, logR/log(10) - p->e);
}
int main(int argc, char* argv[])
{
struct bigNum r;
char buff[32];
int n;
printf("请输入正整数n:\n");
scanf("%d",&n);
calcFac1(&r,n); //用第一种方法,计算n的阶乘
printfResult(&r,buff); //将结果转化一个字符串
printf("方法一:%d!=%s ",n,buff);
printf("\n");
calcFac2(&r,n); //用第二种方法,计算n的阶乘
printfResult(&r,buff); //将结果转化一个字符串
printf("方法二:%d!=%s ",n,buff);
return 0;
}
运行结果演示:

https://mathworld.wolfram.com/Series.html(公式来源)
II.斐波那契数列


斐波那契函数如下:

代码实现如下:
//斐波那契函数
int Fib(int n){
if(n==1||n==2)return 1; //递归终止条件
else return Fib(n-1)+Fib(n-2); //递归步骤
}
int main(){
int n,total;
printf("请输入几个月后:\n");
scanf("%d",&n);
total=Fib(n);
printf("%d月后的兔子总数为:%d\n",n,total);
return 0;
}
运行结果:

III.汉诺塔问题
相传在古印度圣庙中,有一种被称为汉诺塔(Hanoi)的游戏。该游戏是在一块铜板装置上,有三根杆(编号A、B、C),在A杆自下而上、由大到小按顺序放置64个金盘。

游戏的目标:把A杆上的金盘全部移到C杆上,并仍保持原有顺序叠好。
操作规则:每次只能移动一个盘子,并且在移动过程中三根杆上都始终保持大盘在下,小盘在上,操作过程中盘子可以置于A、B、C任一杆上。
问题分析:
(1)以C盘为中介,从A杆将1至n-1号盘移至B杆;
(2)将A杆中剩下的第n号盘移至C杆
(3)以A杆为中介;从B杆将1至n-1号盘移动至C杆
简单实例讲解(n=3)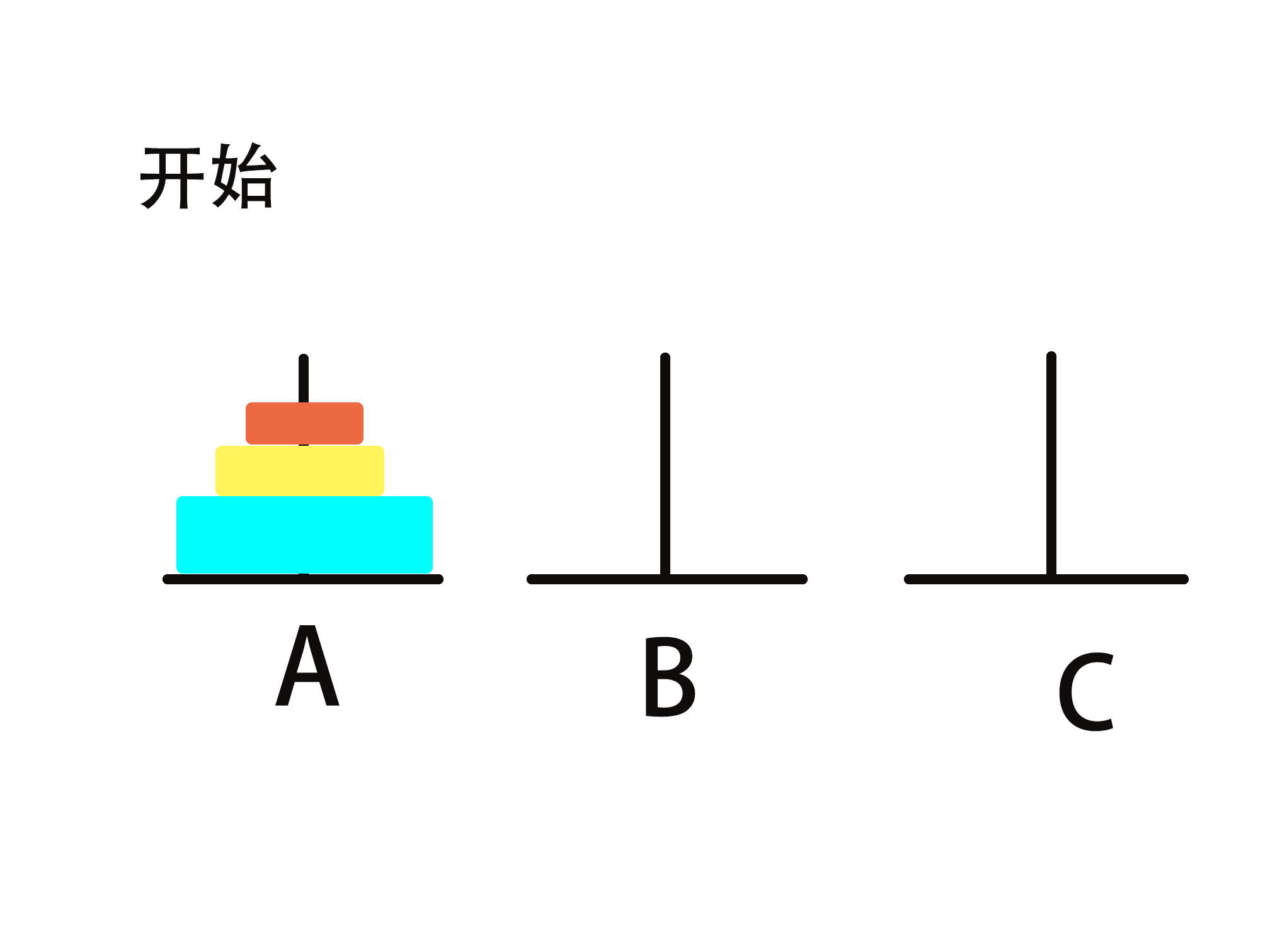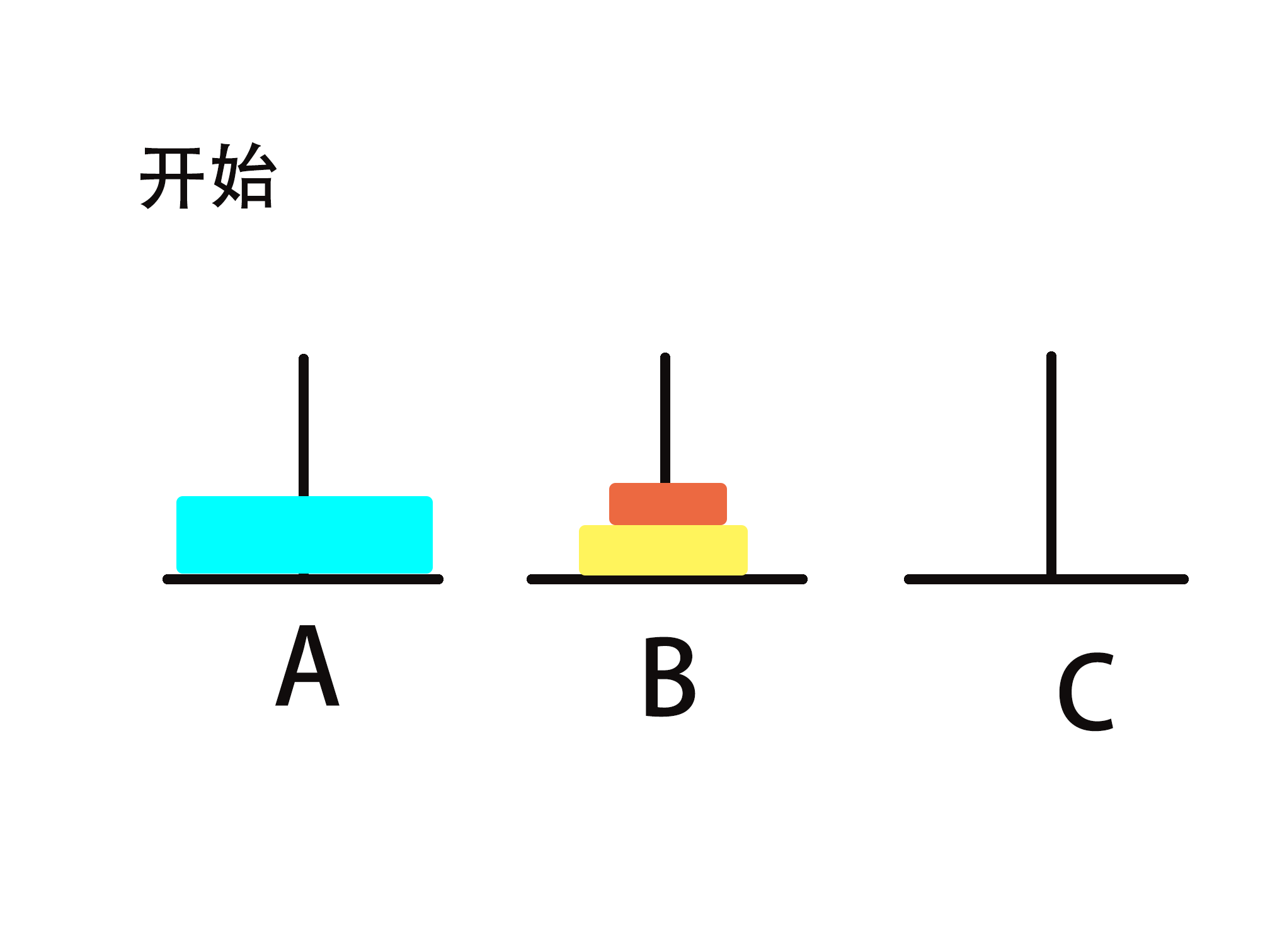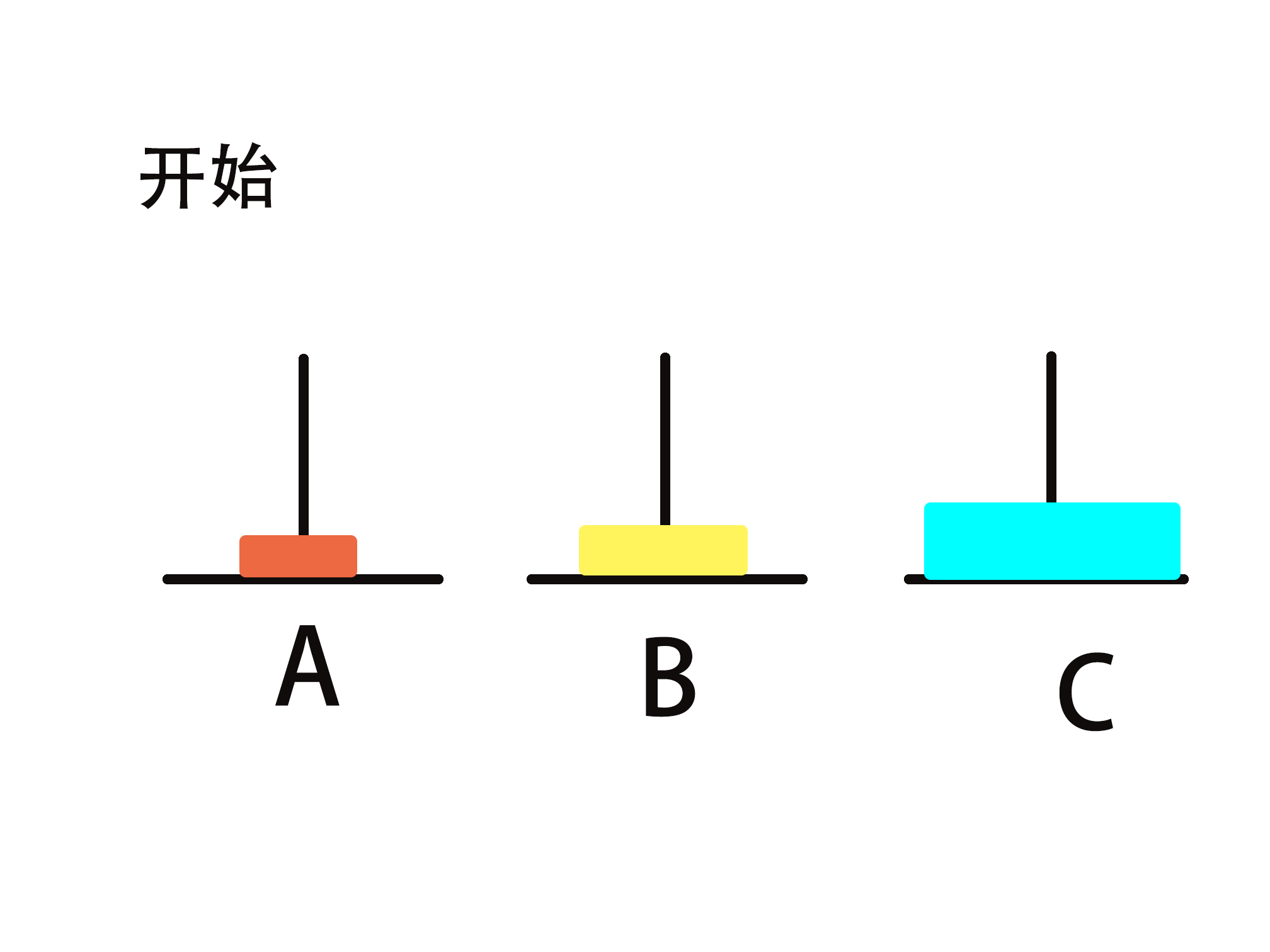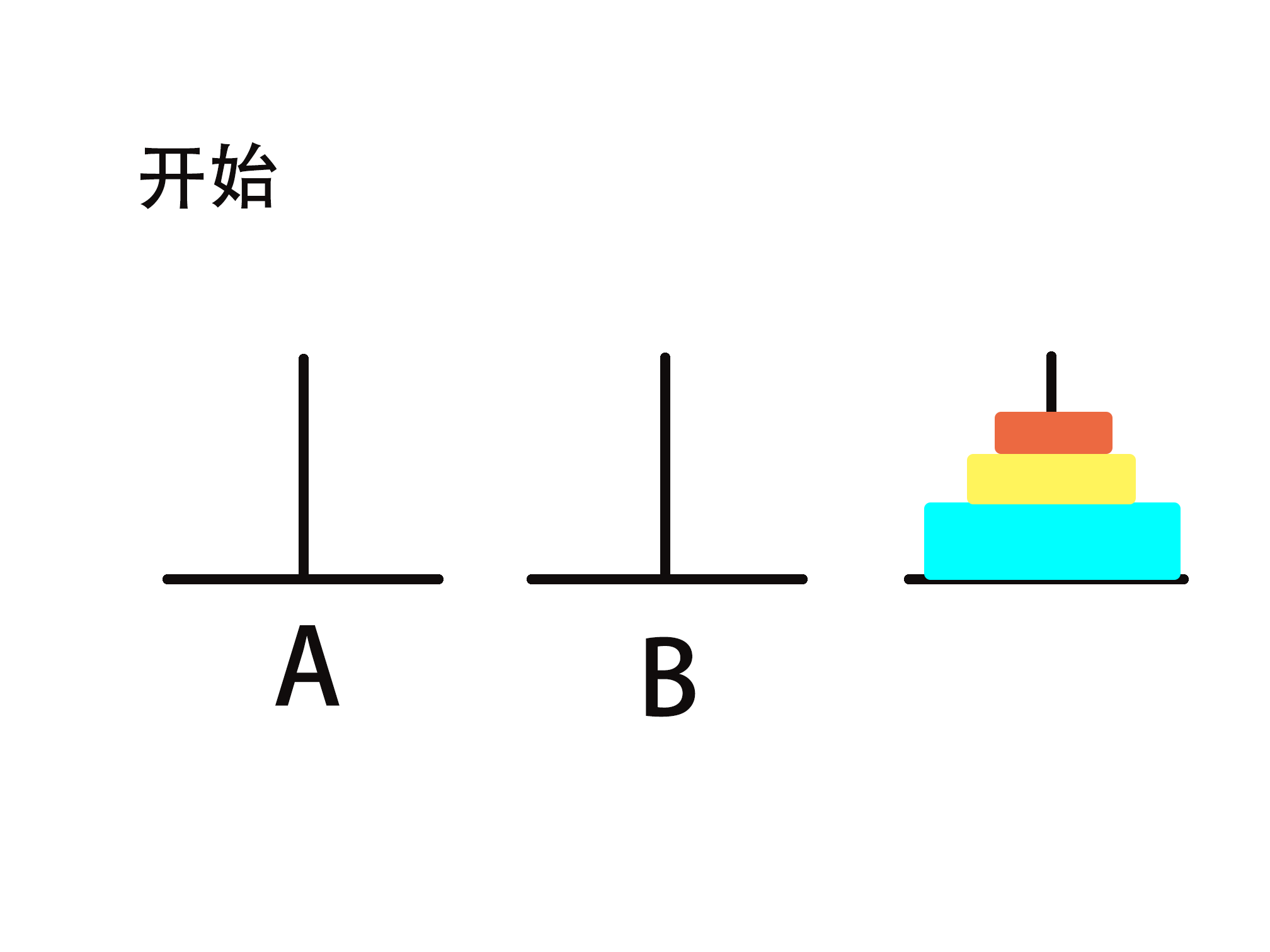
移动步骤(从上到下编号为1~3):
第一步:将 1 从 A->C
第二步:将 2 从 A->B
第三步:将 1 从 C->B
第四步:将 3 从 A->C
第五步:将 1 从 B->A
第六步:将 2 从 B->C
第七步:将 1 从 A->C
总结:先是以C杆为中间媒介,然后是以A杆为中间媒介
代码实现如下:
/*汉诺塔问题 规则:每次只能移动一个柱子 */
//函数声明
void move(char A,int n,int *m,char C); //输出移动路线
void Hanoi(int n,int *m,char A,char B,char C); //汉诺塔函数
//主函数
int main(){
int m=0; //记录搬动次数
int*q = &m;
int n;
char a='A';
char b='B';
char c='C';
printf("请输入汉诺塔层数:\n");
scanf("%d",&n);
Hanoi(n,q,a,b,c); //调用汉诺塔函数
printf("总移动次数为:%d\n",m);
return 0;
}
void move(char A,int n,int* m,char C)
{
printf("第 %d 次: 编号为%d 移动: %c -> %c\n",++(*m),n,A,C);
}
//汉诺塔函数
void Hanoi(int n,int *m,char A,char B,char C){
//将塔座A上的n个圆盘按规则搬到C上,B做辅助塔
if(n==1) move(A,1,m,C); //将编号为1的圆盘从A移动到C
else{
Hanoi(n-1,m,A,C,B); //将A上编号为1至n-1的圆盘移动到B,C做辅助塔
move(A,n,m,C); //将编号为n的圆盘从A移动到C
Hanoi(n-1,m,B,A,C); //将B上编号为1至n-1的圆盘移动到C,A做辅助塔
}
}
结果测试:


IV.全排列
问题引入:
从n个不同元素中任取m(m≤n)个元素,按照一定的顺序排列起来,叫做从n个不同元素中取出m个元素的一个排列。当m=n时所有的排列情况叫全排列

算法思想:
任取一个数作为第一个数,要求n-1个数的全排序,则要求n-2个数的全排序……直到要求的全排序只有一个数,找到出口。
/*递归实现全排列*/
//交换函数值
void swap(int arr[],int m,int n)
{
int temp=arr[m];
arr[m]=arr[n];
arr[n]=temp;
}
//全排列
void All_permutation(int arr[],int p,int q)
{
if(p==q) //递归出口
{
for( int i=0;i<=q;i++)
printf(" %d ",arr[i]);
putchar('\n');
}
else
{
for(int i=p;i<=q;i++) //将每个数据依次放在第一个位置
{
swap(arr,p,i);
All_permutation(arr,p+1,q); //剩下的n-1个数进行全排列
swap(arr,p,i); //将下一个数放在第一位之前应让之前调换的数据归位
}
}
}
int main()
{
int i;
int *arr;
int N;
printf("请输入你要全排列的数据个数:\n");
scanf("%d",&N);
for(i =0;i<N;i++)
arr[i]=i+1;
printf("全排列结果为:\n");
All_permutation(arr,0,N-1);
return 0;
}
结果测试:

版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/39569.html

 _全排列” style=”width: 520px; visibility: visible; height: 520px;”>
_全排列” style=”width: 520px; visibility: visible; height: 520px;”>