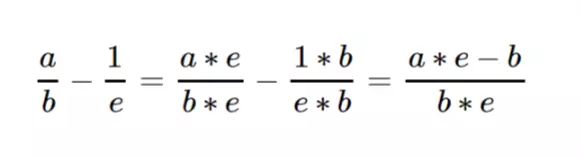南师大C：真分数分解为埃及分数

前言

通过这道题目稍许了解了贪心算法，不多说直接看下文吧

正文

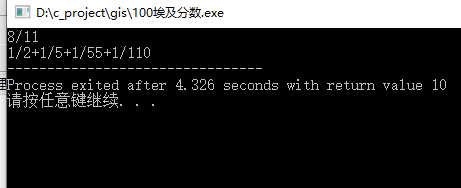
题目描述：分子为1的分数称为埃及分数。现输入一个真分数(分子比分母小的分数，叫做真分数)，请将该分数分解为埃及分数。
如：8/11 = 1/2+1/5+1/55+1/110。

关键

贪心算法（又称贪婪算法）是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所做出的是在某种意义上的局部最优解

由于贪心算法的每次都是贪婪选择的特性，我们可以用7/8来举例，小一点的埃及分数是怎么算出来的，你完全可以举例，前提是埃及分数必须要 1/x 的形式。

• 比7/8小一点的埃及分数 是多少，应该是 1/2 （ 4/8），去除1/2后剩3/8。
• 比3/8小一点的埃及分数是 1/3（3/9），去除之后剩 1/ 24 ，得到最终答案。
• 7/8 = 1/2 + 1/3 +1/24

如何得到最大埃及分数就是解题的关键，下面是的推导过程

推导过程

已经可以证明1/(c +1) 是 a/b的埃及分数了，但为什么说1/(c + 1)是a/b 所包含的
最大埃及分数？
其实可以由[4] 得出 a/b = 1 / (c + d/a) ，而d/a一定小于1，我们要找最大的埃及分数，就要取一个最小的整数分母，而最小（最接近）的整数分母就是 c + 1了，所以1/(c + 1)一定是其包含的最大的埃及分数了

下面我们设 e = c + 1(注意，1/e是最大埃及分数)
按照上面我们所说，一个真分数减去它的最大埃及分数。
运算出来就是：

我们就可以知道 一个真分数减去一个最大埃及分数之后
原来的a 变成了，a * e – b，原来的b变成了 b * e
感谢大佬的推导：https://www.jianshu.com/p/da04c77e11d0

代码

#include <stdio.h>
int main()
{ 
   
	int a,b;
	scanf("%d/%d",&a,&b);/*输入分子a和分母b*/
	int c;int d;
	while(1){ 
   
		c=b/a;
		d=c+1;//最大埃及分数1/c+1 
		if(b%a==0){ 
   /*若除得尽，输出最后一项*/
			printf("1/%d",b/a);
			break;
		}
		else{ 
   /*若分子不能整除分母，则分解出一个最大埃及分数1/c+1 */
			printf("1/%d+",d);
		}
		a=a*d-b;
		b=b*d;
		if(a==3&&b%2==0){ 
   /*若余数分子为3，分母为偶数，输出最后两个埃及分数*/
			printf("1/%d+1/%d",b/2,b);
			break;
		} 
	}
}

今天的文章南师大C：真分数分解为埃及分数分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。