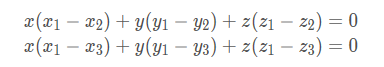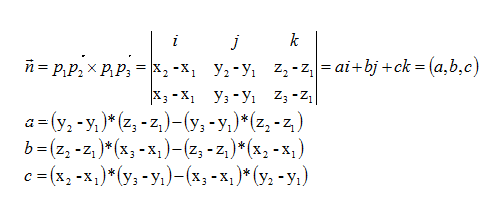编程这么久了还没有一个自己常用的数学库,每每需要求解什么算法,都在网上查找相关资料,不过好处是可以复习一些已经忘却很久的知识,体验一下温故而知新。
背景知识
向量积,已知向量
a=(a1,a2,a3) b=(b1,b2,b3)
其向量积可表示为:
a×b=(a2b3-a3b2,a3b1-a1b3,a1b2-a2b1)
问题抽象
已知三点 P1(x1,y1,y1),P2(x2,y2,y2),P3(x3,y3,y3)。要求求出这三个点构成平面的法向量。
高中知识解法
我们知道法向量是和平面垂直的,因此法向量也和该平面上任意一条向量垂直,即点乘积为 0。
利用这个性质,我们可以构造两个方程,此时我们不妨设法向量 n→=(x,y,z) 。
将 P1 P2 P3 坐标带入即可。
然后我们不妨假设 x=1, 这样即可求出 x y z(三个方程三个未知量)。
大学知识解法
具体代码
//计算三点成面的法向量 三个点v1,v2,v3,法向量vn void GetNormal(const Vec3d& v1, const Vec3d& v2, const Vec3d& v3, Vec3d &vn) { double na = (v2.y - v1.y)*(v3.z - v1.z) - (v2.z - v1.z)*(v3.y - v1.y); double nb = (v2.z - v1.z)*(v3.x - v1.x) - (v2.x - v1.x)*(v3.z - v1.z); double nc = (v2.x - v1.x)*(v3.y - v1.y) - (v2.y - v1.y)*(v3.x - v1.x); //平面法向量 vn.Set(na, nb, nc); }
转载于:https://www.cnblogs.com/ice-arrow/p/11120405.html
今天的文章按右手定则求已经知三点的法向量分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/4545.html