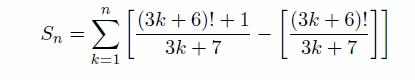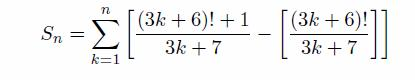威尔逊定理B

题目

The math department has been having problems lately. Due to immense amount of unsolicited automated programs which were crawling across their pages, they decided to put Yet-Another-Public-Turing-Test-to-Tell-Computers-and-Humans-Apart on their webpages. In short, to get access to their scientific papers, one have to prove yourself eligible and worthy, i.e. solve a mathematic riddle.

However, the test turned out difficult for some math PhD students and even for some professors. Therefore, the math department wants to write a helper program which solves this task (it is not irrational, as they are going to make money on selling the program).

The task that is presented to anyone visiting the start page of the math department is as follows: given a natural n, compute

where [x] denotes the largest integer not greater than x.

Input
The first line contains the number of queries t (t ≤ 10^6). Each query consist of one natural number n (1 ≤n ≤10^6).

Output
For each n given in the input output the value of Sn.

Sample Input
13
1
2
3
4
5
6
7
8
9
10
100
1000
10000

Sample Output
0
1
1
2
2
2
2
3
3
4
28
207
1609

题目翻译一下啦~
数学系最近遇到了问题。 由于大量未经请求的自动程序在他们的网页上爬行，他们决定在他们的网页上放置Yet-Another-Public-Turing-Test-to-Tell-Computers-and-Humans-Apart。 简而言之，要获得他们的科学论文，必须证明自己有资格和有价值，即解决数学之谜。

然而，对于一些数学博士生甚至一些教授来说，测试结果很难。 因此，数学系想要编写一个帮助程序来解决这个任务（这不是不合理的，因为他们会在出售程序时赚钱）。

呈现给访问数学部门起始页面的任何人的任务如下：给定一个自然的n，计算

其中[x]表示不大于x的最大整数。

输入
第一行包含查询数t（t ≤ 10 ^ 6）。 每个查询由一个自然数n组成（1 ≤ n ≤ 10 ^ 6）。

输出
对于输入输出中给出的每个n，Sn的值。

思路：既然说用到威尔逊定理，那么肯定是的啦，我们首先分析后面一个取整
(3x+6)! /(3x+7) 和威尔逊定理的很像，都少了一
如果3x+7为合数，由威尔逊定理知,此时3x+7>4，所以(3x+6)!/(3x+7) 可以整除，那么表示取整符号对这个没有影响，所以此时式子为 [1/3x+7]=0,此时结果为0
如果3x+7为素数，同理可知，此时(3x+6)!=(3x+6)(mod 3x+7),所以另(3x+6)!=k(3x+7)+3x+6,所以后面一个取整为k,前面式子为 (k+1)(3x+7)/(3x+7),所以整理为 1,所以此时结果为1
所以
当分母为合数，结果为0；当分母为素数，结果为1

代码如下:

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int mx=3e6+10;
int s[mx];
int isprime[mx];
void init()//这里初始化，求出每个i对应的数字是否为素数，然后求和
{ 
   
	memset(isprime,0,sizeof(isprime));
	for(int i=2;i<mx;i++)
	{ 
   
		if(!isprime[i])//最普通的埃氏筛法
		{ 
   
			for(int j=2*i;j<mx;j+=i)
			isprime[j]=1;
		}
	}
	memset(s,0,sizeof(s));
	s[0]=0,s[1]=0;
	for(int i=2;i<=1e6;i++)//求和
	{ 
   
		int re=3*i+7;
		s[i]=s[i-1]+(1-isprime[re]);
	}
}

int main()
{ 
   
	int t,n;
	init();
	scanf("%d",&t);
	while(t--)
	{ 
   
		scanf("%d",&n);
		printf("%d\n",s[n]);//直接输出
	}
	return 0;
}

今天的文章威尔逊定理B分享到此就结束了，感谢您的阅读。