需求

先简单描述溪源曾经遇到的需求：

需求一：项目结果文件中实验结论可能会存在未知类型、转换错误、空指针、超过索引长度等等。这里是类比需求，用日常开发中常出现的错误类型作为需求，如果要以上结论则判断这个项目检测失败；

解决方案一：
大家常用的方式可能是if(){continue;} esle if (){continue;} …或者switch-case等;

方案二：可能会使用集合contain()方法;

方案三：依次匹配字符串中字符（暴力匹配）；

以上两种方案都能解决；然后大家需要考虑性能、维护和代码整洁性，可能居多使用方案二；

需求二：项目结论中即存在正常、成功的结论，又存在以上列举的失败字段；

例如：

//存在异常错误
String str1 = "正常范围内;转换错误";

//存在异常错误
String str2 = "i=20空指针;超出索引长度;j正常";

//正常值
String str3 = "i=30;j值正常";

...等等

面对这种需求，大家可能会想到split()方法之后再判断是否正常等等…相信大家总是会有办法解决的。不再列举了，面对产品经理各种需求大家尽情发挥脑洞吧，那么开始进入今天的正题，溪源采用KMP字符串匹配算法解析此需求。

基础知识

根据上面介绍的需求，大家应该会对KMP算法解决的问题稍有理解。

KMP算法解决的问题：在字符串（主串）中是否能够定位出模式串（子串）。
上面提及到暴力匹配字符串，为什么不使用呢？时间复杂度O(m*n),而KMP算法时间复杂度为O(m+n)。

再介绍几个概念性的知识：

• 前缀：除最后一位以外，第一位依次与其余字符组成的字符串集合；

• 后缀：除第一位以外最后一位依次与其余字符组成的字符串集合；

简单举例：

字符串ABCD，其前缀：A,AB,ABC; 后缀：BCD,CD,D

• 部分匹配值：子串的前缀和后缀共有元素的长度。

简单举例：列举字符串ABCDABD的各个子串公共元素长度如下：

    -　"A"的前缀和后缀都为空集，共有元素的长度为0；

　　－　"AB"的前缀为[A]，后缀为[B]，共有元素的长度为0；

　　－　"ABC"的前缀为[A, AB]，后缀为[BC, C]，共有元素的长度0；

　　－　"ABCD"的前缀为[A, AB, ABC]，后缀为[BCD, CD, D]，共有元素的长度为0；

　　－　"ABCDA"的前缀为[A, AB, ABC, ABCD]，后缀为[BCDA, CDA, DA, A]，共有元素为"A"，长度为1；

　　－　"ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA]，后缀为[BCDAB, CDAB, DAB, AB, B]，共有元素为"AB"，长度为2；

　　－　"ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB]，后缀为[BCDABD, CDABD, DABD, ABD, BD, D]，共有元素的长度为0。

综上可以得出下面的表格：

逻辑解析

经历过上面的基础知识介绍后，下面开始一步步逻辑解析整个匹配过程：

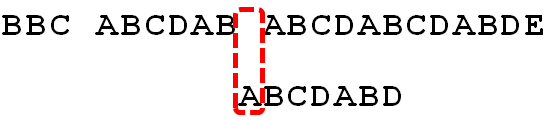
1. 字符串”BBC ABCDAB ABCDABCDABDE”的第一个字符与搜索串（模式串，以下简称P串）”ABCDABD”的第一个字符，进行比较。
   
2. 由于B与A字符不匹配，P串整体再往后移动一位与主串比较。
   
3. 此时主串第二位字符B与搜索串第一位A依然不匹配，P串再继续移动…，直至主串存在与P串第一个字符匹配。
   
4. 依次比较P串与主串的字符是否匹配。
   
5. 匹配过程中存在与主串存在不匹配字符。
   
6. 此时，大家应该是将P串再次整个后移一位，再从头逐个比较，如下图所示。虽然此种方式有效，但是效率很差，因为要把”搜索位置”移到已经比较过的位置，再次重比一遍。
   
7. 从5点可以明确知道，P串中字符D与主串空格不匹配时，其实字符D之前已经匹配的六个字符是已知的。因此KMP算法思想就是利用这个已知信息，不要重复比较已经比较过的位置，而是继续将P串向后移动几位。
   重点来了，向后移动几位呢？此时便用到了上面介绍的部分匹配表。

移动位数=已匹配的字符数-最后一个匹配字符对应的部分匹配值
因此，第5点之后，主串中空格与P串字符D字符不匹配时，已匹配字符为6个，最后一个以匹配字符B对应的部分匹配值为2，因此P串应该移动的位数为6-2=4。如图：

8. 空格与字符Ｃ不匹配，因此P串继续往后移。计算移动位数：已匹配的字符数为2（“AB”），对应的”部分匹配值”为0。所以，移动位数 = 2 – 0，结果为 2。

9. 空格与A不匹配，继续后移一位。

10. 逐位比较，直到发现C与D不匹配。于是，移动位数 = 6 – 2，继续将搜索词向后移动4位。

11. 逐位比较，直到搜索词的最后一位，发现完全匹配，于是搜索完成。如果还要继续搜索（即找出全部匹配），移动位数 = 7 – 0，再将搜索词向后移动7位，这里就不再重复了。

源码实现

public class Kmp { 
   
    /** * * @param originString 源字符串 * @param subString 子串 * @param next 部分匹配表, 是子串对应的部分匹配表 * @return 如果是-1 就是没有匹配到，否则返回第一个匹配的位置 */
    public static int kmpSearch(String originString, String subString, int[] next) { 
   
        for (int i = 0, j = 0; i < originString.length(); i++) { 
   
            while (j > 0 && originString.charAt(i) != subString.charAt(j)) { 
   
                j = next[j - 1];
            }

            if (originString.charAt(i) == subString.charAt(j)) { 
   
                j++;
            }
            if (j == subString.length()) { 
   
                return i - j + 1;
            }
        }
        return -1;
    }

    /** *获取到一个字符串(子串) 的部分匹配值表(前缀、后缀共同元素的长度) * @param dest 子串 * @return */
    public static int[] kmpNext(String dest) { 
   
        //创建一个 next 数组保存部分匹配值
        int[] next = new int[dest.length()];
        //如果字符串是长度为 1 部分匹配值就是 0
        next[0] = 0;
        for (int i = 1, j = 0; i < dest.length(); i++) { 
   
            while (j > 0 && dest.charAt(i) != dest.charAt(j)) { 
   
                j = next[j - 1];
            }
            //当 dest.charAt(i) == dest.charAt(j) 满足时，部分匹配值就是+1
            if(dest.charAt(i) == dest.charAt(j)) { 
   
                j++;
            }
            next[i] = j;
        }
        return next;
    }


    public static boolean matcherResult(String originString, List<String> unknownList) { 
   
        boolean unknown = false;
        for (String unknownConclusion : unknownList) { 
   
            int[] kmpNext = kmpNext(originString);
            int index = kmpSearch(originString, unknownConclusion, kmpNext);
            if (index != -1) { 
   
                unknown = true;
                break;
            }
        }
        return unknown;
    }

}

参考资料：http://jakeboxer.com/blog/2009/12/13/the-knuth-morris-pratt-algorithm-in-my-own-words/

今天的文章字符串匹配算法之KMP分享到此就结束了，感谢您的阅读。