机器学习中多分类模型的评估方法之–kappa系数

引言

分类是机器学习中监督学习的一种重要应用，基于统计的机器学习方法可以使用SVM进行二分类，可以使用决策书，梯度提升树等进行多分类。
对于二分类模型，我们通常可以使用ROC曲线来评估模型的预测效果。这里，我们介绍一下在多分类中衡量模型评估准确度的一种方法–kappa系数评估方法。

Kappa系数

首先，我们介绍一下kappa系数：
kappa系数是用在统计学中评估一致性的一种方法，我们可以用他来进行多分类模型准确度的评估，这个系数的取值范围是[-1,1]，实际应用中，一般是[0,1]，与ROC曲线中一般不会出现下凸形曲线的原理类似。
这个系数的值越高，则代表模型实现的分类准确度越高。kappa系数的计算方法可以这样来表示：

$$k=\dfrac{p_o-p_e}{1-p_e}$$

其中，p0表示为总的分类准确度;
pe表示为

$$p_e=\dfrac{a_1\times b_1+a_2\times b_2+...+a_C\times b_C}{n\times n}$$

其中，

$$a_i$$ 代表第i类真实样本个数，

$$b_i$$ 代表第i类预测出来的样本个数。

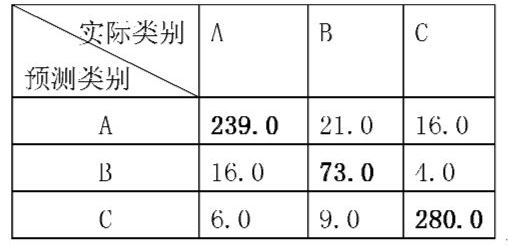
例子

例子数据来源:

https://blog.csdn.net/xtingjie/article/details/72803029

对于该表中的数据，则有：

$$p_o=\dfrac{239+73+280}{664}=0.8916$$

$$p_e=\dfrac{261\times 276+103\times 93 +300\times 295}{664\times 664}=0.3883$$

$$k=\dfrac{p_o-p_e}{1 - p_e}=\dfrac{0.8916-0.3883}{1-0.3883}=0.8228$$

代码

用python语言来实现，则有:

def kappa(matrix):
    n = np.sum(matrix)
    sum_po = 0
    sum_pe = 0
    for i in range(len(matrix[0])):
        sum_po += matrix[i][i]
        row = np.sum(matrix[i, :])
        col = np.sum(matrix[:, i])
        sum_pe += row * col
    po = sum_po / n
    pe = sum_pe / (n * n)
    # print(po, pe)
    return (po - pe) / (1 - pe)

其中，matrix是一个方阵，若共有i个类别，则matrix.shape = (i,i).
用下面的代码进行测试:

import numpy as np
matrix = [
    [239,21,16],
    [16,73,4]
    [6,9,280]]

matrix = np.array(matrix)
print(kappa(matrix))

今天的文章机器学习中多分类模型的评估方法之–kappa系数分享到此就结束了，感谢您的阅读。