从这一篇文章，你将要学到

如何利用griddata进行三维空间插值；
及其适用范围和进阶的逐步插值

背景

最近在做一个项目，要为上海市13000+个普通住宅楼盘算基本价格，俗称基价，可以从第三方来的案例数据只能覆盖大约3000个楼盘，余下的10000楼盘难为无米之炊，联想到地形图的思想，把上海市所有楼盘的基价看成海拔，楼盘的经纬度就是位置所在，然后会在三维空间形成一个连续平滑的三维曲面，这里利用scipy的interpolate类里面的griddata函数小试牛刀。

数据

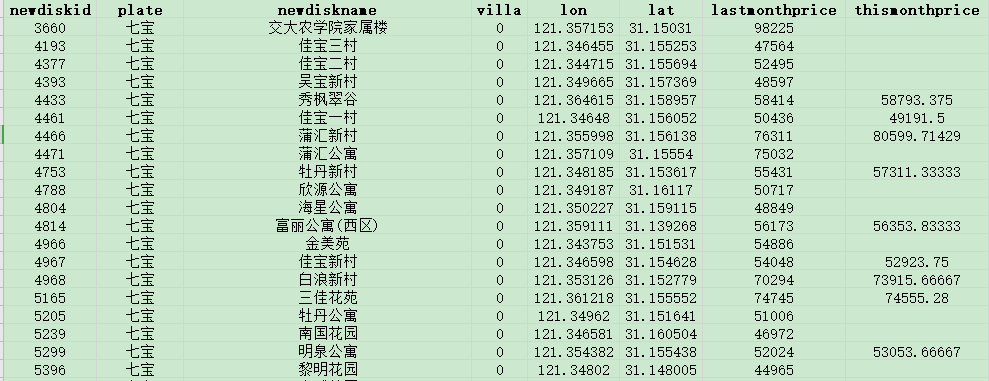
从原数据我们看到需要插值的thismonthprice有大量空缺，如何利用地理位置进行插值呢？基本思路如下

将数据分成两部分，一部分是thismonthprice有价格，一部分是thismonthprice为空的；
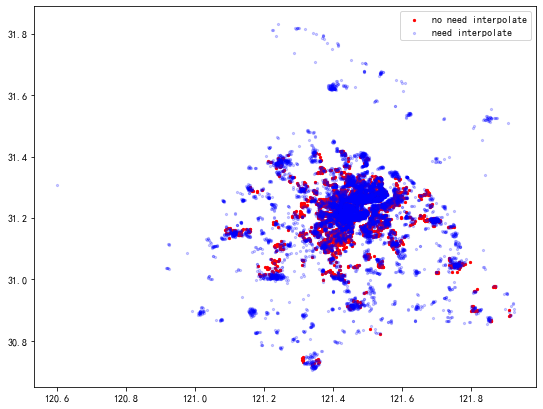
画出有价格和没价格的楼盘散点图，方便直观感受；
利用thismonthprice有价格的进行三维曲面建模训练；
利用训练好的模型对thismonthprice为空的进行模拟插值。

完整代码

import numpy as np #导入数值计算模块
import pandas as pd #导入数据分析模块
from scipy import stats
import matplotlib.pyplot as plt #导入绘图模块
from mpl_toolkits.mplot3d import Axes3D #导入3d绘图模块
from matplotlib import cm #颜色调整用
from scipy.interpolate import griddata #导入插值类

def scatterPlot(data): #绘制绘图函数
    plt.figure(figsize = (9, 7)) #新建画布
    caseData = data.dropna(subset = ["thismonthprice"]) #去掉空值,保留本月有价格的数据留作插值依据
    lon = caseData["lon"] #经度
    lat = caseData["lat"] #纬度
    
    interpolateData = data[data["thismonthprice"].isnull()] #待插值的数据
    x = interpolateData["lon"] #待插值的楼盘经度
    y = interpolateData["lat"] #待插值的楼盘纬度
    plt.scatter(lon, lat, s = 5, color = "r", label = "no need interpolate") #不需要插值的散点图
    plt.scatter(x, y, s = 5, color = "b", alpha = 0.2,  label = "need interpolate") #需要插值的散点图
    plt.legend()
    plt.show()

def gridInterpolate(data): #定义插值函数，data需要有newdiskid, lon,lat, 上个月价格，本月价格（有空缺）
    casenum = [] #用来存放有价格的楼盘数
    interpolatenum = [] #用来存放待插值的样本数
    caseData = data.dropna(subset = ["thismonthprice"]) #去掉空值,保留本月有价格的数据留作插值依据
    casenum.append(len(caseData)) #追加有价格的样本数
    casediskid = caseData["newdiskid"] #楼盘id
    lon = caseData["lon"] #经度
    lat = caseData["lat"] #纬度
    z = caseData["thismonthprice"] #价格
    
    interpolateData = data[data["thismonthprice"].isnull()] #待插值的数据
    interpolatenum.append(len(interpolateData)) #追加待插值样本数
    interpolatediskid = interpolateData["newdiskid"] #待插值的楼盘id
    x = interpolateData["lon"] #待插值的楼盘经度
    y = interpolateData["lat"] #待插值的楼盘纬度
    xx, yy = np.meshgrid(x, y) #平面网格点待插值的位置
    zz = griddata((lon, lat), z, (xx, yy), method='nearest', fill_value = z.median(), rescale = True) #stats.mode(z)[0][0]在没有价格的网格点插值
    Z = pd.DataFrame(zz) #数据框化

    interpolateprice = [] #用来存放插值
    for i in range(Z.shape[0]):
        interpolateprice.append(Z[i][i]) #取对角线上的元素
        
    label1 = pd.Series(np.zeros(len(casediskid))) #有价格的标签
    casedf = pd.concat([casediskid, z], axis = 1).reset_index()[["newdiskid", "thismonthprice"]] #索引重置
    casedf = pd.concat([casedf, label1], axis = 1)
    casedf.columns = ["newdiskid", "z", "label"]
    
    label2 = pd.Series(np.ones(len(interpolatediskid))) #插值标签
    interpolatedf = pd.DataFrame({ 
   "interpolatediskid":interpolatediskid, "interpolateprice": interpolateprice}).reset_index()[["interpolatediskid", "interpolateprice"]]
    interpolatedf = pd.concat([interpolatedf, label2], axis = 1)
    interpolatedf.columns = ["newdiskid", "z", "label"]    
    result = pd.concat([casedf, interpolatedf], ignore_index = True) #纵向拼接
    interpolateresult = pd.merge(data, result, how = "left") #匹配
    interpolateresult["diff"] = np.abs(interpolateresult["z"] - interpolateresult["lastmonthprice"])/interpolateresult["lastmonthprice"]  #绝对偏差率
    for i in range(len(interpolateresult)): #利用插值更新本月基价
        if interpolateresult["label"][i] == 1 and interpolateresult["diff"][i]< 0.05: #如果插值的绝对误差率小于0.05填补空缺价格
            interpolateresult["thismonthprice"][i] = interpolateresult["z"][i]
    interpolateresult.to_excel("无案例楼盘interpolateresult.xlsx")
    return casenum, interpolatenum, interpolateresult[["newdiskid","plate", "newdiskname", "villa", "lon", "lat", "lastmonthprice", "thismonthprice"]] #返回更新本月基价的数据框

if __name__ == "__main__":
    data = pd.read_excel("无案例楼盘逐步插值.xlsx") #读取数据
    scatterPlot(data)
    casenum, interpolatenum, data = gridInterpolate(data)

代码解读

主要由scatterPlot和gridInterpolate两个函数实现，
其中scatterPlot主要负责绘制散点图，图片如下

gridInterpolate主要负责插值功能

griddata基本调用格式如下

scipy.interpolate.griddata（points，values，xi，method ='linear'，fill_value = nan，rescale = False ）

points
数据点坐标。可以是形状（n，D）的数组，也可以是ndim数组的元组。
values
浮点或复数的ndarray，形状（n，）的数据值
xi

浮点数的二维数组或一维数组的元组，形状（M，D）插值数据的点。

method

可选插值方法。{‘linear’，‘nearest’，‘cubic’}，之一，其中
linear 将输入点设置为n维单纯形，并在每个单形上线性插值，可以简单理解为以三角形为基础，就是按Delaunay方法先找出内插点四周的3个点,构成三角形,内插点在三角形内.然后线性内插,或三次方程内插.。
nearest 返回最接近插值点的数据点的值。
cubic 返回由三次样条确定的值。返回由分段立方，连续可微（C1）和近似曲率最小化多项式表面确定的值。

fill_value
float，可选，用于填充输入点凸包外部的请求点的值，如果未提供，则默认为nan。此选项对“最近”方法无效。
rescale
bool，可选，在执行插值之前，重新缩放指向单位立方体，如果某些输入维度具有不可比较的单位并且相差很多个数量级。

逐步插值

插值是一个逐步扩散的过程，如果让第一次插值的结果再参与训练的话，第二次插值效果会好一些，以此类推，循环下去，就可以逐步插值，最后会达到一种收敛状态，所以需要用一个标志其达到收敛了，最简单的判断方式就是插值数据不再提升了就认为收敛了。

# -*- coding: utf-8 -*-
""" Project_name:逐步插值 Description:多次插值实现无案例楼盘基价赋值 Created on Tue Oct 20 17:59:08 2020 @author: 帅帅de三叔 """
import numpy as np #导入数值计算模块
import pandas as pd #导入数据分析模块
from scipy import stats
import matplotlib.pyplot as plt #导入绘图模块
from mpl_toolkits.mplot3d import Axes3D #导入3d绘图模块
from matplotlib import cm #颜色调整用
from scipy.interpolate import griddata #导入插值类

def scatterPlot(data): #绘制绘图函数
    plt.figure(figsize = (9, 7)) #新建画布
    caseData = data.dropna(subset = ["thismonthprice"]) #去掉空值,保留本月有价格的数据留作插值依据
    lon = caseData["lon"] #经度
    lat = caseData["lat"] #纬度
    
    interpolateData = data[data["thismonthprice"].isnull()] #待插值的数据
    x = interpolateData["lon"] #待插值的楼盘经度
    y = interpolateData["lat"] #待插值的楼盘纬度
    plt.scatter(lon, lat, s = 5, color = "r", label = "no need interpolate") #不需要插值的散点图
    plt.scatter(x, y, s = 5, color = "b", alpha = 0.2,  label = "need interpolate") #需要插值的散点图
    plt.legend()
    plt.show()

def gridInterpolate(data): #定义插值函数，data需要有newdiskid, lon,lat, 上个月价格，本月价格（有空缺）
    casenum = [] #用来存放有价格的楼盘数
    interpolatenum = [] #用来存放待插值的样本数
    caseData = data.dropna(subset = ["thismonthprice"]) #去掉空值,保留本月有价格的数据留作插值依据
    casenum.append(len(caseData)) #追加有价格的样本数
    casediskid = caseData["newdiskid"] #楼盘id
    lon = caseData["lon"] #经度
    lat = caseData["lat"] #纬度
    z = caseData["thismonthprice"] #价格
    
    interpolateData = data[data["thismonthprice"].isnull()] #待插值的数据
    interpolatenum.append(len(interpolateData)) #追加待插值样本数
    interpolatediskid = interpolateData["newdiskid"] #待插值的楼盘id
    x = interpolateData["lon"] #待插值的楼盘经度
    y = interpolateData["lat"] #待插值的楼盘纬度
    xx, yy = np.meshgrid(x, y) #平面网格点待插值的位置
    zz = griddata((lon, lat), z, (xx, yy), method='nearest', fill_value = z.median(), rescale = True) #stats.mode(z)[0][0]在没有价格的网格点插值
    Z = pd.DataFrame(zz) #数据框化

    interpolateprice = [] #用来存放插值
    for i in range(Z.shape[0]):
        interpolateprice.append(Z[i][i]) #取对角线上的元素
        
    label1 = pd.Series(np.zeros(len(casediskid))) #有价格的标签
    casedf = pd.concat([casediskid, z], axis = 1).reset_index()[["newdiskid", "thismonthprice"]] #索引重置
    casedf = pd.concat([casedf, label1], axis = 1)
    casedf.columns = ["newdiskid", "z", "label"]
    
    label2 = pd.Series(np.ones(len(interpolatediskid))) #插值标签
    interpolatedf = pd.DataFrame({ 
   "interpolatediskid":interpolatediskid, "interpolateprice": interpolateprice}).reset_index()[["interpolatediskid", "interpolateprice"]]
    interpolatedf = pd.concat([interpolatedf, label2], axis = 1)
    interpolatedf.columns = ["newdiskid", "z", "label"]    
    result = pd.concat([casedf, interpolatedf], ignore_index = True) #纵向拼接
    interpolateresult = pd.merge(data, result, how = "left") #匹配
    interpolateresult["diff"] = np.abs(interpolateresult["z"] - interpolateresult["lastmonthprice"])/interpolateresult["lastmonthprice"]  #绝对偏差率
    for i in range(len(interpolateresult)): #利用插值更新本月基价
        if interpolateresult["label"][i] == 1 and interpolateresult["diff"][i]< 0.05: #如果插值的绝对误差率小于0.05填补空缺价格
            interpolateresult["thismonthprice"][i] = interpolateresult["z"][i]
    interpolateresult.to_excel("无案例楼盘interpolateresult.xlsx")
    return casenum, interpolatenum, interpolateresult[["newdiskid","plate", "newdiskname", "villa", "lon", "lat", "lastmonthprice", "thismonthprice"]] #返回更新本月基价的数据框

if __name__ == "__main__":
    data = pd.read_excel("无案例楼盘逐步插值.xlsx") #读取数据
    scatterPlot(data)
    casenum, interpolatenum, data = gridInterpolate(data)
    print(casenum[-1], len(data.dropna(subset = ["thismonthprice"])))
    for i in range(10):
        if casenum[-1] < len(data.dropna(subset = ["thismonthprice"])): #未收敛则继续插值
            casenum, interpolatenum, data = gridInterpolate(data)
            scatterPlot(data)
            print(casenum[-1], len(data.dropna(subset = ["thismonthprice"])))

插值动态图如下，从动图可以看到需要插值的越来越少，即图中的蓝色的越来越少，反观红色的越来越多。

总结

插值还是很消耗资源的，所以比较慢，用3000个插值10000个，有种四两拨千斤的感觉，最后效果不会特别好，比如插值到收敛了一共插值出6000个，相当于填补了一部分数据标签，这为以后的机器学习模型提供了基础。

参考文献

1, 空间坐标和坐标所对应的属性（高程，温度等）https://blog.csdn.net/csubai07/article/details/104344291

2, griddata用法 https://blog.csdn.net/gxf0789/article/details/82384372

3, griddata 原理 http://blog.sina.com.cn/s/blog_6264e23a01016k9f.html

4, matlab 的griddata https://www.mathworks.com/help/matlab/ref/griddata.html

5, Scipy 的插值 http://liao.cpython.org/scipytutorial11/

6,（数值分析）各种插值法的python实现 https://blog.csdn.net/qq_20011607/article/details/81412985
7，https://blog.csdn.net/weixin_43718675/article/details/103497930?utm_medium=distribute.pc_aggpage_search_result.none-task-blog-2_allsobaiduend~default-1-103497930.nonecase&utm_term=python%E4%B8%ADgriddata%E5%87%BD%E6%95%B0&spm=1000.2123.3001.4430

今天的文章griddata三维空间插值分享到此就结束了，感谢您的阅读。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容，请发送邮件至举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/4860.html

griddata三维空间插值

背景

数据

完整代码

代码解读

逐步插值

总结

参考文献

相关推荐

发表回复