本编博客会谈谈图像滤波,会分别写出滤波过程和原理;
主要可分为以下两大类:
一、线性滤波
1、均值滤波blur()
2、方框滤波 boxFilter()
3、高斯滤波GaussianBlur()
二、非线性滤波
1、中值滤波medianBlur()–当滤波核尺寸大于5时,输入图像只能是CV_8U格式的。
2、双边滤波bilateralFilter()
在前面学习边沿检测时,当时就遇到过滤波的问题,现在开始学习一下主要的原理
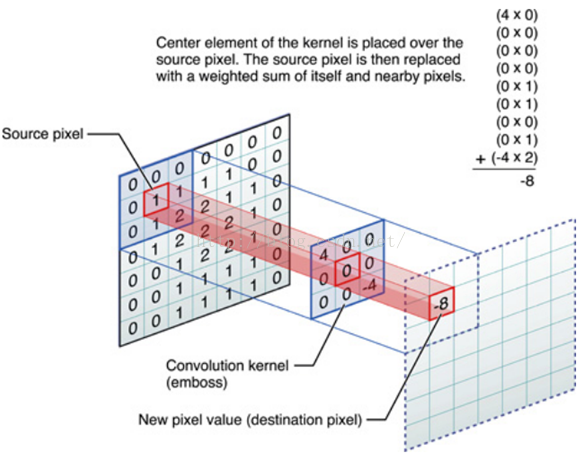
图像的空域线性滤波和非线性滤波在空域对图像进行滤波处理无非两种情况,线性滤波和非线性滤波。滤波的意思就是对原图像的每个像素周围一定范围内的像素进行运算,运算的范围就称为掩膜或领域。而运算就分两种了,如果运算只是对各像素灰度值进行简单处理(如乘一个权值)最后求和,就称为线性滤波;而如果对像素灰度值的运算比较复杂,而不是最后求和的简单运算,则是非线性滤波;如求一个像素周围3×3范围内最大值、最小值、中值、均值等操作都不是简单的加权,都属于非线性滤波。
图像滤波既可以在实域进行,也可以在频域进行。图像滤波可以更改或者增强图像。通过滤波,可以强调一些特征或者去除图像中一些不需要的部分。滤波是一个邻域操作算子,利用给定像素周围的像素的值决定此像素的最终的输出值。
(i,j)是像素在图片中的位置;
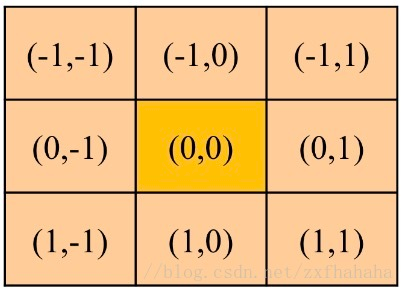
(m,n)是卷积核中的位置/坐标,其中心点的坐标是(0,0) ;
k(m,n)是卷积核中在(m, n)上的权重参数
I[i+m, j+n]是与k(m,n)相对应的图片像素值
O(i,j)是图片中(i,j)像素的滤波/卷积结果
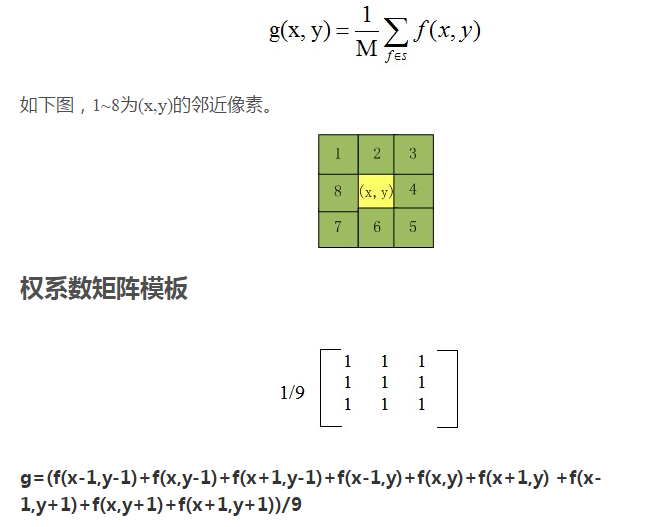
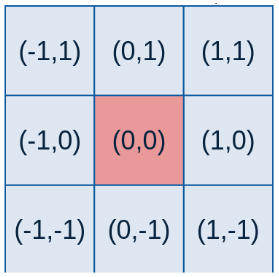
如下图,当i,j=0时,也就是中心位置是(0,0)。此位置的邻域就是加减m和n, 当m,n=1时(0,0)的邻域就是下面的9个位置。
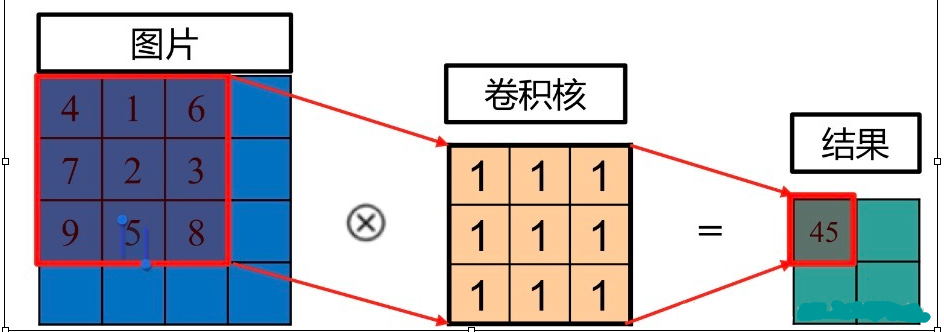
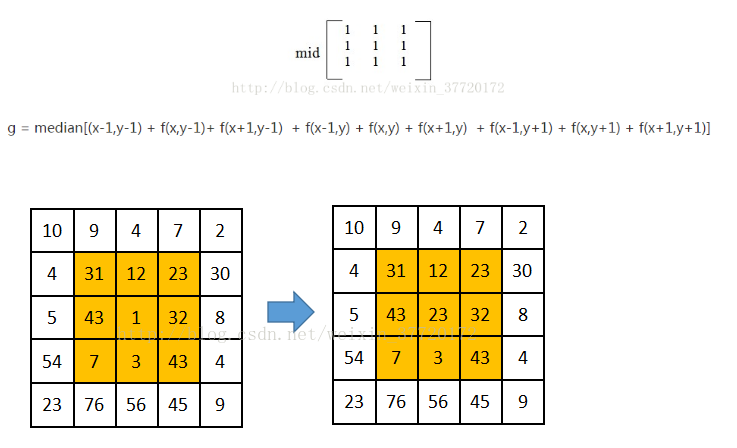
卷积的操作如下图所示,图片上圈的红框就是卷积核要操作的邻域。例子中卷积核每个位置上的值都为1,因此进行卷积就是把图片上的9个值分别乘上对应卷积核上的值1再求和,4*1+1*1+6*1+7*1+2*1+3*1+9*1+5*1+8*1=45。 其中,45对应卷积核中间1对应的位置;
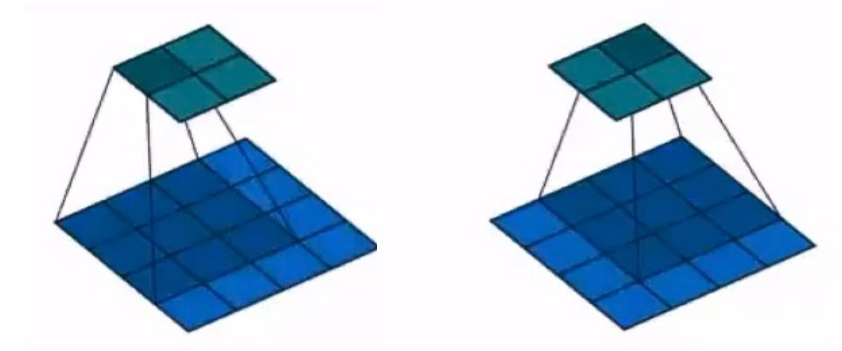
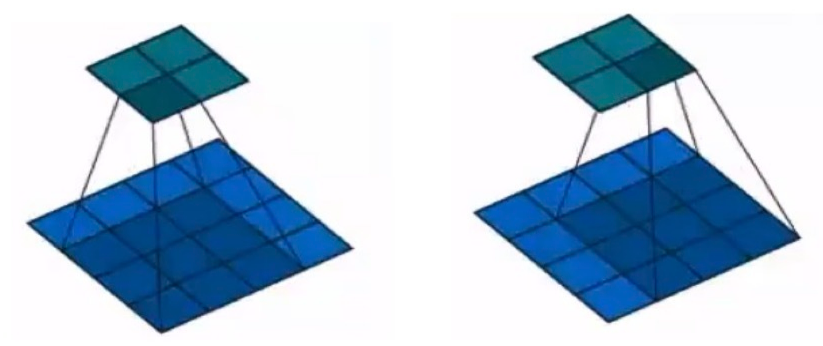
上面是卷积核移动得到对应的2×2的矩阵结果。
也可以看看这个图理解一下卷积核效果:
边界补充
由上面介绍的卷积操作可以看出,结果比原来图像小了,那么如果要获得同尺寸输出,则要进行边界补充。 因为卷积核越大,得到的结果就越少,所以要补充的就越多。
那进行补充的值为多少呢,下面将介绍4中补充的类型。
我们以7×7卷积:3×3补充成9×9为例。
补零(zero-padding)
补零很简单,就是把缺失的地方都补成0 。
关于卷积核的相关知识可以参考博文:https://blog.csdn.net/zouxy09/article/details/49080029和https://www.cnblogs.com/zgy-personal/p/7227872.html
关于边界补充的相关知识可以参考博文:https://blog.csdn.net/zxfhahaha/article/details/80139430
滤波函数简介
均值滤波:
均值滤波方法是,对待处理的当前像素,选择一个模板,该模板为其邻近的若干个像素组成,用模板的均值来替代原像素的值的方法。
方法优缺点
优点:算法简单,计算速度快;
缺点:降低噪声的同时使图像产生模糊,特别是景物的边缘和细节部分。
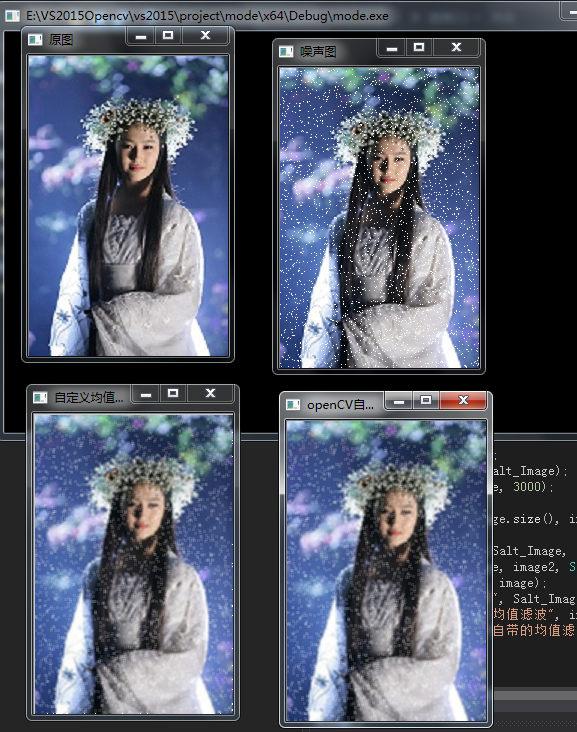
下面为实现均值滤波的代码和结果
#include "opencv2/imgproc.hpp" #include "opencv2/highgui.hpp" #include<ctime> using namespace cv; using namespace std; //均值滤波 void AverFiltering(const Mat &src, Mat &dst) { if (!src.data) return; //at访问像素点 for (int i = 1; i<src.rows; ++i) for (int j = 1; j < src.cols; ++j) { if ((i - 1 >= 0) && (j - 1) >= 0 && (i + 1)<src.rows && (j + 1)<src.cols) {//边缘不进行处理 dst.at<Vec3b>(i, j)[0] = (src.at<Vec3b>(i, j)[0] + src.at<Vec3b>(i - 1, j - 1)[0] + src.at<Vec3b>(i - 1, j)[0] + src.at<Vec3b>(i, j - 1)[0] + src.at<Vec3b>(i - 1, j + 1)[0] + src.at<Vec3b>(i + 1, j - 1)[0] + src.at<Vec3b>(i + 1, j + 1)[0] + src.at<Vec3b>(i, j + 1)[0] + src.at<Vec3b>(i + 1, j)[0]) / 9; dst.at<Vec3b>(i, j)[1] = (src.at<Vec3b>(i, j)[1] + src.at<Vec3b>(i - 1, j - 1)[1] + src.at<Vec3b>(i - 1, j)[1] + src.at<Vec3b>(i, j - 1)[1] + src.at<Vec3b>(i - 1, j + 1)[1] + src.at<Vec3b>(i + 1, j - 1)[1] + src.at<Vec3b>(i + 1, j + 1)[1] + src.at<Vec3b>(i, j + 1)[1] + src.at<Vec3b>(i + 1, j)[1]) / 9; dst.at<Vec3b>(i, j)[2] = (src.at<Vec3b>(i, j)[2] + src.at<Vec3b>(i - 1, j - 1)[2] + src.at<Vec3b>(i - 1, j)[2] + src.at<Vec3b>(i, j - 1)[2] + src.at<Vec3b>(i - 1, j + 1)[2] + src.at<Vec3b>(i + 1, j - 1)[2] + src.at<Vec3b>(i + 1, j + 1)[2] + src.at<Vec3b>(i, j + 1)[2] + src.at<Vec3b>(i + 1, j)[2]) / 9; } else {//边缘赋值 dst.at<Vec3b>(i, j)[0] = src.at<Vec3b>(i, j)[0]; dst.at<Vec3b>(i, j)[1] = src.at<Vec3b>(i, j)[1]; dst.at<Vec3b>(i, j)[2] = src.at<Vec3b>(i, j)[2]; } } } //图像椒盐化 void salt(Mat &image, int num) { if (!image.data) return;//防止传入空图 int i, j; srand(time(NULL)); for (int x = 0; x < num; ++x) { i = rand() % image.rows; j = rand() % image.cols; image.at<Vec3b>(i, j)[0] = 255; image.at<Vec3b>(i, j)[1] = 255; image.at<Vec3b>(i, j)[2] = 255; } } void main() { Mat image = imread("E:\\VS2015Opencv\\vs2015\\project\\picture\\01.jpg"); Mat Salt_Image; image.copyTo(Salt_Image); salt(Salt_Image, 3000); Mat image1(image.size(), image.type()); Mat image2; AverFiltering(Salt_Image, image1); blur(Salt_Image, image2, Size(3, 3));//openCV库自带的均值滤波函数 imshow("原图", image); imshow("噪声图", Salt_Image); imshow("自定义均值滤波", image1); imshow("openCV自带的均值滤波", image2); waitKey(); }
方框滤波:原理与均值滤波类似
opencv中boxFilter函数的作用是使用方框滤波(box filter)来模糊一张图片。
方框滤波算法的原理很简单,指定一个X*Y的矩阵大小,目标像素的周围X*Y矩阵内的像素全部相加作为目标像素的值,就这么简单.
Boxfilter的初始化过程如下:
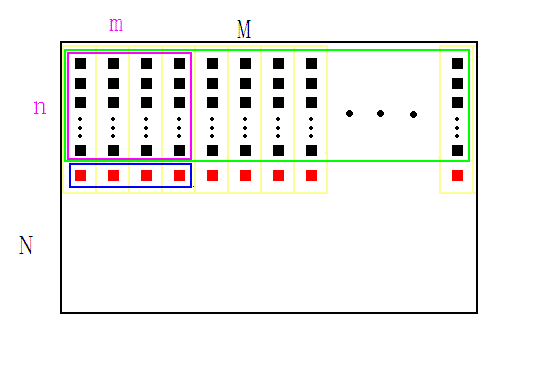
1、给定一张图像,宽高为(M,N),确定待求矩形模板的宽高(m,n),如图紫色矩形。图中每个黑色方块代表一个像素,红色方块是假想像素。
2、开辟一段大小为M的数组,记为buff, 用来存储计算过程的中间变量,用红色方块表示
3、将矩形模板(紫色)从左上角(0,0)开始,逐像素向右滑动,到达行末时,矩形移动到下一行的开头(0,1),如此反复,每移动到一个新位置时,计算矩形内的像素和,保存在数组A中。以(0,0)位置为例进行说明:首先将绿色矩形内的每一列像素求和,结果放在buff内(红色方块),再对蓝色矩形内的像素求和,结果即为紫色特征矩形内的像素和,把它存放到数组A中,如此便完成了第一次求和运算。
4、每次紫色矩形向右移动时,实际上就是求对应的蓝色矩形的像素和,此时只要把上一次的求和结果减去蓝色矩形内的第一个红色块,再加上它右面的一个红色块,就是当前位置的和了,用公式表示 sum[i] = sum[i-1] – buff[x-1] + buff[x+m-1]
5、当紫色矩形移动到行末时,需要对buff进行更新。因为整个绿色矩形下移了一个像素,所以对于每个buff[i], 需要加上一个新进来的像素,再减去一个出去的像素,然后便开始新的一行的计算了。
代码如下:
#include <iostream>
#include <opencv2/core.hpp>
#include <opencv2/highgui.hpp>
#include <opencv2/imgproc.hpp>
/////////////////////////////////////////
//求积分图-优化方法
//由上方negral(i-1,j)加上当前行的和即可
//对于W*H图像:2*(W-1)*(H-1)次加减法
//比常规方法快1.5倍左右
/////////////////////////////////////////
void Fast_integral(cv::Mat& src, cv::Mat& dst) {
int nr = src.rows;
int nc = src.cols;
int sum_r = 0;
dst = cv::Mat::zeros(nr + 1, nc + 1, CV_64F);
for (int i = 1; i < dst.rows; ++i) {
for (int j = 1, sum_r = 0; j < dst.cols; ++j) {
//行累加,因为积分图相当于在原图上方加一行,左边加一列,所以积分图的(1,1)对应原图(0,0),(i,j)对应(i-1,j-1)
sum_r = src.at<uchar>(i - 1, j - 1) + sum_r; //行累加
dst.at<double>(i, j) = dst.at<double>(i - 1, j) + sum_r;
}
}
}
//////////////////////////////////
//盒子滤波-均值滤波是其特殊情况
/////////////////////////////////
void BoxFilter(cv::Mat& src, cv::Mat& dst, cv::Size wsize, bool normalize) {
//图像边界扩充
if (wsize.height % 2 == 0 || wsize.width % 2 == 0) {
fprintf(stderr, "Please enter odd size!");
exit(-1);
}
int hh = (wsize.height - 1) / 2;
int hw = (wsize.width - 1) / 2;
cv::Mat Newsrc;
cv::copyMakeBorder(src, Newsrc, hh, hh, hw, hw, cv::BORDER_REFLECT);//以边缘为轴,对称
src.copyTo(dst);
//计算积分图
cv::Mat inte;
Fast_integral(Newsrc, inte);
//BoxFilter
double mean = 0;
for (int i = hh + 1; i < src.rows + hh + 1; ++i) { //积分图图像比原图(边界扩充后的)多一行和一列
for (int j = hw + 1; j < src.cols + hw + 1; ++j) {
double top_left = inte.at<double>(i - hh - 1, j - hw - 1);
double top_right = inte.at<double>(i - hh - 1, j + hw);
double buttom_left = inte.at<double>(i + hh, j - hw - 1);
double buttom_right = inte.at<double>(i + hh, j + hw);
if (normalize == true)
mean = (buttom_right - top_right - buttom_left + top_left) / wsize.area();
else
mean = buttom_right - top_right - buttom_left + top_left;
//一定要进行判断和数据类型转换
if (mean < 0)
mean = 0;
else if (mean>255)
mean = 255;
dst.at<uchar>(i - hh - 1, j - hw - 1) = static_cast<uchar>(mean);
}
}
}
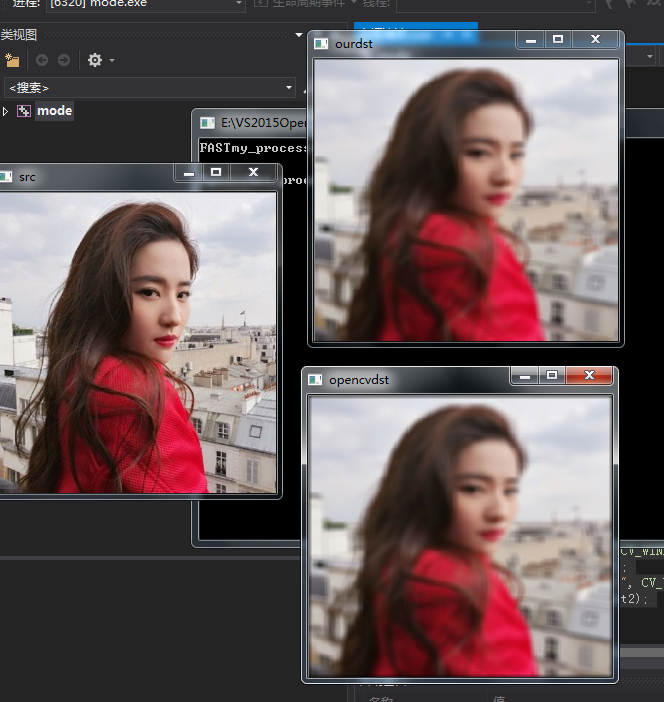
int main() {
cv::Mat src = cv::imread("E:\\VS2015Opencv\\vs2015\\project\\picture\\06.jpg");
if (src.empty()) {
return -1;
}
//自编BoxFilter测试
cv::Mat dst1;
double t2 = (double)cv::getTickCount(); //测时间
if (src.channels() > 1) {
std::vector<cv::Mat> channel;
cv::split(src, channel);
BoxFilter(channel[0], channel[0], cv::Size(7, 7), true);//盒子滤波
BoxFilter(channel[1], channel[1], cv::Size(7, 7), true);//盒子滤波
BoxFilter(channel[2], channel[2], cv::Size(7, 7), true);//盒子滤波
cv::merge(channel, dst1);
}
else
BoxFilter(src, dst1, cv::Size(7, 7), true);//盒子滤波
t2 = (double)cv::getTickCount() - t2;
double time2 = (t2 *1000.) / ((double)cv::getTickFrequency());
std::cout << "FASTmy_process=" << time2 << " ms. " << std::endl << std::endl;
//opencv自带BoxFilter测试
cv::Mat dst2;
double t1 = (double)cv::getTickCount(); //测时间
cv::boxFilter(src, dst2, -1, cv::Size(7, 7), cv::Point(-1, -1), true, cv::BORDER_CONSTANT);//盒子滤波
t1 = (double)cv::getTickCount() - t1;
double time1 = (t1 *1000.) / ((double)cv::getTickFrequency());
std::cout << "Opencvbox_process=" << time1 << " ms. " << std::endl << std::endl;
cv::namedWindow("src");
cv::imshow("src", src);
cv::namedWindow("ourdst", CV_WINDOW_NORMAL);
cv::imshow("ourdst", dst1);
cv::namedWindow("opencvdst", CV_WINDOW_NORMAL);
cv::imshow("opencvdst", dst2);
cv::waitKey(0);
}
高斯滤波:
关于高斯函数和滤波可以参考这边博文:https://blog.csdn.net/jgj123321/article/details/94448463和https://www.cnblogs.com/qiqibaby/p/5289977.html
高斯滤波原理及离散化
现在主要讲解一下原理:
要产生一个3×3的高斯滤波器模板,以模板的中心位置为坐标原点进行取样。模板在各个位置的坐标,如下所示(x轴水平向右,y轴竖直向下)。
其中(x,y)为点坐标,在图像处理中可认为是整数,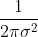
注意:由于最后要进行归一化处理,因此在计算模板中各个元素的值时,可以去掉高斯函数的系数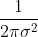
通过上述的实现过程发现,生成高斯滤波器模板最重要的参数就是高斯分布的标准差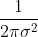
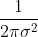
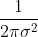
根据上面原理我们可以得到高斯模板的代码公式:
二维高斯模板的生成:
double **getTwoGuassionArray(int size, double sigma) { double sum = 0.0; int kerR = size / 2; double **arr = new double*[size]; for (int i = 0; i < size; i++) { arr[i] = new double[size]; } for (int i = 0; i < size; i++) { for (int j = 0; j < size; j++) { arr[i][j] = exp(-((i-kerR)*(i-kerR) + (j-kerR)*(j-kerR)) / (2 * sigma*sigma)); sum += arr[i][j]; } } for (int i = 0; i < size; i++) { for (int j = 0; j < size; j++) { arr[i][j] /= sum; cout << arr[i][j] << endl; } } return arr; }
一维高斯模板的生成:
double *getOneGuassionArray(int size, double sigma) { double sum = 0.0; int kerR = size / 2; double *arr = new double[size]; for (int i = 0; i < size; i++) { arr[i] = exp(-((i - kerR)*(i - kerR)) / (2 * sigma*sigma)); sum += arr[i]; } for (int i = 0; i < size; i++) { arr[i] /= sum; cout << arr[i] << endl; } return arr; }
具体实现代码:
#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/highgui/highgui.hpp"
#include <iostream>
#include <cmath>
using namespace cv;
using namespace std;
double **getTwoGuassionArray(int size, double sigma) {
double sum = 0.0;
int kerR = size / 2;
double **arr = new double*[size];
for (int i = 0; i < size; i++)
{
arr[i] = new double[size];
}
for (int i = 0; i < size; i++)
{
for (int j = 0; j < size; j++)
{
arr[i][j] = exp(-((i - kerR)*(i - kerR) + (j - kerR)*(j - kerR)) / (2 * sigma*sigma));
sum += arr[i][j];
}
}
for (int i = 0; i < size; i++)
{
for (int j = 0; j < size; j++)
{
arr[i][j] /= sum;
cout << arr[i][j] << endl;
}
}
return arr;
}
void MyGaussianBlur(Mat &srcImage, Mat &dst, int size)
{
CV_Assert(srcImage.channels() || srcImage.channels() == 3);
int kerR = size / 2;
dst = srcImage.clone();
int channels = dst.channels();
double** arr;
arr = getTwoGuassionArray(size, 1);
for (int i = kerR; i < dst.rows - kerR; i++)
{
for (int j = kerR; j < dst.cols - kerR; j++)
{
double GuassionSum[3] = { 0 };
for (int k = -kerR; k <= kerR; k++)
{
for (int n = -kerR; n <= kerR; n++)
{
if (channels == 1)
{
GuassionSum[0] += arr[kerR + k][kerR + n] * dst.at<uchar>(i + k, j + n);
}
else if (channels == 3)
{
Vec3b bgr = dst.at<Vec3b>(i + k, j + n);
auto a = arr[kerR + k][kerR + n];
GuassionSum[0] += a*bgr[0];
GuassionSum[1] += a*bgr[1];
GuassionSum[2] += a*bgr[2];
}
}
}
for (int k = 0; k < channels; k++)
{
if (GuassionSum[k] < 0)
GuassionSum[k] = 0;
else if (GuassionSum[k] > 255)
GuassionSum[k] = 255;
}
if (channels == 1)
dst.at<uchar>(i, j) = static_cast<uchar>(GuassionSum[0]);
else if (channels == 3)
{
Vec3b bgr = { static_cast<uchar>(GuassionSum[0]), static_cast<uchar>(GuassionSum[1]), static_cast<uchar>(GuassionSum[2]) };
dst.at<Vec3b>(i, j) = bgr;
}
}
}
for (int i = 0; i < size; i++)
delete[] arr[i];
delete[] arr;
}
int main()
{
Mat srcImage = imread("E:\\VS2015Opencv\\vs2015\\project\\picture\\06.jpg");
if (!srcImage.data)
{
printf("could not load image...\n");
return -1;
}
//getGuassionArray(3, 1);
Mat resMat;
MyGaussianBlur(srcImage, resMat, 3);
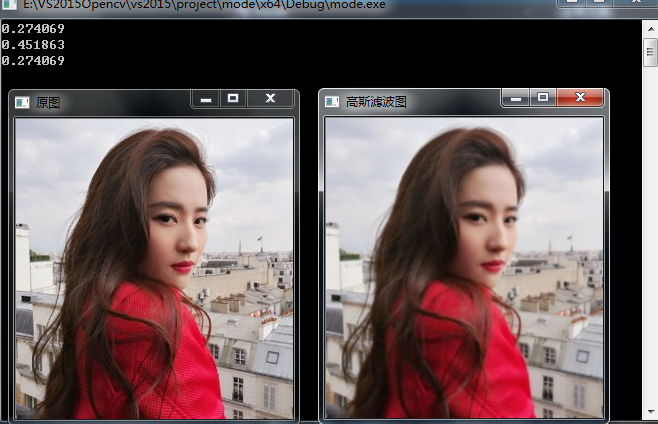
imshow("原图", srcImage);
imshow("高斯滤波图", resMat);
waitKey(0);
return 0;
}
只处理单通道或者三通道图像,模板生成后,其滤波(卷积过程)就比较简单了。不过,这样的高斯滤波过程,其循环运算次数为,其中m,n为图像的尺寸;ksize为高斯滤波器的尺寸。这样其时间复杂度为,随滤波器的模板的尺寸呈平方增长,当高斯滤波器的尺寸较大时,其运算效率是极低的。为了,提高滤波的运算速度,可以将二维的高斯滤波过程分解开来。
分离实现高斯滤波
由于高斯函数的可分离性,尺寸较大的高斯滤波器可以分成两步进行:首先将图像在水平(竖直)方向与一维高斯函数进行卷积;然后将卷积后的结果在竖直(水平)方向使用相同的一维高斯函数得到的模板进行卷积运算。具体实现代码如下:
#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/highgui/highgui.hpp"
#include <iostream>
#include <cmath>
using namespace cv;
using namespace std;
double *getOneGuassionArray(int size, double sigma)
{
double sum = 0.0;
int kerR = size / 2;
double *arr = new double[size];
for (int i = 0; i < size; i++)
{
arr[i] = exp(-((i - kerR)*(i - kerR)) / (2 * sigma*sigma));
sum += arr[i];
}
for (int i = 0; i < size; i++)
{
arr[i] /= sum;
cout << arr[i] << endl;
}
return arr;
}
void MyGaussianBlur(Mat &srcImage, Mat &dst, int size)
{
CV_Assert(srcImage.channels() || srcImage.channels() == 3);
int kerR = size / 2;
dst = srcImage.clone();
int channels = dst.channels();
double* arr;
arr = getOneGuassionArray(size, 1);
for (int i = kerR; i < dst.rows - kerR; i++)
{
for (int j = kerR; j < dst.cols - kerR; j++)
{
double GuassionSum[3] = { 0 };
for (int k = -kerR; k <= kerR; k++)
{
if (channels == 1)
{
GuassionSum[0] += arr[kerR + k] * dst.at<uchar>(i, j + k);
}
else if (channels == 3)
{
Vec3b bgr = dst.at<Vec3b>(i, j + k);
auto a = arr[kerR + k];
GuassionSum[0] += a*bgr[0];
GuassionSum[1] += a*bgr[1];
GuassionSum[2] += a*bgr[2];
}
}
for (int k = 0; k < channels; k++)
{
if (GuassionSum[k] < 0)
GuassionSum[k] = 0;
else if (GuassionSum[k] > 255)
GuassionSum[k] = 255;
}
if (channels == 1)
dst.at<uchar>(i, j) = static_cast<uchar>(GuassionSum[0]);
else if (channels == 3)
{
Vec3b bgr = { static_cast<uchar>(GuassionSum[0]), static_cast<uchar>(GuassionSum[1]), static_cast<uchar>(GuassionSum[2]) };
dst.at<Vec3b>(i, j) = bgr;
}
}
}
for (int i = kerR; i < dst.rows - kerR; i++)
{
for (int j = kerR; j < dst.cols - kerR; j++)
{
double GuassionSum[3] = { 0 };
for (int k = -kerR; k <= kerR; k++)
{
if (channels == 1)
{
GuassionSum[0] += arr[kerR + k] * dst.at<uchar>(i + k, j);
}
else if (channels == 3)
{
Vec3b bgr = dst.at<Vec3b>(i + k, j);
auto a = arr[kerR + k];
GuassionSum[0] += a*bgr[0];
GuassionSum[1] += a*bgr[1];
GuassionSum[2] += a*bgr[2];
}
}
for (int k = 0; k < channels; k++)
{
if (GuassionSum[k] < 0)
GuassionSum[k] = 0;
else if (GuassionSum[k] > 255)
GuassionSum[k] = 255;
}
if (channels == 1)
dst.at<uchar>(i, j) = static_cast<uchar>(GuassionSum[0]);
else if (channels == 3)
{
Vec3b bgr = { static_cast<uchar>(GuassionSum[0]), static_cast<uchar>(GuassionSum[1]), static_cast<uchar>(GuassionSum[2]) };
dst.at<Vec3b>(i, j) = bgr;
}
}
}
delete[] arr;
}
int main()
{
Mat srcImage = imread("E:\\VS2015Opencv\\vs2015\\project\\picture\\06.jpg");
if (!srcImage.data)
{
printf("could not load image...\n");
return -1;
}
//getGuassionArray(3, 1);
Mat resMat;
MyGaussianBlur(srcImage, resMat, 3);
imshow("原图", srcImage);
imshow("高斯滤波图", resMat);
waitKey(0);
return 0;
}
中值滤波
首先,我们复习中值。在一连串数字{1,4,6,8,9}中,数字6就是这串数字的中值。由此我们可以应用到图像处理中。依然我们在图像中去3*3的矩阵,里面有9个像素点,我们将9个像素进行排序,最后将这个矩阵的中心点赋值为这九个像素的中值。
所以说,中值滤波原理很简单,就是排大小的问题
中值滤波法对消除椒盐噪声非常有效,在光学测量条纹图象的相位分析处理方法中有特殊作用,但在条纹中心分析方法中作用不大.
中值滤波在图像处理中,常用于保护边缘信息,是经典的平滑噪声的方法。
参考博文:https://www.cnblogs.com/qiqibaby/p/5281743.html
代码实现如下
#include "opencv2/imgproc.hpp" #include "opencv2/highgui.hpp" #include<ctime> using namespace cv; using namespace std; //求九个数的中值 uchar Median(uchar n1, uchar n2, uchar n3, uchar n4, uchar n5, uchar n6, uchar n7, uchar n8, uchar n9) { uchar arr[9]; arr[0] = n1; arr[1] = n2; arr[2] = n3; arr[3] = n4; arr[4] = n5; arr[5] = n6; arr[6] = n7; arr[7] = n8; arr[8] = n9; for (int gap = 9 / 2; gap > 0; gap /= 2)//希尔排序 for (int i = gap; i < 9; ++i) for (int j = i - gap; j >= 0 && arr[j] > arr[j + gap]; j -= gap) swap(arr[j], arr[j + gap]); return arr[4];//返回中值 } //图像椒盐化 void salt(Mat &image, int num) { if (!image.data) return;//防止传入空图 int i, j; srand(time(NULL)); for (int x = 0; x < num; ++x) { i = rand() % image.rows; j = rand() % image.cols; image.at<Vec3b>(i, j)[0] = 255; image.at<Vec3b>(i, j)[1] = 255; image.at<Vec3b>(i, j)[2] = 255; } } //中值滤波函数 void MedianFlitering(const Mat &src, Mat &dst) { if (!src.data)return; Mat _dst(src.size(), src.type()); for (int i = 0; i<src.rows; ++i) for (int j = 0; j < src.cols; ++j) { if ((i - 1) > 0 && (i + 1) < src.rows && (j - 1) > 0 && (j + 1) < src.cols) { _dst.at<Vec3b>(i, j)[0] = Median(src.at<Vec3b>(i, j)[0], src.at<Vec3b>(i + 1, j + 1)[0], src.at<Vec3b>(i + 1, j)[0], src.at<Vec3b>(i, j + 1)[0], src.at<Vec3b>(i + 1, j - 1)[0], src.at<Vec3b>(i - 1, j + 1)[0], src.at<Vec3b>(i - 1, j)[0], src.at<Vec3b>(i, j - 1)[0], src.at<Vec3b>(i - 1, j - 1)[0]); _dst.at<Vec3b>(i, j)[1] = Median(src.at<Vec3b>(i, j)[1], src.at<Vec3b>(i + 1, j + 1)[1], src.at<Vec3b>(i + 1, j)[1], src.at<Vec3b>(i, j + 1)[1], src.at<Vec3b>(i + 1, j - 1)[1], src.at<Vec3b>(i - 1, j + 1)[1], src.at<Vec3b>(i - 1, j)[1], src.at<Vec3b>(i, j - 1)[1], src.at<Vec3b>(i - 1, j - 1)[1]); _dst.at<Vec3b>(i, j)[2] = Median(src.at<Vec3b>(i, j)[2], src.at<Vec3b>(i + 1, j + 1)[2], src.at<Vec3b>(i + 1, j)[2], src.at<Vec3b>(i, j + 1)[2], src.at<Vec3b>(i + 1, j - 1)[2], src.at<Vec3b>(i - 1, j + 1)[2], src.at<Vec3b>(i - 1, j)[2], src.at<Vec3b>(i, j - 1)[2], src.at<Vec3b>(i - 1, j - 1)[2]); } else _dst.at<Vec3b>(i, j) = src.at<Vec3b>(i, j); } _dst.copyTo(dst);//拷贝 } void main() { Mat image = imread("E:\\VS2015Opencv\\vs2015\\project\\picture\\06.jpg"); Mat Salt_Image; image.copyTo(Salt_Image); salt(Salt_Image, 3000); Mat image3, image4; MedianFlitering(Salt_Image, image3); medianBlur(Salt_Image, image4, 3); imshow("原图", image); imshow("噪声图", Salt_Image); imshow("自定义中值滤波处理后", image3); imshow("openCV自带的中值滤波", image4); waitKey(); }
也可参考这俩篇博文:https://blog.csdn.net/qq_36359022/article/details/80154900和https://blog.csdn.net/qq_36359022/article/details/80188873
双边滤波(Bilateral filter):
是一种非线性的滤波方法,是结合图像的空间邻近度和像素值相似度的一种折衷处理,同时考虑空域信息和灰度相似性,达到保边去噪的目的。具有简单、非迭代、局部的特点。双边滤波器的好处是可以做边缘保存(edge preserving),一般过去用的维纳滤波或者高斯滤波去降噪,都会较明显地模糊边缘,对于高频细节的保护效果并不明显。
这是网上一般的公式说明,但是感觉理解起来很难,毕竟是数学。根据下图来简要理解一下:
1.图(a)是原始图像,左侧区域是白色(像素值为 255),右侧区域是黑色(像素值为0)
2.图(b)是进行均值滤波的可能结果。在进行均值滤波时,仅仅考虑空间信息,此时左右两侧的像素的处理结果是综合考虑周边元素像素值,并对它们取均值得到的
3.图(c)是进行双边滤波的可能结果。在进行双边滤波时,不仅考虑空间信息,还考虑色彩差别信息
在双边滤波中,在计算左侧白色区域边缘点的滤结果时
1.对于白色的点,给予的权重较大
2.对于黑色的点,由于色彩差异较大,颜色距离很远(注意,不是像素点之间的物理距离,而是颜色值的距离。像素点的值分别是0和 255,差别很大,所以说它们颜色距离很远) 因此可以将它们的权重设置为0。
这样,在计算左侧白色边缘滤波结果时,得到的仍然是白色。因此,双边滤波后,左侧边缘得到保留
在计算右侧黑色区域边缘点的滤波结果时:
1.对于黑色的点,给予的权重较大
2.对于白色的点,由于色彩差异较大,颜色距离很远,因此可以将它们的权重设置为0
这样,在计算右侧黑色边滤波结果时,得到的仍然是黑色。因此,双边滤波后,左侧边缘得到保留
参考链接:https://www.jianshu.com/p/a440eb29c334
具体计算还没理解清楚。以后用到再学吧
下面代码来自博文:https://blog.csdn.net/shan54321/article/details/80658088
#include <opencv2/core/core.hpp> #include <opencv2/highgui/highgui.hpp> #include <opencv2/imgproc/imgproc.hpp> #include <iostream> #include<ctime> using namespace std; using namespace cv; /* 计算空间权值 */ double **get_space_Array(int _size, int channels, double sigmas) { // [1] 空间权值 int i, j; // [1-1] 初始化数组 double **_spaceArray = new double*[_size + 1]; //多一行,最后一行的第一个数据放总值 for (i = 0; i < _size + 1; i++) { _spaceArray[i] = new double[_size + 1]; } // [1-2] 高斯分布计算 int center_i, center_j; center_i = center_j = _size / 2; _spaceArray[_size][0] = 0.0f; // [1-3] 高斯函数 for (i = 0; i < _size; i++) { for (j = 0; j < _size; j++) { _spaceArray[i][j] = exp(-(1.0f)* (((i - center_i)*(i - center_i) + (j - center_j)*(j - center_j)) / (2.0f*sigmas*sigmas))); _spaceArray[_size][0] += _spaceArray[i][j]; } } return _spaceArray; } /* 计算相似度权值 */ double *get_color_Array(int _size, int channels, double sigmar) { // [2] 相似度权值 int n; double *_colorArray = new double[255 * channels + 2]; //最后一位放总值 double wr = 0.0f; _colorArray[255 * channels + 1] = 0.0f; for (n = 0; n < 255 * channels + 1; n++) { _colorArray[n] = exp((-1.0f*(n*n)) / (2.0f*sigmar*sigmar)); _colorArray[255 * channels + 1] += _colorArray[n]; } return _colorArray; } /* 双边 扫描计算 */ void doBialteral(cv::Mat *_src, int N, double *_colorArray, double **_spaceArray) { int _size = (2 * N + 1); cv::Mat temp = (*_src).clone(); // [1] 扫描 for (int i = 0; i < (*_src).rows; i++) { for (int j = 0; j < (*_src).cols; j++) { // [2] 忽略边缘 if (i >(_size / 2) - 1 && j >(_size / 2) - 1 && i < (*_src).rows - (_size / 2) && j < (*_src).cols - (_size / 2)) { // [3] 找到图像输入点,以输入点为中心与核中心对齐 // 核心为中心参考点 卷积算子=>高斯矩阵180度转向计算 // x y 代表卷积核的权值坐标 i j 代表图像输入点坐标 // 卷积算子 (f*g)(i,j) = f(i-k,j-l)g(k,l) f代表图像输入 g代表核 // 带入核参考点 (f*g)(i,j) = f(i-(k-ai), j-(l-aj))g(k,l) ai,aj 核参考点 // 加权求和 注意:核的坐标以左上0,0起点 double sum[3] = { 0.0,0.0,0.0 }; int x, y, values; double space_color_sum = 0.0f; // 注意: 公式后面的点都在核大小的范围里 // 双边公式 g(ij) = (f1*m1 + f2*m2 + ... + fn*mn) / (m1 + m2 + ... + mn) // space_color_sum = (m1 + m12 + ... + mn) for (int k = 0; k < _size; k++) { for (int l = 0; l < _size; l++) { x = i - k + (_size / 2); // 原图x (x,y)是输入点 y = j - l + (_size / 2); // 原图y (i,j)是当前输出点 values = abs((*_src).at<cv::Vec3b>(i, j)[0] + (*_src).at<cv::Vec3b>(i, j)[1] + (*_src).at<cv::Vec3b>(i, j)[2] - (*_src).at<cv::Vec3b>(x, y)[0] - (*_src).at<cv::Vec3b>(x, y)[1] - (*_src).at<cv::Vec3b>(x, y)[2]); space_color_sum += (_colorArray[values] * _spaceArray[k][l]); } } // 计算过程 for (int k = 0; k < _size; k++) { for (int l = 0; l < _size; l++) { x = i - k + (_size / 2); // 原图x (x,y)是输入点 y = j - l + (_size / 2); // 原图y (i,j)是当前输出点 values = abs((*_src).at<cv::Vec3b>(i, j)[0] + (*_src).at<cv::Vec3b>(i, j)[1] + (*_src).at<cv::Vec3b>(i, j)[2] - (*_src).at<cv::Vec3b>(x, y)[0] - (*_src).at<cv::Vec3b>(x, y)[1] - (*_src).at<cv::Vec3b>(x, y)[2]); for (int c = 0; c < 3; c++) { sum[c] += ((*_src).at<cv::Vec3b>(x, y)[c] * _colorArray[values] * _spaceArray[k][l]) / space_color_sum; } } } for (int c = 0; c < 3; c++) { temp.at<cv::Vec3b>(i, j)[c] = sum[c]; } } } } // 放入原图 (*_src) = temp.clone(); return; } /* 双边滤波函数 */ void myBialteralFilter(cv::Mat *src, cv::Mat *dst, int N, double sigmas, double sigmar) { // [1] 初始化 *dst = (*src).clone(); int _size = 2 * N + 1; // [2] 分别计算空间权值和相似度权值 int channels = (*dst).channels(); double *_colorArray = NULL; double **_spaceArray = NULL; _colorArray = get_color_Array(_size, channels, sigmar); _spaceArray = get_space_Array(_size, channels, sigmas); // [3] 滤波 doBialteral(dst, N, _colorArray, _spaceArray); return; } //图像椒盐化 void salt(Mat &image, int num) { if (!image.data) return;//防止传入空图 int i, j; srand(time(NULL)); for (int x = 0; x < num; ++x) { i = rand() % image.rows; j = rand() % image.cols; image.at<Vec3b>(i, j)[0] = 255; image.at<Vec3b>(i, j)[1] = 255; image.at<Vec3b>(i, j)[2] = 255; } } int main(void) { // [1] src读入图片 cv::Mat src = cv::imread("E:\\VS2015Opencv\\vs2015\\project\\picture\\06.jpg"); cv::imshow("原图", src); // [2] dst目标图片 cv::Mat dst1,dst2; // [3] 滤波 N越大越平越模糊(2*N+1) sigmas空间越大越模糊sigmar相似因子 myBialteralFilter(&src, &dst1, 25, 12.5, 50); Mat Salt_Image; src.copyTo(Salt_Image); salt(Salt_Image, 3000); myBialteralFilter(&Salt_Image, &dst2, 25, 12.5, 50); // [4] 窗体显示 cv::imshow("加噪声", Salt_Image); cv::imshow("dst1", dst1); cv::imshow("加噪声dst2", dst2); cv::waitKey(0); cv::destroyAllWindows(); return 0; }
今天的文章图像滤波分享到此就结束了,感谢您的阅读,如果确实帮到您,您可以动动手指转发给其他人。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/48657.html