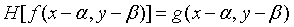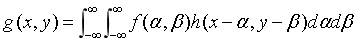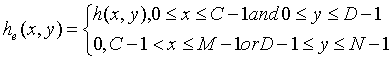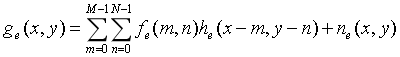图像逆滤波复原_什么是图像滤波

　　图像复原的方法很多，常用的比较经典的是反向滤波法和约束还原法。博主在做反向滤波实验的过程中，发现图像复原的关键是退化模型的建立，可以夸张地说：要有好的复原效果就得根据各个图像的退化特点建立相关的退化模型，并在退化模型的基础上做相关的滤波或者说对待处理的像素做相应的处理，从而尽可能地复原图像。再说一遍，复原方法的关键是退化模型。可以想到的是，由于造成图像退化的原因五花八门。简单的有加性退化、减性、乘性、除性退化等；复杂的有非线性退化等。从这一点看来似乎没有通用的复原方法，这样一来似乎只能使用深度学习等智能算法做一些通用复原算法的研究了。博主推荐在使用神经网络等算法进行研究之前，先修《数据分析与数据挖掘》和《复杂性思维》，或许能从中找到通用复原算法的钥匙！

实验内容　　

　　利用逆滤波和其他逆卷积算法对运动模糊或散焦模糊图像进行图像复原，并给出实现结果。

【背景知识】

1. 图像退化模型

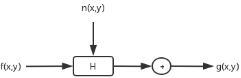
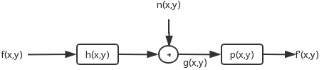
　　图形复原处理的关键是建立退化模型，原图像f(x,y)是通过一个系统H及加入一个外来加性噪声n(x,y)而退化成一幅图像g(x,y)的。

　　这样图像的退化过程的数学表达式就可以写为g(x,y)=H[f(x,y)]+n(x,y)。容易想到图像退化及复原的过程如下：

　　如果系统H满足下面两个式子，那么系统就是线性和空间位置不变的系统。在图像复原处理中，非线性和空间变化的系统的模型虽然更具普遍性和准确性，但它却给处理工作带来巨大的困难，它常常没有解或很难用计算机来处理。实际的成像系统在一定条件下往往可以近似地视为线性和空间不变的系统，因此在图像复原处理中，往往用线性和空间不变的系统模型加以近似地视为线性和空间不变的系统。

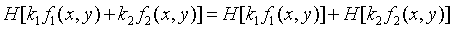
2.连续的退化模型

　　线性系统H可由其冲激响应来表征，当系统H空间位置不变时，则 h(x-α,y-β)=H[δ(x-α,y-β)]。系统H对输入f(x,y)的响应就是系统输入信号f(x,y)与系统冲激响应的卷积。考虑加性噪声n(x,y)时。可写为：

　　其中n(x,y)与图像中位置无关。

3.离散的退化模型

　　如果给出 A×B 大小的数字图像，以及 C×D 大小的点扩散函数，可首先扩展大小为 M×N 的周期延拓图像。

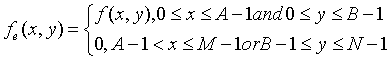
　　为避免折叠，要求 M≥A+C-1，N≥B+D-1。这样一来，f_e(x,y)和h_e(x,y)分别成为二维周期函数，它们在x和y方向上的周期分别为M和N。由此得到二维退化模型为一个二维卷积形式：
　　

　　式中，x=0,1,2,3，…，M-1；y=0,1,2，…，N-1；g_e(x,y)也为周期函数，其周期与f_e(x,y)和h_e(x,y)完全一样。上式也可用矩阵表示为 g=Hf+n。G(u,v)、F(u,v)和N(u,v)分别是g(x,y)、f(x,y)和n(x,y)的二维傅里叶变换。于是有G(u,v)=MNH(u,v)F(u,v)+N(u,v)。这样就将求f(x,y)的过程转换为求解F(u,v)的过程，简化了计算过程，同时上式也是进行图像复原的基础。

图像的复原方法：
反向滤波法

约束还原法

运动模糊图像的复原

模糊模型

水平匀速直线运动引起模糊的复原

　　复原的关键在退化模型的估计，复原的基础建立在退化模型之上。

逆滤波代码如下：

#include <opencv2/highgui.hpp>
#include <opencv2/imgproc.hpp>
#include <iostream>
#define GRAY_THRESH 10

using namespace std;
using namespace cv;

void idfft(Mat complexI, Mat image, int oph, int opw, string str);
void zero_to_center(Mat& freq_plane);

int main()
{
    char imgname[] = "1.png";
    Mat img = imread(imgname, 0);
    if (img.empty()) return 0;
    imshow("srcimg", img);

    string filename = "1.png";
    Mat image = imread(filename, IMREAD_GRAYSCALE); // 灰度图像
    if (image.empty()) return 0;
    imshow("src", image);
    image.convertTo(image, CV_32FC1); // 转换到32位浮点型单通道矩阵

    ///快速傅里叶变换/
    int oph = getOptimalDFTSize(image.rows);
    int opw = getOptimalDFTSize(image.cols);
    Mat padded;
    copyMakeBorder(image, padded, 0, oph - image.rows, 0, opw - image.cols,
        BORDER_CONSTANT, Scalar::all(0)); // 增加边框

    Mat pad_show;
    normalize(padded, pad_show, 0, 1, NORM_MINMAX); //归一化
    imshow("padded", pad_show); // 显示添加了边框的原图

    Mat temp[] = { padded, Mat::zeros(padded.size(),CV_32FC1) }; // 二通道
    Mat complexI;
    merge(temp, 2, complexI); // 合并多个阵列以形成单个多通道阵列
    dft(complexI, complexI);    // 傅里叶变换

    //显示频谱图
    split(complexI, temp);
    zero_to_center(temp[0]);
    zero_to_center(temp[1]);
    Mat aa;
    magnitude(temp[0], temp[1], aa); // 计算计算二维矢量的幅值。dst(I)=sqrt(x(I)^2+y(I)^2)
    divide(aa, oph * opw, aa); // 除法
    imshow("pu", aa);

    merge(temp, 2, complexI);

    /*----------------------------------退化-------------------------------------------------------*/
     // 生成退化函数
    const float ee = 1e-3;
    Mat Degenerate_function(padded.size(), CV_32FC2); // 32位浮点型双通道
    for (int i = 0; i < Degenerate_function.rows; i++) {
        float* dq = Degenerate_function.ptr<float>(i);
        for (int j = 0; j < Degenerate_function.cols; j++) {
            double hmi = -pow(pow(i - oph / 2, 2) + pow(j - opw / 2, 2), 5.0 / 6);
            float mh = exp(hmi) < ee ? ee : exp(hmi);
            dq[2 * j] = mh;
            dq[2 * j + 1] = mh;
        }
    }
    multiply(complexI, Degenerate_function, complexI); // 计算两个数组的每元素缩放乘积。
    Mat ccomplexI = complexI.clone();
    idfft(ccomplexI, image, oph, opw, "退化");

    /*----------------------------------运算部分---------------------------------------------------*/
    // 频域滤波 
    //生成频域滤波核 巴特沃斯低通滤波器 （注：不使用滤波器效果更佳）
    Mat butter_sharpen(padded.size(), CV_32FC2); // 32位浮点型双通道
    double D0 = 50.0;
    int n = 4;
    for (int i = 0; i < butter_sharpen.rows; i++) {
        float* q = butter_sharpen.ptr<float>(i);
        for (int j = 0; j < butter_sharpen.cols; j++) {
            double d = sqrt(pow(i - oph / 2, 2) + pow(j - opw / 2, 2));
            q[2 * j] = 1.0 / (1 + pow(D0 / d, 2 * n));
            q[2 * j + 1] = 1.0 / (1 + pow(D0 / d, 2 * n));
        }
    }

    // 生成退化函数
    Mat Degenerate_function1(padded.size(), CV_32FC2); // 32位浮点型双通道
    float MM = oph * opw;
    for (int i = 0; i < Degenerate_function1.rows; i++) {
        float* dq = Degenerate_function1.ptr<float>(i);
        for (int j = 0; j < Degenerate_function1.cols; j++) {
            double hmi = -pow(pow(i - oph / 2, 2) + pow(j - opw / 2, 2), 5.0 / 6);
            float mh = exp(hmi) * MM < ee ? ee : exp(hmi) * MM;
            dq[2 * j] = mh;
            dq[2 * j + 1] = mh;
        }
    }

    multiply(complexI, butter_sharpen, complexI); // 计算两个数组的每元素缩放乘积。
    divide(complexI, Degenerate_function1, complexI); // 除法

    idfft(complexI, image, oph, opw, "复原");

    waitKey();
    return 0;
}

void idfft(Mat complexI, Mat image, int oph, int opw, string str)
{
    string s1 = "_filter", s2 = "dstSharpen";
    //傅里叶反变换
    idft(complexI, complexI, DFT_INVERSE);

    Mat dstSharpen[2];
    split(complexI, dstSharpen); // 将多通道阵列划分为多个单通道阵列。
    //    magnitude(dstSharpen[0],dstSharpen[1],dstSharpen[0]);  //求幅值(模)
    for (int i = 0; i < oph; i++) {
        float* q = dstSharpen[0].ptr<float>(i);
        for (int j = 0; j < opw; j++) {
            q[j] = q[j] * pow(-1, i + j);
        }
    }
    Mat show;
    //    divide(dstSharpen[0], dstSharpen[0].cols*dstSharpen[0].rows, show);
    normalize(dstSharpen[0], show, 0, 1, NORM_MINMAX); //....
    show = show(Rect(0, 0, image.cols, image.rows));
    imshow(str+s1, show);

    threshold(dstSharpen[0], dstSharpen[0], 0, 255, THRESH_BINARY); // 阈值化
    normalize(dstSharpen[0], dstSharpen[0], 0, 1, NORM_MINMAX); // 映射到0~1
    dstSharpen[0] = dstSharpen[0](Rect(0, 0, image.cols, image.rows));
    imshow(str+s2, dstSharpen[0]);
}

void zero_to_center(Mat& freq_plane)
{
    //    freq_plane = freq_plane(Rect(0, 0, freq_plane.cols & -2, freq_plane.rows & -2));
        //这里为什么&上-2具体查看opencv文档
        //其实是为了把行和列变成偶数 -2的二进制是11111111.......10 最后一位是0
    int cx = freq_plane.cols / 2; int cy = freq_plane.rows / 2;

    //以下的操作是移动图像  (零频移到中心) 与函数center_transform()作用相同，只是一个先处理，一个dft后再变换
    Mat part1_r(freq_plane, Rect(0, 0, cx, cy));  //元素坐标表示为(cx,cy)
    Mat part2_r(freq_plane, Rect(cx, 0, cx, cy));
    Mat part3_r(freq_plane, Rect(0, cy, cx, cy));
    Mat part4_r(freq_plane, Rect(cx, cy, cx, cy));

    Mat tmp;
    part1_r.copyTo(tmp);  //左上与右下交换位置(实部)
    part4_r.copyTo(part1_r);
    tmp.copyTo(part4_r);

    part2_r.copyTo(tmp);  //右上与左下交换位置(实部)
    part3_r.copyTo(part2_r);
    tmp.copyTo(part3_r);
}

Inverse_filtering

#include <iostream>
#include <opencv2/opencv.hpp>
#include <cmath>

using namespace cv;
using namespace std;

void calcPSF(Mat& outputImg, Size filterSize, int len, double theta); // 维纳滤波
void fftshift(const Mat& inputImg, Mat& outputImg); // 频谱平移
void filter2DFreq(const Mat& inputImg, Mat& outputImg, const Mat& H); // 卷积
void calcWnrFilter(const Mat& input_h_PSF, Mat& output_G, double nsr);  // 傅里叶变换
void edgetaper(const Mat& inputImg, Mat& outputImg, double gamma = 5.0, double beta = 0.2); // 减少图像恢复时的振铃效果

int LEN = 50;
int THETA = 360;
int snr = 8000;
Mat imgIn;
Rect roi;
Mat himage;

int main()
{
    string strFileName = "1.png";
    Mat imgIn1 = imread(strFileName, IMREAD_GRAYSCALE);
    imshow("原始图像", imgIn1);

    string strInFileName = "2.png";
    Mat imgIn = imread(strInFileName, IMREAD_GRAYSCALE);
    imshow("退化图像", imgIn);

    Rect roi = Rect(0, 0, imgIn.cols & -2, imgIn.rows & -2); // ***&-2指保留最大的2次幂 ***&11111110
    int D0 = 30; // 截止频率
    int n = 1; // 巴特沃斯滤波系数的分母幂次
    float k = 0.0025; // 退化函数的幂系数 0.001 0.00025
    int rlen = imgIn.rows & -2, clen = imgIn.cols & -2;
    float hf = 1.0 / (rlen * rlen);
    Mat HimgIn(roi.size(), CV_32F, Scalar(0)); // 巴特沃斯低通滤波器
    Mat Himage(roi.size(), CV_32F, Scalar(0)); // 点扩散函数
    for (int i = 0; i < rlen; i++)
    {
        float* himg = HimgIn.ptr<float>(i);
        float* hima = Himage.ptr<float>(i);
        for (int j = 0; j < clen; j++)
        {
            // 巴特沃斯
            float D = sqrt((i - rlen / 2) * (i - rlen / 2) + (j - clen / 2) * (j - clen / 2));
            float hfen = pow((1 + D / D0), 2 * n);
            hfen >= 0 ? hfen : 1e-3;
            // hfen >= 255 ? 255 : hfen;
            himg[j] = 1.0 / hfen;

            // 退化
            float hmi = -k * pow(((i - rlen / 2) * (i - rlen / 2) + (j - clen / 2) * (j - clen / 2)), 5.0 / 6);
            float hhh = 1.0 / exp(hmi) * hf;
            hima[j] = hhh;
        }
    }

    himage = Himage;
    cout << rlen << "\t" << clen << endl;

    Mat outimg, fhimg;
    Mat Gimg = imgIn.clone();
    calcWnrFilter(HimgIn, fhimg, 1.0 / double(snr));
    Gimg.convertTo(Gimg, CV_32F);
    edgetaper(Gimg, Gimg);
    filter2DFreq(Gimg(roi), outimg, fhimg);
    outimg.convertTo(outimg, CV_8U);
    normalize(outimg, outimg, 0, 255, NORM_MINMAX);
    imshow("result", outimg);

    // normalize(fGimg, fGimg, 0, 255, NORM_MINMAX);
    // imshow("频谱", fGimg);

    // cout << pow((1 + 1), 5.0 / 6) << endl;


    Mat imgOut;
    // cout << (3 & -2) << endl;
    // 维纳滤波开始
    /*Mat Hw, h;
    calcPSF(h, roi.size(), LEN, THETA);
    calcWnrFilter(h, Hw, 1.0 / double(snr));

    imgIn.convertTo(imgIn, CV_32F);
    edgetaper(imgIn, imgIn);

    filter2DFreq(imgIn(roi), imgOut, Hw);

    imgOut.convertTo(imgOut, CV_8U);
    normalize(imgOut, imgOut, 0, 255, NORM_MINMAX);
    imshow("result", imgOut);*/

    waitKey();
    return 0;
}

//! [calcPSF]
void calcPSF(Mat& outputImg, Size filterSize, int len, double theta)
{
    Mat h(filterSize, CV_32F, Scalar(0));
    Point point(filterSize.width / 2, filterSize.height / 2);
    ellipse(h, point, Size(0, cvRound(float(len) / 2.0)), 90.0 - theta, 0, 360, Scalar(255), FILLED);
    Scalar summa = sum(h);
    outputImg = h / summa[0];
}
//! [calcPSF]

//! [fftshift]
void fftshift(const Mat& inputImg, Mat& outputImg)
{
    outputImg = inputImg.clone();
    int cx = outputImg.cols / 2;
    int cy = outputImg.rows / 2;
    Mat q0(outputImg, Rect(0, 0, cx, cy));
    Mat q1(outputImg, Rect(cx, 0, cx, cy));
    Mat q2(outputImg, Rect(0, cy, cx, cy));
    Mat q3(outputImg, Rect(cx, cy, cx, cy));
    Mat tmp;
    q0.copyTo(tmp);
    q3.copyTo(q0);
    tmp.copyTo(q3);
    q1.copyTo(tmp);
    q2.copyTo(q1);
    tmp.copyTo(q2);
}
//! [fftshift]

//! [filter2DFreq]
void filter2DFreq(const Mat& inputImg, Mat& outputImg, const Mat& H)
{
    Mat planes[2] = { Mat_<float>(inputImg.clone()), Mat::zeros(inputImg.size(), CV_32F) };
    Mat complexI;
    merge(planes, 2, complexI);
    dft(complexI, complexI, DFT_SCALE); // 二维的

    Mat planesH[2] = { Mat_<float>(H.clone()), Mat::zeros(H.size(), CV_32F) };
    Mat complexH;
    merge(planesH, 2, complexH);
    Mat complexIH;
    mulSpectrums(complexI, complexH, complexIH, 0);

    Mat planesHH[2] = { Mat_<float>(himage.clone()),Mat::zeros(himage.size(),CV_32F) };
    Mat complexHH;
    merge(planesHH, 2, complexHH);
    Mat complexIHH;
    mulSpectrums(complexIH, complexHH, complexIHH, 0);

    complexIHH += Scalar::all(1);                    // switch to logarithmic scale

    log(complexIHH, complexIHH);

    log(complexIHH, complexIHH);

    idft(complexIHH, complexIHH);
    split(complexIHH, planes);
    outputImg = planes[0];

    /*idft(complexIH, complexIH);
    split(complexIH, planes);
    outputImg = planes[0];*/
}
//! [filter2DFreq]

//! [calcWnrFilter]
void calcWnrFilter(const Mat& input_h_PSF, Mat& output_G, double nsr)
{
    Mat h_PSF_shifted;
    fftshift(input_h_PSF, h_PSF_shifted);
    Mat planes[2] = { Mat_<float>(h_PSF_shifted.clone()), Mat::zeros(h_PSF_shifted.size(), CV_32F) };
    Mat complexI;
    merge(planes, 2, complexI);
    dft(complexI, complexI);
    split(complexI, planes);
    Mat denom;
    pow(abs(planes[0]), 2, denom);
    denom += nsr;
    divide(planes[0], denom, output_G);
}
//! [calcWnrFilter]

//! [edgetaper]
void edgetaper(const Mat& inputImg, Mat& outputImg, double gamma, double beta)
{
    int Nx = inputImg.cols;
    int Ny = inputImg.rows;
    Mat w1(1, Nx, CV_32F, Scalar(0));
    Mat w2(Ny, 1, CV_32F, Scalar(0));

    float* p1 = w1.ptr<float>(0);
    float* p2 = w2.ptr<float>(0);
    float dx = float(2.0 * CV_PI / Nx);
    float x = float(-CV_PI);
    for (int i = 0; i < Nx; i++)
    {
        p1[i] = float(0.5 * (tanh((x + gamma / 2) / beta) - tanh((x - gamma / 2) / beta)));
        x += dx;
    }
    float dy = float(2.0 * CV_PI / Ny);
    float y = float(-CV_PI);
    for (int i = 0; i < Ny; i++)
    {
        p2[i] = float(0.5 * (tanh((y + gamma / 2) / beta) - tanh((y - gamma / 2) / beta)));
        y += dy;
    }
    Mat w = w2 * w1;
    multiply(inputImg, w, outputImg);
}
//! [edgetaper]

ImageRestoration

———————————–continue——————————————-

今天的文章图像逆滤波复原_什么是图像滤波分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容，请发送邮件至举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/48998.html

图像逆滤波复原_什么是图像滤波

实验内容

相关推荐

发表回复

实验内容　　